Mezcla de dos cantidades de agua (2)

Enunciado

¿Cómo cambian los resultados del problema “Mezcla de dos cantidades de agua” si las paredes son diatermas?

Solución

En el caso de paredes diatermas el sistema alcanza finalmente el estado de equilibrio térmico con el ambiente, por lo que la temperatura final de cada parte de agua es la misma que la exterior

$T_{1f}=T_{2f}=T_{\mathrm {ext} }=50\circ C=323\,K$

La cantidad de calor que entra en en el agua caliente es

$Q_{1}=mc(T_{1f}-T_{1i})=(0.250\,\mathrm {kg} )\times \left(4.184{\frac {\mathrm {kJ} }{\mathrm {kg} \cdot \mathrm {K} }}\right)\times (-30\,\mathrm {K} )=-31.3\,\mathrm {kJ}$

Es negativo porque en realidad sale. Para el agua fría

$Q_{1}=mc(T_{1f}-T_{1i})=(0.750\,\mathrm {kg} )\times \left(4.184{\frac {\mathrm {kJ} }{\mathrm {kg} \cdot \mathrm {K} }}\right)\times (+30\,\mathrm {K} )=+94.1\,\mathrm {kJ}$

La cantidad neta de calor que entra en el sistema en este caso no es nula

$Q=Q_{1}+Q_{2}=62.7\,\mathrm {kJ}$

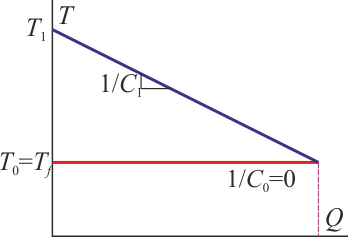
En este caso la gráfica seria la correspondiente a que haya presente un foco térmico, cuya temperatura es constante