|
|
| Línea 57: |
Línea 57: |
| <center><math>\overrightarrow{OA}=-h\vec{\imath}\qquad\qquad \overrightarrow{AB}=h\vec{\imath}</math></center> | | <center><math>\overrightarrow{OA}=-h\vec{\imath}\qquad\qquad \overrightarrow{AB}=h\vec{\imath}</math></center> |
|
| |
|
| <center>[[Archivo:varillas-articuladas-tT/2.png|400px]]</center> | | <center>[[Archivo:varillas-articuladas-tT-2.png|400px]]</center> |
|
| |
|
|
| |
|
Revisión del 23:06 29 dic 2023
Enunciado
Se tiene un sistema articulado formado por dos barras de la misma longitud h situadas sobre una superficie horizontal.
La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular 2Ω.
- En el instante
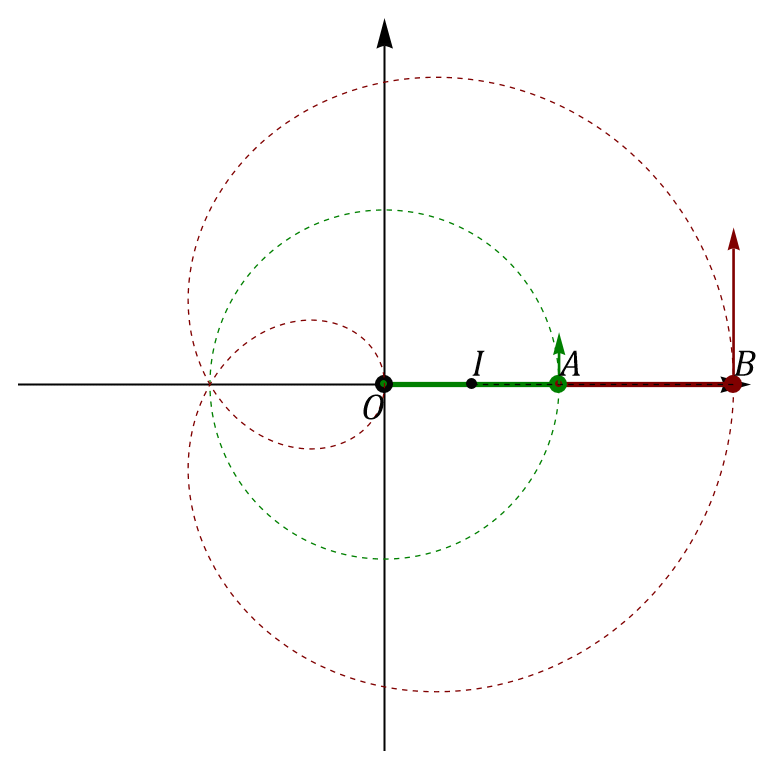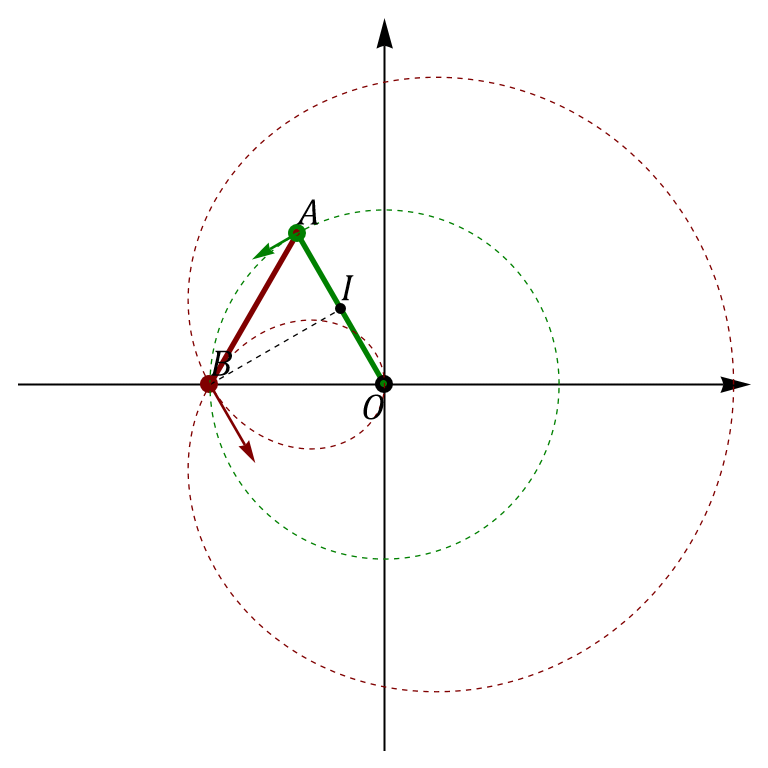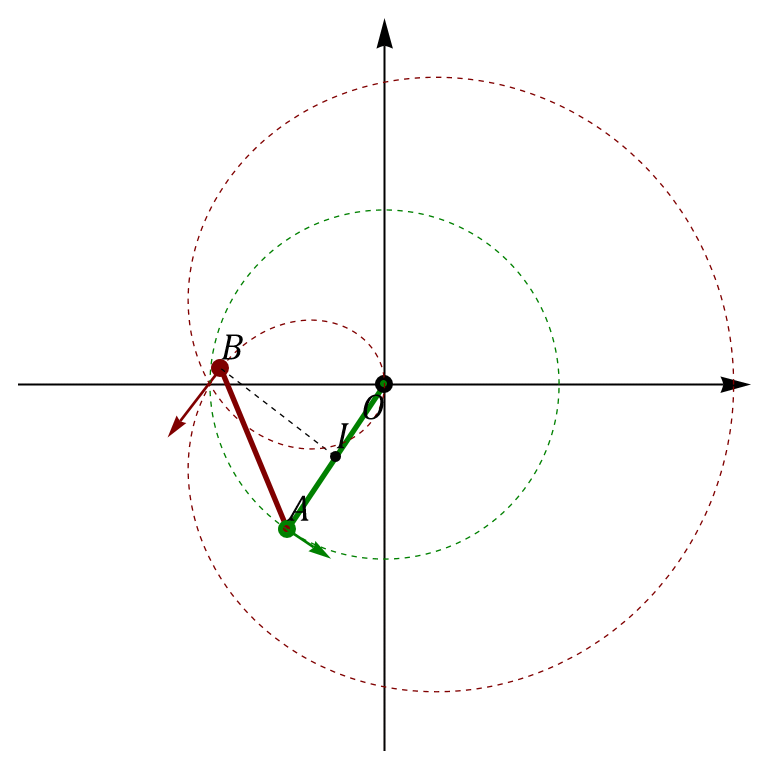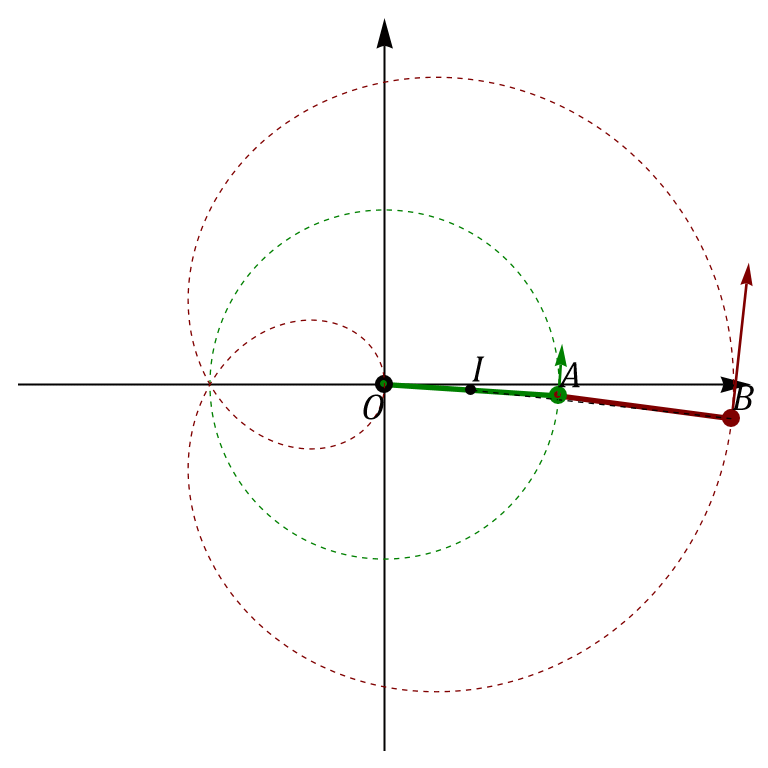
 el sistema está completamente extendido a lo largo del eje
el sistema está completamente extendido a lo largo del eje  . Para este instante
. Para este instante
- Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra.
- Localice la posición del centro instantáneo de rotación del movimiento de la segunda barra respecto a los ejes fijos.
- Halle la aceleración de A y de B.
- Considere ahora el instante
 . Para este instante
. Para este instante
- Determine la posición del extremo B así como la velocidad de este punto en ese instante.
- Determine la posición del CIR de la barra AB en ese momento.
- Halle la aceleración de A y la de B en ese instante.
- Calcule la posición del CIR de la barra AB para cualquier instante t.

Para el instante t = 0
En el instante inicial

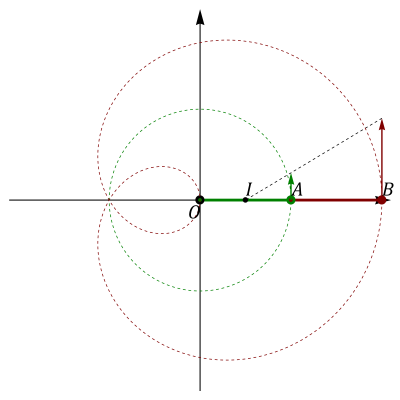
Velocidad de A
El punto A es parte de un sólido que efectúa una rotación alrededor de un eje por O, por lo que

Velocidad de B
B es parte d eun segundo sólido, al cual también pertenece A. Este sólido gira con una velocidad angular diferente y no alrededor de O. Por ello,

Centro instantáneo de rotación
Una vez que tenemos la velocidad de un punto, A, y la velocidad angular, 2Ω, podemos hallar la posición del CIR respecto a este punto.

Esta es la posición respecto al punto A. Respecto al origen de coordenadas será

Es decir, el CIR de la segunda barra se encuentra en el punto medio de la primera. Esto se puede obtener también gráficamente a partir de las velocidades de A y B.
Aceleración de A
La aceleración de A es la correspondiente a un movimiento circular uniforme alrededor de O, con aceleración angular nula

Aceleración de B
De manera similar se calcula la aceleración de B, conocida la aceleración de AB

En el instante t = π/Ω
En este instante la varilla OA ha completado media vuelta, mientras que la AB ha dado una vuelta entera. Esto quiere decir que, en este instante

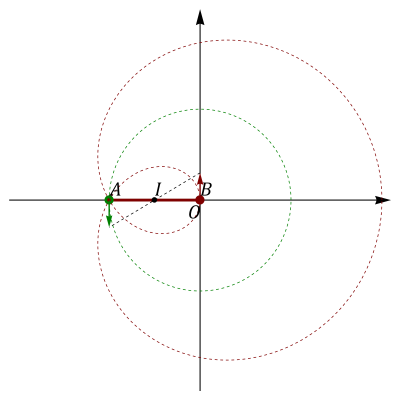
Teniendo esto en cuenta, los nuevos resultados son los siguientes.
Velocidad de A
Ahora es la opuesta a la inicial

Velocidad de B
Para el punto B resulta

Centro instantáneo de rotación
Con la velocidad de un punto, A, y la velocidad angular, 2Ω, podemos hallar la nueva posición del CIR respecto a este punto.

Esta es la posición respecto al punto A. Respecto al origen de coordenadas será

Vemos que sigue estando en el centro de la primera barra. esto también se puede ver gráficamente.
Aceleración de A
La aceleración de A es la correspondiente a un movimiento circular uniforme alrededor de O, con aceleración angular nula

Aceleración de B
De manera similar se calcula la aceleración de B, conocida la aceleración de AB

CIR en cualquier instante
Si consideramos un sistema de vectores de vectores ligado a la primera barra, de manera que  apunta a lo largo de la barra y
apunta a lo largo de la barra y  es ortogonal a ella.
es ortogonal a ella.
En este sistema, la posición de A es, en todo momento

y su velocidad

A partir de aquí obtenemos la posición del CIR respecto a A

y respecto al origen

Vemos que en todo momento se halla en el punto medio de la varilla OA.