Diferencia entre revisiones de «Equilibrio de dos cámaras de aire»
(Página creada con «==Enunciado== Se tiene un sistema formado por dos cámaras de aire seco (γ=1.4). La cámara izquierda (subsistema 1) es rígida. La derecha (subsistema 2) está limitada en su lado derecho por un pistón móvil, siendo la presión externa de 100 kPa. Las paredes exteriores y el pistón son adiabáticos. En el estado inicial, las dos cámaras ocupan 1 litro cada una y la presión de ambas es de 100 kPa, siendo la temperatura de la de la derecha 600 K y la de la…») |
Sin resumen de edición |
||
| (No se muestra una edición intermedia del mismo usuario) | |||
| Línea 23: | Línea 23: | ||
Esto nos da la temperatura final | Esto nos da la temperatura final | ||
<center><math>T_f = \frac{0.833\cdot 300+ 0.583\cdot 600}{0.833+0.583}\mathrm{K}= | <center><math>T_f = \frac{0.833\cdot 300+ 0.583\cdot 600}{0.833+0.583}\mathrm{K}=424\,\mathrm{K}</math></center> | ||
==Trabajo, calor y energía== | |||
===Para la cámara 1=== | |||
====Trabajo==== | |||
Puesto que la cámara 1 es rígida, el trabajo sobre ella es nulo | |||
<center><math>W_1 = 0\,</math></center> | |||
====Variación de energía interna==== | |||
La variación la obtenemos del incremento de temperaturas y es igual al calor que entra en la cámara por ser el proceso a volumen constante. | |||
<center><math>\Delta U_1 = n_1 c_v(T_f-T_1) = 0.833\,\frac{\mathrm{J}}{\mathrm{K}}(424-300)\,\mathrm{K}=103\,\mathrm{J}</math></center> | |||
====Variación de entalpía==== | |||
La variación de entalpía es proporcional a la variación de la energía interna | |||
<center><math>\Delta H_1 = n_1 c_p \,\Delta T= \gamma n_1 c_v \Delta T = \gamma\,\Delta U = 144\,\mathrm{J}</math></center> | |||
====Calor==== | |||
El calor, en este caso, coincide con la variación de la energía interna | |||
<center><math>Q_1=\Delta U_1 - W_1 = 103\,\mathrm{J}</math></center> | |||
===Para la cámara 2=== | |||
====Variación de entalpía==== | |||
La variación de entalpía es igual al calor que entra en la cámara, por ser el proceso a presión constante | |||
<center><math>\Delta H_2 = n_2 c_p \,\Delta T= 0.583\,\frac{\mathrm{J}}{\mathrm{K}}(424-600)\,\mathrm{K}= -103\,\mathrm{J}</math></center> | |||
====Calor==== | |||
El calor, en este caso, coincide con la variación de entalpía | |||
<center><math>Q_2=\Delta H_2 =-103\,\mathrm{J}</math></center> | |||
Este calor es igual y de signo contrario al que entra en la cámara 1, ya que el calor sale de una cámara y va a la otra. | |||
====Variación de energía interna==== | |||
La variación es proporcional a la variación de entalpía | |||
<center><math>\Delta U_2 = n_2 c_v(T_f-T_2) = \frac{1}{\gamma} n_2 c_p(T_f-T_2)=\frac{\Delta H_2}{\gamma}=-73.5\,\mathrm{J}</math></center> | |||
====Trabajo==== | |||
La cámara 1 está a presión constante por lo que podríamos calcular el trabajo como | |||
<center><math>W_2 = -p_2(V_f-V_2)\,</math></center> | |||
hallando previamente el volumen final, pero no nos hace falta porque disponemos de funciones de estado | |||
<center><math>W_2=\Delta U_2 -Q_2=\Delta U_2-\Delta H_2=+29.4\,\mathrm{J}</math></center> | |||
===Sistema completo=== | |||
Para cada una de las magnitudes sumamos los resultados de los dos apartados anteriores: | |||
;Variación de energía interna: | |||
<center><math>\Delta U=\Delta U_1+\Delta U_2=+29.4\,\mathrm{J}</math></center> | |||
;Variación de entalpía: | |||
<center><math>\Delta H=\Delta H_1+\Delta H_2=+41.2,\mathrm{J}</math></center> | |||
;Calor: | |||
<center><math>Q=Q_1+Q_2=0.0\,\mathrm{J}</math></center> | |||
;Trabajo: | |||
<center><math>W=W_1+W_2= +29.4\,\mathrm{J}</math></center> | |||
Revisión actual - 17:32 28 feb 2024
Enunciado
Se tiene un sistema formado por dos cámaras de aire seco (γ=1.4). La cámara izquierda (subsistema 1) es rígida. La derecha (subsistema 2) está limitada en su lado derecho por un pistón móvil, siendo la presión externa de 100 kPa. Las paredes exteriores y el pistón son adiabáticos. En el estado inicial, las dos cámaras ocupan 1 litro cada una y la presión de ambas es de 100 kPa, siendo la temperatura de la de la derecha 600 K y la de la izquierda 300 K, que también es la temperatura exterior. La pared entre las dos cámaras no es un aislante perfecto, sino que lentamente el calor va pasando de la cámara caliente a la fría.
- Calcule la temperatura final de cada una de las dos cámaras.
- Calcule el trabajo neto que entra, el calor neto que entra, la variación de energía interna y de entalpía para cada uno de los dos subsistemas y para el sistema completo.
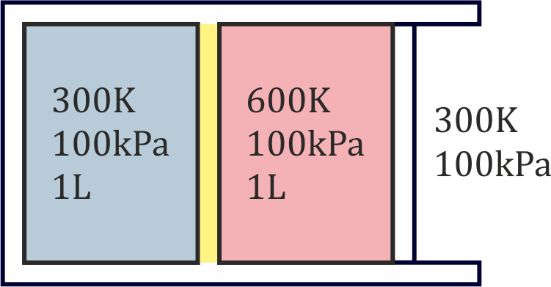
Temperatura final
Tenemos el equilibrio de dos sistemas contenidos en un recipiente adiabático. Por ello la temperatura final es
En este caso, la cámara de la izquierda está a volumen constante, por ser rígida, mientras que la derecha está a presión constante, por tener un émbolo móvil. Por tanto
Podemos hallar los valores de las capacidades caloríficas
Esto nos da la temperatura final
Trabajo, calor y energía
Para la cámara 1
Trabajo
Puesto que la cámara 1 es rígida, el trabajo sobre ella es nulo
Variación de energía interna
La variación la obtenemos del incremento de temperaturas y es igual al calor que entra en la cámara por ser el proceso a volumen constante.
Variación de entalpía
La variación de entalpía es proporcional a la variación de la energía interna
Calor
El calor, en este caso, coincide con la variación de la energía interna
Para la cámara 2
Variación de entalpía
La variación de entalpía es igual al calor que entra en la cámara, por ser el proceso a presión constante
Calor
El calor, en este caso, coincide con la variación de entalpía
Este calor es igual y de signo contrario al que entra en la cámara 1, ya que el calor sale de una cámara y va a la otra.
Variación de energía interna
La variación es proporcional a la variación de entalpía
Trabajo
La cámara 1 está a presión constante por lo que podríamos calcular el trabajo como
hallando previamente el volumen final, pero no nos hace falta porque disponemos de funciones de estado
Sistema completo
Para cada una de las magnitudes sumamos los resultados de los dos apartados anteriores:
- Variación de energía interna
- Variación de entalpía
- Calor
- Trabajo

















