Diferencia entre revisiones de «Anilla ensartada en un aro giratorio»
(Página creada con «==Anilla ensartada en un aro giratorio== Una pequeña anilla de masa m está ensartada en un aro vertical de radio ''R'' que puede girar alrededor del eje ''OZ'' (este sistema equivale a un péndulo simple formado por una masa ''m'' unida a una varilla rígida de longitud ''R'', unida por su otro extremo a un punto fijo O mediante una articulación esférica). La masa está sometida a la acción del peso. <center>Archivo:anilla-aro-giratorio.png</center> # Consi…») |
|||
| (No se muestran 9 ediciones intermedias del mismo usuario) | |||
| Línea 14: | Línea 14: | ||
==Oscilaciones verticales== | ==Oscilaciones verticales== | ||
Suponemos en primer lugar que el aro vertical se encuentra en una posición fija. Construimos un sistema de referencia <math>OX_2Y_2Z_2</math> ligado a este aro (la razón de que lo llamemos “2&” y no “1&” es que más tarde nos hará falta el sistema “1&”), con el eje <math>OZ_2</math> en la dirección vertical, el eje <math>OY_2</math> la horizontal contenida en el plano del aro y el <math>OX_2</math> el eje del aro (perpendicular a él). El origen de coordenadas, que va a ser el mismo en todo el problema. | |||
En este sistema la fuerza del peso es | |||
<center><math>\vec{F}_g=-mgk\vec{k}_2</math></center> | |||
Para la anilla consideramos un segundo sistema de referencia “3&”, que comparte el eje OX con el 2, y que tiene a la anilla situada en <math>OZ_3</math> negativo. Este sistema está girado un ángulo θ alrededor de <math>OX_2=OX_3</math> respecto al sistema 2 | |||
La relación entre las dos bases es | |||
<center><math> | |||
\begin{array}{rcl} | |||
\vec{\imath}_3&=&\vec{\imath}_2\\ | |||
\vec{\jmath}_3&=&\cos(\theta)\vec{\jmath}_2 + \mathrm{sen}(\theta)\vec{k}_2\\ | |||
\vec{k}_3&=&-\mathrm{sen}(\theta)\vec{\jmath}_2 + \cos(\theta)\vec{k}_2 | |||
\end{array}</math></center> | |||
La velocidad angular con la que gira el sistema de referencia 3 (que será con la que gire la anilla alrededor del centro del aro) vale | |||
<center><math>\vec{\omega}_{32}=\dot{\theta}\vec{\imath}_2=\dot{\theta}\vec{\imath}_3</math></center> | |||
y la aceleración angular | |||
<center><math>\vec{\alpha}_{32}=\ddot{\theta}\vec{\imath}_2=\ddot{\theta}\vec{\imath}_3</math></center> | |||
La posición de la anilla (partícula P) es fija en el sistema 3 | |||
<center><math>\overrightarrow{OP}=-R\vec{k}_3</math></center> | |||
Su velocidad es la de un movimiento de rotación alrededor del centro del aro | |||
<center><math>\vec{v}^P_{32}=\vec{\omega}_{32}\times\overrightarrow{OP}=\left(\dot{\theta}\vec{\imath}_3\right)\times \left(-R\vec{k}_3\right)=\dot{\theta}R\vec{\jmath}_3</math></center> | |||
y su aceleración es | |||
<center><math>\vec{a}^P_{32}=\vec{\alpha}_{32}\times\overrightarrow{OP}+\vec{\omega}_{32}\times\left(\vec{\omega}_{32}\times\overrightarrow{OP}\right)</math></center> | |||
con | |||
<center><math>\vec{\alpha}_{32}\times\overrightarrow{OP} = \left(\ddot{\theta}\vec{\imath}_3\right)\times \left(-R\vec{k}_3\right)=\ddot{\theta}R\vec{\jmath}_3</math></center> | |||
y | |||
<center><math>\vec{\omega}_{32}\times\left(\vec{\omega}_{32}\times\overrightarrow{OP}\right)=\left(\dot{\theta}\vec{\imath}_3\right)\times\left(\dot{\theta}R\vec{\jmath}_3\right)=R\dot{\theta}^2\vec{k}_{3}</math></center> | |||
lo que nos da la aceleración | |||
<center><math>\vec{a}^P_{32}=R\ddot{\theta}\vec{\jmath}_3+R\dot{\theta}^2\vec{k}_3</math></center> | |||
De acuerdo con la segunda ley de Newton esta aceleración es proporcional a la fuerza aplicada, que es suma del peso y de la reacción normal del aro. | |||
<center><math>m\vec{a}^P_{32}=m\vec{g}+\vec{F}_n</math></center> | |||
Escribimos la expresión vectorial de cada fuerza. El peso va en la dirección vertical (la de <math>\vec{k}_2</math>) hacia abajo, y la reacción va en la dirección radial (la de <math>\vec{k}_3</math>). | |||
<center><math>m\left(R\ddot{\theta}\vec{\jmath}_3+R\dot{\theta}^2\vec{k}_3\right)=-mg\vec{k}_2+F_n\vec{k}_3</math></center> | |||
Si no estamos interesados en hallar la reacción del aro, podemos eliminarla multiplicando escalarmente por <math>\vec{\jmath}_3</math>, que es ortogonal a esa dirección. Aplicando que | |||
<center><math>\vec{\jmath}_3\cdot\vec{\jmath}_{3}=1\qquad\qquad \vec{\jmath}_3\cdot\vec{k}_{3}=0\qquad\qquad \vec{\jmath}_3\cdot\vec{k}_{2}=\mathrm{sen}(\theta)</math></center> | |||
queda finalmente | |||
<center><math>mR\ddot{\theta}=-mg\,\mathrm{sen}(\theta)</math></center> | |||
o, simplificando | |||
<center><math>\ddot{\theta}=-\frac{g}{R}\,\mathrm{sen}(\theta)</math></center> | |||
Esta es la conocida como ecuación del péndulo. | |||
===Equilibrio y estabilidad=== | |||
Los puntos de equilibrio son aquellos en los que cuando se deja la anilla con velocidad inicial nula permanecen en la misma posición indefinidamente. Para que ello ocurra, la aceleración debe ser atmbién nula. | |||
<center><math>\ddot{\theta}=0\qquad\Rightarrow\qquad \mathrm{sen}(\theta_\mathrm{eq})=0\qquad\Rightarrow\qquad \theta_\mathrm{eq}=\left\{\begin{matrix}0 \\ \pi\end{matrix}\right.</math></center> | |||
Los únicos puntos de equilibrio son el inferior y el superior. | |||
Para ver su estabilidad debemos analizar qué ocurre en las proximidades de las posiciones de equilibrio. | |||
Para θ próximo a 0, podemos hacer la aproximación | |||
<center><math>\mathrm{sen}(\theta)\simeq \theta</math></center> | |||
y la ecuación de movimiento se reduce a | |||
<center><math>\ddot{\theta}=-\frac{g}{R}\theta</math></center> | |||
Esta es la ecuación del oscilador armónico. Sus soluciones son oscilaciones alrededor de la posición de equilibrio, con frecuencia <math>\omega=\sqrt{g/R}</math>. Este punto de equilibrio es estable, pues la aceleración tiende a devolver la masa a su posición central. | |||
Para <math>\theta_\mathrm{eq}=\pi</math> hacemos un desarrollo en serie de Taylor alrededor de este punto. | |||
<center><math>\theta=\pi+\delta\ (\delta\ll 1)\qquad\qquad \ddot{\theta}=\ddot{\delta}</math></center> | |||
<center><math>\mathrm{sen}(\theta)=\,\mathrm{sen}(\pi+\delta)\simeq\,\mathrm{sen}(\pi)+\delta\cos(\pi) = -\delta</math></center> | |||
Esto nos da la ecuación | |||
<center><math>\ddot{\delta}=+\frac{g}{R}\delta</math></center> | |||
Esta ecuación tiene por soluciones exponenciales reales, una de las cuales tiene un exponente positivo, esto quiere decir que en cuanto separamos la anilla un poco de la posición de equilibrio superior, esta resbala y se aleja de este punto. El equilibrio es inestable. | |||
==Giro alrededor de un eje vertical== | ==Giro alrededor de un eje vertical== | ||
==Movimiento general== | ==Movimiento general== | ||
===Mediante fuerzas ficticias=== | ===Mediante fuerzas ficticias=== | ||
Cuando consideramos el movimiento general, podemos seguir empleando el sistema de referencia “2&” siempre que tengamos en cuenta que este sistema está girando respecto a un sistema de referencia inercial fijo “1&” y por tanto es preciso introducir las fuerzas ficticias correspondientes. | |||
La velocidad angular con la que gira el aro respecto al sistema inercial es | |||
<center><math>\vec{\omega}_{21}=\dot{\phi}\vec{k}_1=\dot{\phi}\vec{k}_2</math></center> | |||
y su aceleración angular | |||
<center><math>\vec{\alpha}_{21}=\ddot{\phi}\vec{k}_1=\ddot{\phi}\vec{k}_2</math></center> | |||
===Mediante el teorema de Coriolis=== | ===Mediante el teorema de Coriolis=== | ||
==Giro forzado== | ==Giro forzado== | ||
===Puntos de equilibrio=== | ===Puntos de equilibrio=== | ||
===Estabilidad=== | ===Estabilidad=== | ||
Revisión actual - 20:18 30 nov 2023
Anilla ensartada en un aro giratorio
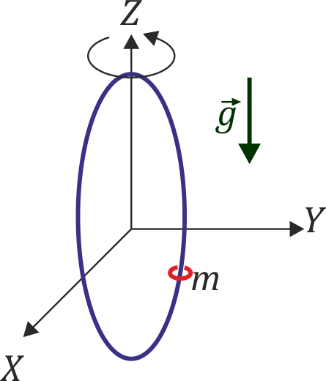
Una pequeña anilla de masa m está ensartada en un aro vertical de radio R que puede girar alrededor del eje OZ (este sistema equivale a un péndulo simple formado por una masa m unida a una varilla rígida de longitud R, unida por su otro extremo a un punto fijo O mediante una articulación esférica). La masa está sometida a la acción del peso.
- Considere, en primer lugar, el movimiento en un plano vertical. Determine la ecuación de movimiento para el ángulo θ que la anilla forma con la vertical. ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
- Considere el caso de que el aro gira con velocidad angular constante alrededor del eje vertical. ¿Cuál debe ser la relación entre Ω y el ángulo con la vertical, θ, para que la anilla ni suba ni baje en el aro, describiendo una circunferencia horizontal? ¿Puede conseguirse un movimiento circular sea cual sea Ω?
- Suponga ahora el movimiento general, en el cual puede cambiar tanto θ como el ángulo ϕ, de giro alrededor del eje vertical. A partir de la 2ª ley de Newton, obtenga las ecuaciones de movimiento para estos dos ángulos. Esto puede hacerse de diferentes maneras:
- Empleando un sistema de referencia en rotación alrededor del eje vertical, y empleando las fuerzas ficticias necesarias.
- Considerando una composición de movimientos mediante tres sistemas de referencia: uno fijo “1”, uno intermedio “2” que gira alrededor del eje vertical un ángulo ϕ y uno ligado “3” que gira respecto a un eje horizontal un ángulo θ.
- Considerando el caso general, con movimiento en las dos coordenadas ϕ y θ, suponga que con un motor se fuerza a una rotación constante . En ese caso, ¿cómo queda la ecuación para θ? ¿Qué puntos de equilibrio hay? ¿Son estables o inestables?
Oscilaciones verticales
Suponemos en primer lugar que el aro vertical se encuentra en una posición fija. Construimos un sistema de referencia ligado a este aro (la razón de que lo llamemos “2&” y no “1&” es que más tarde nos hará falta el sistema “1&”), con el eje en la dirección vertical, el eje la horizontal contenida en el plano del aro y el el eje del aro (perpendicular a él). El origen de coordenadas, que va a ser el mismo en todo el problema.
En este sistema la fuerza del peso es
Para la anilla consideramos un segundo sistema de referencia “3&”, que comparte el eje OX con el 2, y que tiene a la anilla situada en negativo. Este sistema está girado un ángulo θ alrededor de respecto al sistema 2
La relación entre las dos bases es
La velocidad angular con la que gira el sistema de referencia 3 (que será con la que gire la anilla alrededor del centro del aro) vale
y la aceleración angular
La posición de la anilla (partícula P) es fija en el sistema 3
Su velocidad es la de un movimiento de rotación alrededor del centro del aro
y su aceleración es
con
y
lo que nos da la aceleración
De acuerdo con la segunda ley de Newton esta aceleración es proporcional a la fuerza aplicada, que es suma del peso y de la reacción normal del aro.
Escribimos la expresión vectorial de cada fuerza. El peso va en la dirección vertical (la de ) hacia abajo, y la reacción va en la dirección radial (la de ).
Si no estamos interesados en hallar la reacción del aro, podemos eliminarla multiplicando escalarmente por , que es ortogonal a esa dirección. Aplicando que
queda finalmente
o, simplificando
Esta es la conocida como ecuación del péndulo.
Equilibrio y estabilidad
Los puntos de equilibrio son aquellos en los que cuando se deja la anilla con velocidad inicial nula permanecen en la misma posición indefinidamente. Para que ello ocurra, la aceleración debe ser atmbién nula.
Los únicos puntos de equilibrio son el inferior y el superior. Para ver su estabilidad debemos analizar qué ocurre en las proximidades de las posiciones de equilibrio.
Para θ próximo a 0, podemos hacer la aproximación
y la ecuación de movimiento se reduce a
Esta es la ecuación del oscilador armónico. Sus soluciones son oscilaciones alrededor de la posición de equilibrio, con frecuencia . Este punto de equilibrio es estable, pues la aceleración tiende a devolver la masa a su posición central.
Para hacemos un desarrollo en serie de Taylor alrededor de este punto.
Esto nos da la ecuación
Esta ecuación tiene por soluciones exponenciales reales, una de las cuales tiene un exponente positivo, esto quiere decir que en cuanto separamos la anilla un poco de la posición de equilibrio superior, esta resbala y se aleja de este punto. El equilibrio es inestable.
Giro alrededor de un eje vertical
Movimiento general
Mediante fuerzas ficticias
Cuando consideramos el movimiento general, podemos seguir empleando el sistema de referencia “2&” siempre que tengamos en cuenta que este sistema está girando respecto a un sistema de referencia inercial fijo “1&” y por tanto es preciso introducir las fuerzas ficticias correspondientes.
La velocidad angular con la que gira el aro respecto al sistema inercial es
y su aceleración angular


































