Diferencia entre revisiones de «Masa que cuelga de dos hilos oblicuos»
(Página creada con «==Enunciado== Un peso de 16.8 N cuelga del techo suspendido de dos hilos situados como indica la figura. Calcule la tensión de cada hilo. <center>400px</center> ==Solución==») |
Sin resumen de edición |
||
| Línea 4: | Línea 4: | ||
<center>[[Archivo:masa-dos-hilos-oblicuos.png|400px]]</center> | <center>[[Archivo:masa-dos-hilos-oblicuos.png|400px]]</center> | ||
==Solución== | ==Solución== | ||
Puesto que la masa está en equilibrio, su aceleración es nula. La suma de las fuerzas que actúan sobre ella es nula: | |||
<center><math>m\vec{g}+\vec{F}_{T1}+\vec{F}_{T2}=\vec{0}</math></center> | |||
Tomando un sistema de ejes en el que el eje OX es horizontal y el OY es vertical y hacia arriba, estas fuerzas quedan en la forma | |||
<center><math>m\vec{g}=-mg\vec{\jmath}\qquad\qquad \vec{F}_{T1}=-F_{T1}\,\mathrm{sen}(\alpha)\vec{\imath}+F_{T1}\cos(\alpha)\vec{\jmath}\qquad\qquad \vec{F}_{T2}=F_{T2}\,\mathrm{sen}(\beta)\vec{\imath}+F_{T2}\cos(\beta)\vec{\jmath}</math></center> | |||
donde α y β son los ángulos que cada hilo forma con la vertical. | |||
Para hallar estas razones trigonométricas empleamos geometría. Trazamos la vertical por la masa, que medirá una longitud h hasta el techo. Esta altura divide el lado superior en dos tramos de longitudes a y b. Entonces, tenemos, en cm, | |||
<center><math>a + b = 70\qquad\qquad a^2+h^2 = 65^2 \qquad\qquad b^2+h^2 = 75^2</math></center> | |||
Restamos la segunda de la tercera | |||
<center><math>b^2 - a^2 = 75^2 - 65^2 \qquad\Rightarrow\qquad (b+a)(b-a)=(75+65)(75-65)</math></center> | |||
Sustituimos aquí la primera de las tres ecuaciones y nos queda | |||
<center><math>70(b-a) = 140\cdot 10 \qquad\Rightarrow\qquad b - a= 20</math></center> | |||
Por tanto, el sistema se reduce a | |||
<center><math>b + a = 70\qquad\qquad b-a = 20 \qquad\Rightarrow\qquad b = 45\,\mathrm{cm},\ a=25\,\mathrm{cm},\ h = 60\,\mathrm{cm}</math></center> | |||
lo que nos da las razones trigonométricas | |||
<center><math>\mathrm{sen}(\alpha)=\frac{25}{65}=\frac{5}{13}\qquad \cos(\alpha)=\frac{60}{65}=\frac{12}{13}\qquad\qquad \mathrm{sen}(\beta)=\frac{45}{75}=\frac{3}{5}\qquad \cos(\beta)=\frac{60}{75}=\frac{4}{5}</math></center> | |||
Llevamos esto al equilibrio de fuerzas | |||
<center><math>\begin{array}{rcccl} | |||
x:&\quad &0&=& -\dfrac{5}{13}F_{T1}+\dfrac{3}{5}F_{T2}\\ | |||
y:&\quad &0&=& -16.8+\dfrac{12}{13}F_{T1}+\dfrac{4}{5}F_{T2} | |||
\end{array}</math></center> | |||
La solución de este sistema da | |||
<center><math>F_{T1}=11.7\,\mathrm{N}\qquad \qquad F_{T2}=7.5\,\mathrm{N}</math></center> | |||
y, en forma vectorial, | |||
<center><math>\vec{F}_{T1}=(-4.5\vec{\imath}+10.8\vec{\jmath})\,\mathrm{N}\qquad\qquad \vec{F}_{T2}=(4.5\vec{\imath}+6.0\vec{\jmath})\,\mathrm{N}</math></center> | |||
Revisión actual - 14:06 9 nov 2023
Enunciado
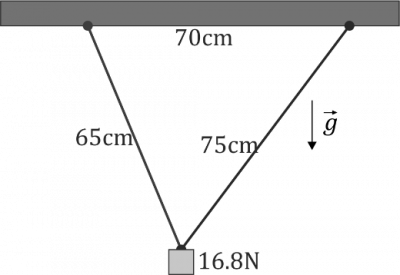
Un peso de 16.8 N cuelga del techo suspendido de dos hilos situados como indica la figura. Calcule la tensión de cada hilo.
Solución
Puesto que la masa está en equilibrio, su aceleración es nula. La suma de las fuerzas que actúan sobre ella es nula:
Tomando un sistema de ejes en el que el eje OX es horizontal y el OY es vertical y hacia arriba, estas fuerzas quedan en la forma
donde α y β son los ángulos que cada hilo forma con la vertical.
Para hallar estas razones trigonométricas empleamos geometría. Trazamos la vertical por la masa, que medirá una longitud h hasta el techo. Esta altura divide el lado superior en dos tramos de longitudes a y b. Entonces, tenemos, en cm,
Restamos la segunda de la tercera
Sustituimos aquí la primera de las tres ecuaciones y nos queda
Por tanto, el sistema se reduce a
lo que nos da las razones trigonométricas
Llevamos esto al equilibrio de fuerzas
La solución de este sistema da
y, en forma vectorial,









