Mezcla de dos cantidades de agua (4)

Enunciado

Se pone en contacto 1 kg de agua a 80 ℃ con una masa m de agua a 20 ℃. ¿Cuál es la temperatura final de la mezcla, en función de m? ¿Cuánto calor entra en la masa m? ¿A qué tienden los resultados si $m\to \infty$?

Solución

Este problema es una generalización del problema “Mezcla de dos cantidades de agua”. Tenemos dos masas de agua que se ponen en contacto. La temperatura final de equilibrio es

$T_{f}={\frac {C_{1}T_{1}+C_{2}T_{2}}{C_{1}+C_{2}}}$

siendo las capacidades caloríficas proporcionales a la masa de cada parte

$T_{f}={\frac {m_{1}cT_{1}+m_{2}cT_{2}}{m_{1}c+m_{2}c}}={\frac {m_{1}T_{1}+mT_{2}}{m_{1}+m}}$

Sustituimos los valores numéricos. Podemos escribir la temperatura en grados celsius y la masa en kilogramos. En este caso queda

$T_{f}={\frac {80+20m}{1+m}}$

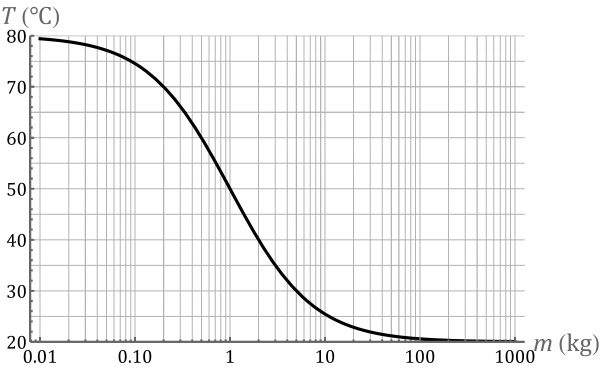
Esta función va de 80 ℃ (para $m=0$) a 20 ℃ (para $m\to \infty$). Cuando mayor es la masa del agua fría menos se ve afectada por el añadido de agua caliente. Para una masa de 10 kg la temperatura final es de 25.45 ℃, para $m=100\,\mathrm {kg}$ es 20.59 ℃ y para $m=1000\,\mathrm {kg}$ es de 20.06 ℃. Esto quiere decir que si vertemos un litro de agua caliente en un metro cúbico de agua fría (mil veces más masa), la temperatura del agua fría casi no cambia y se puede considerar un baño térmico.

Esto se ve claramente en una gráfica con una escala logarítmica, que permite representar varios órdenes de magnitud.

El calor que entra en el sistema es

$Q=m_{1}c(T_{f}-T_{1})=m_{1}c\left({\frac {m_{1}T_{1}+mT_{2}}{m_{1}+m}}-T_{1}\right)={\frac {m_{1}mc(T_{2}-T_{1})}{m_{1}+m}}$

Sustituimos los valores numéricos y queda

$Q={\frac {4.18m(-60)}{1+m}}=-{\frac {250.8m}{1+m}}\,\mathrm {kJ}$