Caso de fuerza dependiente de la posición

Enunciado

Una partícula de masa 2 kg se mueve por el eje OX de forma que cuando pasa por $x=0$ su velocidad es +3 m/s. Sobre la partícula actúa una fuerza en la dirección del mismo eje, ${\vec {F}}=F(x){\vec {\imath }}$ cuya gráfica es la de la figura.

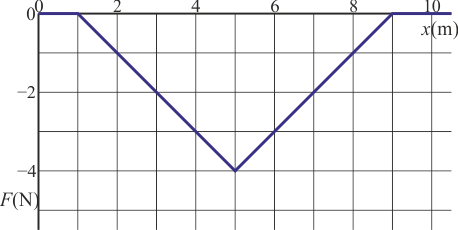
(a)	(b)

1. ¿Cuál es la velocidad de la partícula cuando pasa por $x=10\,\mathrm {m}$?
2. ¿Cuál será la respuesta a la pregunta anterior si la fuerza es la de la gráfica (b)?
3. ¿Cómo es, en cada caso, la gráfica de la energía potencial, si U(0)=0?

Primer caso

El teorema trabajo-energía cinética establece que

$\Delta K=W\,$

En este caso, empleando el SI para todas las variables

$\Delta K={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{i}^{2}={\frac {1}{2}}2v_{f}^{2}-{\frac {1}{2}}2(3)^{2}=v_{f}^{2}-9\qquad (J)$

mientras que el trabajo es igual a la integral

$W=\int F\,\mathrm {d} x=16\,J$

El valor de la integral corresponde al área bajo la curva, que en este caso es igual a la de un triángulo.

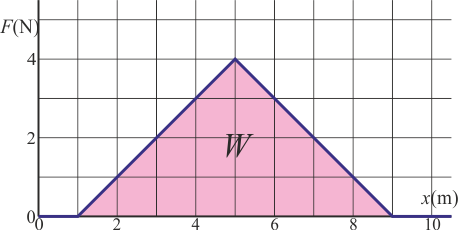
Este trabajo es positivo, como corresponde a que la fuerza vaya en el mismo sentido del movimiento y acelere la partícula.

Igualando las dos cantidades

$v_{f}^{2}-9=16\qquad \Rightarrow \qquad v_{f}^{2}=25\qquad \Rightarrow \qquad v_{f}=5\,{\frac {\mathrm {m} }{\mathrm {s} }}$

Segundo caso

Aplicando el teorema trabajo-energía cinética tenemos que

$\Delta K=W\qquad \Rightarrow \qquad K(B)-K(A)=\int _{A}^{B}F\,\mathrm {d} x$

La energía cinética inicial vale

$K(A)={\frac {1}{2}}mv_{i}^{2}={\frac {1}{2}}2\cdot 3^{2}\mathrm {J} =9\,\mathrm {J}$

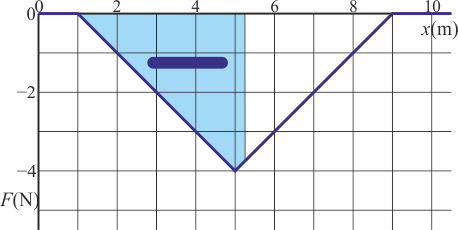
y el trabajo que se realiza sobre la partícula si recorre toda la distancia es el área entre la curva y el eje. Esta integral es negativa en este caso porque la fuerza lo es. Es decir, puesto que la fuerza es negativa se opone al movimiento de la partícula y reduce su energía cinética

$W=\int _{A}^{B}F\,\mathrm {d} x=-16\,\mathrm {J}$

Por tanto, la energía cinética final sería

$K(B)=9\,\mathrm {J} -16\,\mathrm {J} =-7\,\mathrm {J}$

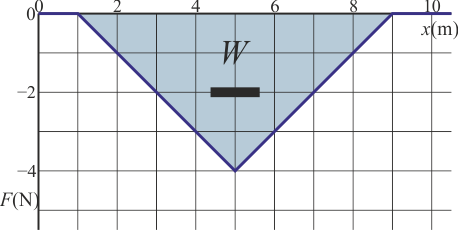
lo cual es imposible, ya que la energía cinética nunca puede ser negativa. Lo que ocurre realmente es que, al ser la fuerza opuesta al movimiento, llega un momento en que la detiene del todo y le da la vuelta. La partícula nunca llega a $x=10\,\mathrm {m}$. El punto de retorno se dará en el momento en que el área entre la curva y el eje llegue a -9J.