Diferencia entre las páginas «Archivo:F1 GIC Disco apoyado en barra fuerzas.png» y «Varilla colgando de cuerda, Enero 2015 (G.I.C.)»
Sin resumen de edición |
(Página creada con «== Enunciado == right Una barra homogénea de masa <math>M</math> y longitud <math>L</math> está apoyada en el suelo y sujeta por una cuerda como se indica en la figura. El ángulo entre la cuerda y la barra es <math>\pi/2</math>. El contacto entre la barra y el suelo es rugoso, con un coeficiente de rozamiento estático <math>\mu</math>. El peso de la barra se aplica en su centro de masas. El ángulo que fo…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | |||
[[Imagen:F1_GIC_Varilla_colgando_de_cuerda_enunciado.png|right]] | |||
Una barra homogénea de masa <math>M</math> y longitud <math>L</math> está apoyada en el suelo y sujeta por una cuerda como se indica en la figura. El ángulo entre | |||
la cuerda y la barra es <math>\pi/2</math>. El contacto entre la barra y el suelo es rugoso, con un coeficiente de rozamiento estático <math>\mu</math>. El peso de la barra se aplica en su centro de masas. El ángulo que forma la barra con el suelo es <math>\alpha</math>. | |||
# En situación de equilibrio estático, calcula la tensión en la cuerda | |||
# Calcula la componente normal de la fuerza sobre la barra en el punto <math>O</math>. | |||
# Fijado el valor de <math>\alpha</math>, ¿qué condición debe cumplir el coeficiente de rozamiento estático para que la barra no deslice en el punto <math>O</math>? | |||
== Solución == | |||
[[Imagen:F1_GIC_Varilla_colgando_de_cuerda_fuerzas.png|right]] | |||
La figura de la derecha muestra las fuerzas que actúan sobre la varilla: su peso, la tensión de la cuerda (dirigida a lo largo de la cuerda) y las fuerzas en el punto <math>O </math>: la componente normal y la tangencial de rozamiento. En el sistema de ejes de la figura estos vectores se escriben | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{P} = -Mg\,\vec{\jmath}\\ | |||
\vec{T}^A = -T\,\mathrm{sen}\,\alpha\,\vec{\imath} + T\cos\alpha\,\vec{\jmath}\\ | |||
\vec{N}^O = N^O\,\vec{\jmath}\\ | |||
\vec{F}_r^O = F_r^O\,\vec{\imath} | |||
\end{array} | |||
</math> | |||
</center> | |||
Las condiciones de equilibrio son que la suma de fuerzas debe ser cero y que el momento neto respecto a un punto debe ser cero. De la primera condición obtenemos | |||
<center> | |||
<math> | |||
\vec{P} + | |||
\vec{T} + | |||
\vec{N}^O + | |||
\vec{F}_r^O = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{ll} | |||
(X): F_r^O = T\,\mathrm{sen}\,\alpha\\ | |||
(Y): N^O + T\cos\alpha = Mg | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Calculamos los momentos respecto al punto <math>O </math>. De este modo nos quedará una ecuación para <math>T </math>. Tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\overrightarrow{OG}\times\vec{P} = | |||
\dfrac{1}{2}\left(L\cos\alpha\,\vec{\imath} + L\,\mathrm{sen}\,\alpha\,\vec{\jmath}\right)\times (-Mg\,\vec{\jmath}) = -\dfrac{1}{2}MgL\cos\alpha\,\vec{k} | |||
\\ | |||
\overrightarrow{OA}\times\vec{T} = | |||
\left(L\cos\alpha\,\vec{\imath} + L\,\mathrm{sen}\,\alpha\,\vec{\jmath}\right)\times \left(-T\,\mathrm{sen}\,\alpha\,\vec{\imath} + T\cos\alpha\,\vec{\jmath}\right) = TL\,\vec{k} | |||
\end{array} | |||
</math> | |||
</center> | |||
La suma de los dos momentos debe ser nula, de donde obtenemos | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}Mg\cos\alpha | |||
</math> | |||
</center> | |||
Obtenemos así las tres fuerzas | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
T = \dfrac{1}{2}Mg\cos\alpha\\ | |||
\\ | |||
F_r^O = \dfrac{1}{2}Mg\cos\alpha\,\mathrm{sen}\,\alpha\\ | |||
\\ | |||
N^O = Mg\,\left(1-\dfrac{1}{2}\cos^2\alpha\right) | |||
\end{array} | |||
</math> | |||
</center> | |||
El equilibrio puede romperse por deslizamiento en el suelo. La condición para que esto no ocurra es | |||
<center> | |||
<math> | |||
|\vec{F}^O_r|\leq|\vec{N}^O| | |||
\Longrightarrow | |||
\mu \geq \dfrac{\cos\alpha\,\mathrm{sen}\,\alpha}{2-\cos^2\alpha} | |||
</math> | |||
</center> | |||
[[Categoría: Problemas de Estática del Sólido Rígido]] | |||
[[Categoría:Problemas de examen]] | |||
[[Categoría:Problemas de examen de F1 GIC]] | |||
Revisión actual - 10:21 3 nov 2023
Enunciado
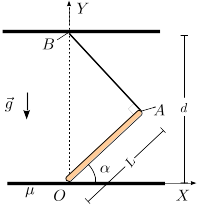
Una barra homogénea de masa y longitud está apoyada en el suelo y sujeta por una cuerda como se indica en la figura. El ángulo entre la cuerda y la barra es . El contacto entre la barra y el suelo es rugoso, con un coeficiente de rozamiento estático . El peso de la barra se aplica en su centro de masas. El ángulo que forma la barra con el suelo es .
- En situación de equilibrio estático, calcula la tensión en la cuerda
- Calcula la componente normal de la fuerza sobre la barra en el punto .
- Fijado el valor de , ¿qué condición debe cumplir el coeficiente de rozamiento estático para que la barra no deslice en el punto ?
Solución
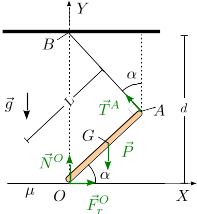
La figura de la derecha muestra las fuerzas que actúan sobre la varilla: su peso, la tensión de la cuerda (dirigida a lo largo de la cuerda) y las fuerzas en el punto : la componente normal y la tangencial de rozamiento. En el sistema de ejes de la figura estos vectores se escriben
Las condiciones de equilibrio son que la suma de fuerzas debe ser cero y que el momento neto respecto a un punto debe ser cero. De la primera condición obtenemos
Calculamos los momentos respecto al punto . De este modo nos quedará una ecuación para . Tenemos
La suma de los dos momentos debe ser nula, de donde obtenemos
Obtenemos así las tres fuerzas
El equilibrio puede romperse por deslizamiento en el suelo. La condición para que esto no ocurra es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 10:20 3 nov 2023 |  | 196 × 209 (14 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:












