(Página creada con «= Partícula moviéndose sobre una parábola = Una partícula se mueve siguiendo la trayectoria descrita por la curva de ecuaciones implícitas <math>y=A(1-x^2/A^2)</math> y <math>z=0</math>, donde <math>A</math> es una constante. La coordenada <math>x</math> varía en el intervalo <math>x\in[0,A]</math>. #Determina el vector tangente en función de la posición de la partícula #Suponiendo que e…»)
 
(Página creada con «= Disco apoyado sobre pared y varilla = right Un disco homogéneo y rígido de radio <math>R</math> y peso <math>P</math> está apoyado en una barra rígida de longitud <math>R</math> y peso <math>P</math>, como se indica en la figura. La prolongación de la recta definida por la barra pasa por el centro del disco. El contacto es liso en la pared vertica…»)
 
Línea 1: Línea 1:
=[[Partícula moviéndose sobre una parábola, Noviembre 2014 (G.I.C.)| Partícula moviéndose sobre una parábola]] =
=[[Disco apoyado sobre pared y varilla, Enero 2015 (G.I.C.)| Disco apoyado sobre pared y varilla]] =
[[Imagen:F1_GIC_Disco_apoyado_en_barra_enunciado.png|right]]
Un disco homogéneo y rígido de radio <math>R</math> y peso <math>P</math> está apoyado en una barra rígida de longitud <math>R</math> y peso <math>P</math>, como se indica en la figura. La prolongación de la recta definida por la barra pasa por el centro del disco. El contacto es liso en la pared vertical, y rugoso entre la barra  y el suelo,  con coeficiente de rozamiento estático <math>\mu</math>. El peso del disco se aplica en su centro (<math>C</math>), y el de la barra en su punto medio (<math>E</math>). En condiciones de equilibrio estático se pide
#La fuerza normal sobre la barra en el punto <math>B</math>.
#La fuerza sobre el disco en el punto <math>A</math>.
#¿Qué condición debe cumplir el ángulo <math>\alpha</math> para que el equilibrio sea posible?


Una partícula se mueve siguiendo la trayectoria descrita por la curva de
=[[Varilla colgando de cuerda, Enero 2015 (G.I.C.)|Varilla colgando de cuerda]] =
ecuaciones implícitas <math>y=A(1-x^2/A^2)</math> y <math>z=0</math>, donde <math>A</math> es una constante. La
[[Imagen:F1_GIC_Varilla_colgando_de_cuerda_enunciado.png|right]]
coordenada <math>x</math> varía en el intervalo <math>x\in[0,A]</math>.
Una barra homogénea de masa <math>M</math> y longitud <math>L</math> está apoyada en el suelo y sujeta por una cuerda como se indica en la figura. El ángulo entre
#Determina el vector tangente en función de la posición de la partícula
la cuerda y la barra es <math>\pi/2</math>. El contacto entre la barra y el suelo es rugoso, con un coeficiente de rozamiento estático <math>\mu</math>. El peso de la barra se aplica en su centro de masas. El ángulo que forma la barra con el suelo es <math>\alpha</math>.  
#Suponiendo que en <math> t=0</math> la distancia recorrida es <math>s=0 </math> encuentra la expresión que da la distancia total recorrida sobre la curva.
# En situación de equilibrio estático, calcula la tensión en la cuerda
#¿Cuál es el vector normal a la trayectoria en <math>x=0 </math>?
# Calcula la componente normal de la fuerza sobre la barra en el punto <math>O</math>.
# Fijado el valor de <math>\alpha</math>, ¿qué condición debe cumplir el coeficiente de rozamiento estático para que la barra no deslice en el punto <math>O</math>?


=[[Partícula con curvatura y aceleración tangencial dependientes del tiempo, Noviembre 2014 (G.I.C.)| Partícula con curvatura y aceleración tangencial dependientes del tiempo]]=
=[[Disco girando sujeto por un muelle, Enero 2015 (G.I.C.)| Disco girando sujeto por un muelle]] =
Una partícula se mueve de modo que, en todo instante, su curvatura es <math>\kappa = At</math> y su aceleración tangencial es <math>a_T=Bt</math>, siendo <math>A</math> y <math>B</math> constantes. Suponemos que en el instante inicial la partícula está en reposo.
[[Imagen:F1_GIC_disco_girando_con_muelle.png|right]]
#¿Cuáles son las unidades base de las constantes en el SI?
Un disco homógeneo de masa <math>M</math> y radio <math>R</math> puede girar en torno al punto <math>O</math> de su borde. El extremo superior del disco está unido al punto <math>A</math> con un resorte ideal de longitud natural nula y constante elástica <math>k</math>. En el instante inicial se encuentra en posición vertical, de modo que el punto <math>B</math> del disco coincide con el punto <math>A</math> donde está anclado el resorte. En <math>t=0</math> empieza a girar hacia la derecha, de modo que su velocidad angular inicial es 0.
#Suponiendo que en <math>t=0</math> se tiene <math>s=0</math>, calcula la distancia recorrida en cada instante de tiempo
# Sabiendo que el momento de inercia del disco respecto a un eje perpendicular a su plano que pasa por su centro es <math>MR^2/2</math>, determina el momento de inercia respecto a un eje perpendicular a su plano que pasa por el punto <math>O</math>.
#Calcula el módulo de la aceleración en cada instante.
#Calcula la velocidad del centro del disco <math>C</math> en el instante en el que está sobre el eje <math>X</math>.


=[[Partícula con dos muelles apoyada sobre un plano vertical, Noviembre 2014 (G.I.C.)| Partícula con dos muelles apoyada sobre un plano vertical]]=
=[[Resorte con rozamiento, Enero 2015 (G.I.C.)| Resorte con rozamiento]] =
[[Imagen:GIC_muelles_plano_vertical_enunciado_PPC_2014.png|right]]
Se tiene un resorte ideal horizontal con constante elástica <math>k=224\,\mathrm{N/m}</math>. Se le engancha una masa <math>m=500\,\mathrm{g}</math>, de modo que oscila sobre una superficie horizontal sin rozamiento.
Un partícula de masa <math>m</math> reposa sin rozamiento sobre un plano vertical definido por los puntos <math>A</math> y <math>B</math> de la figura. Está atada a dos muelles de constantes  elásticas <math>k_1</math> y <math>k_2</math> y longitud natural nula, anclados en los puntos <math>O</math> y <math>C</math>, respectivamente. La partícula no puede deplazarse a lo largo del eje <math>OZ</math>. El plano <math>AB</math> puede desplazarse a lo largo del eje <math>OX</math> de modo que se mantiene siempre vertical.
#¿Cuál es la frecuencia natural de oscilación de la masa, aproximadamente?
#Dibuja el diagrama de cuerpo libre de la partícula.
#Se sumergen tres copias idénticas de este sistema en tres líquidos diferentes, de modo que actúa una fuerza de rozamiento <math>\vec{F}_R = -b_i\vec{v}</math> sobre cada masa. En cada líquido el coeficiente de rozamiento es <math>b_1=10.6\,\mathrm{kg/s}</math>, <math>b_2=21.2\,\mathrm{kg/s}</math>, <math>b_3=42.4\,\mathrm{kg/s}</math>. Clasifica los líquidos, en orden creciente de eficiencia de frenado (primero el que es más eficiente).
#¿Que condición debe cumplirse para que el punto de equilibrio de la masa esté sobre el eje <math>OX</math>
#¿Qué condición  debe cumplir <math>x_P</math> para que el plano <math>AB</math> ejerza una fuerza sobre la partícula?
#Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático <math>\mu_e</math>. Si <math>y_m</math> es la coordenada de la partícula sobre el eje <math>OY</math>, calcula el módulo de la fuerza de rozamiento.
#En la situación con rozamiento, supongamos que <math>k_1=k_2=k</math>, <math>mg=2kd</math>, <math>d=l</math> y <math>x_P=l/4</math>. ¿Cuál es el rango de posiciones de equilibrio de la partícula sobre el plano?


=[[Masas deslizando sobre un plano horizontal, Noviembre 2014 (G.I.C.)| Masas deslizando sobre un plano horizontal]]=
=[[Partícula recorriendo una espiral, Enero 2015 (G.I.C.)| Partícula recorriendo una espiral]] =
[[Imagen:GIC_masas_deslizando_enunciado_PPC_2014.png|right]]
Una partícula de masa <math>m</math> describe una espiral plana con un vector de posición en coordenadas polares <math>\vec{r}(t) = r_0\,e^{\theta(t)}\,\vec{u}_r</math>, siendo <math>\theta(t)=\omega t</math>. Tanto <math>r_0</math> como <math>\omega</math> son constantes.
Las dos masas de la derecha se mueven horizontalmente. El contacto de la masa
#Calcula el momento cinético de la partícula respecto del origen.
<math>M</math> sobre el suelo es liso, mientras que el contacto entre las dos masas es
#Calcula el momento respecto del origen de la fuerza neta que actúa sobre la partícula.
rugoso con un coeficiente de rozamiento estático <math>\mu</math>. Una fuerza
<math>\vec{F}</math> horizontal actúa sobre la masa <math>M</math>.
#Si durante el movimiento las dos masas mantienen su posición relativa, ¿cuál es su aceleración?
#Calcula la fuerza total que la masa <math>m </math> ejerce sobre la masa <math>M </math>.
#¿Qué condición debe cumplir <math>|\vec{F}|</math> para que la masa <math>m</math> no deslice respecto de la masa <math>M</math>?

Revisión actual - 19:47 2 nov 2023

Disco apoyado sobre pared y varilla

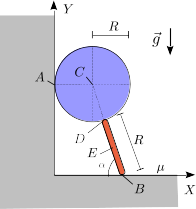
Un disco homogéneo y rígido de radio y peso está apoyado en una barra rígida de longitud y peso , como se indica en la figura. La prolongación de la recta definida por la barra pasa por el centro del disco. El contacto es liso en la pared vertical, y rugoso entre la barra y el suelo, con coeficiente de rozamiento estático . El peso del disco se aplica en su centro (), y el de la barra en su punto medio (). En condiciones de equilibrio estático se pide

  1. La fuerza normal sobre la barra en el punto .
  2. La fuerza sobre el disco en el punto .
  3. ¿Qué condición debe cumplir el ángulo para que el equilibrio sea posible?

Varilla colgando de cuerda

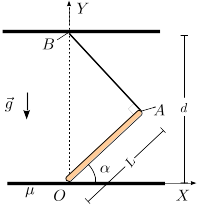
Una barra homogénea de masa y longitud está apoyada en el suelo y sujeta por una cuerda como se indica en la figura. El ángulo entre la cuerda y la barra es . El contacto entre la barra y el suelo es rugoso, con un coeficiente de rozamiento estático . El peso de la barra se aplica en su centro de masas. El ángulo que forma la barra con el suelo es .

  1. En situación de equilibrio estático, calcula la tensión en la cuerda
  2. Calcula la componente normal de la fuerza sobre la barra en el punto .
  3. Fijado el valor de , ¿qué condición debe cumplir el coeficiente de rozamiento estático para que la barra no deslice en el punto ?

Disco girando sujeto por un muelle

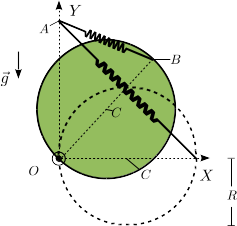
Un disco homógeneo de masa y radio puede girar en torno al punto de su borde. El extremo superior del disco está unido al punto con un resorte ideal de longitud natural nula y constante elástica . En el instante inicial se encuentra en posición vertical, de modo que el punto del disco coincide con el punto donde está anclado el resorte. En empieza a girar hacia la derecha, de modo que su velocidad angular inicial es 0.

  1. Sabiendo que el momento de inercia del disco respecto a un eje perpendicular a su plano que pasa por su centro es , determina el momento de inercia respecto a un eje perpendicular a su plano que pasa por el punto .
  2. Calcula la velocidad del centro del disco en el instante en el que está sobre el eje .

Resorte con rozamiento

Se tiene un resorte ideal horizontal con constante elástica . Se le engancha una masa , de modo que oscila sobre una superficie horizontal sin rozamiento.

  1. ¿Cuál es la frecuencia natural de oscilación de la masa, aproximadamente?
  2. Se sumergen tres copias idénticas de este sistema en tres líquidos diferentes, de modo que actúa una fuerza de rozamiento sobre cada masa. En cada líquido el coeficiente de rozamiento es , , . Clasifica los líquidos, en orden creciente de eficiencia de frenado (primero el que es más eficiente).

Partícula recorriendo una espiral

Una partícula de masa describe una espiral plana con un vector de posición en coordenadas polares , siendo . Tanto como son constantes.

  1. Calcula el momento cinético de la partícula respecto del origen.
  2. Calcula el momento respecto del origen de la fuerza neta que actúa sobre la partícula.
Obtenido de «http://laplace.us.es/wiki/index.php?title=Primera_Prueba_de_Control_2014/15_(G.I.C.)&oldid=1300»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Primera_Prueba_de_Control_2014/15_(G.I.C.)&oldid=1300»