(Página creada con «== Enunciado == Una partícula de masa <math>m</math> describe una espiral plana con un vector de posición en coordenadas polares <math>\vec{r}(t) = r_0\,e^{\theta(t)}\,\vec{u}_r</math>, siendo <math>\theta(t)=\omega t</math>. Tanto <math>r_0</math> como <math>\omega</math> son constantes. #Calcula el momento cinético de la partícula respecto del origen. #Calcula el momento respecto del origen de la fuerza neta que actúa sobre la partícula. == Solución == ===…»)
 
(Página creada con «= Partícula sobre espiral con muelle = right Una partícula de masa <math>m</math> está engarzada en la barra ranurada de la figura. El muelle, de longitud natural <math>l_0<L</math> y constante elástica <math>k</math>, la empuja de modo que, al girar la barra, la partícula está obligada a moverse sobre la espiral indicada, de ecuación <math>r(\t…»)
 
Línea 1: Línea 1:
== Enunciado ==
=[[Partícula sobre espiral con muelle, Enero 2015 (G.I.C.)| Partícula sobre espiral con muelle]] =
Una partícula de masa <math>m</math> describe una espiral plana con un vector de posición en coordenadas polares <math>\vec{r}(t) = r_0\,e^{\theta(t)}\,\vec{u}_r</math>, siendo <math>\theta(t)=\omega t</math>. Tanto <math>r_0</math> como <math>\omega</math> son constantes.
[[Imagen:F1_GIC_particula_espiral_muelle_enunciado.png|right]]
#Calcula el momento cinético de la partícula respecto del origen.
Una partícula de masa <math>m</math> está engarzada en la barra ranurada de la figura. El muelle, de longitud natural <math>l_0<L</math> y constante elástica <math>k</math>, la empuja de modo que, al girar la barra, la partícula está obligada a moverse sobre la espiral indicada, de ecuación <math>r(\theta) = r_0e^{\theta}</math>, con <math>\theta=\theta(t)</math>. La barra gira de modo que la partícula se mueve con rapidez constante <math>v_0</math>. El efecto de la gravedad es despreciable.
#Calcula el momento respecto del origen de la fuerza neta que actúa sobre la partícula.
#Usando coordenadas polares, escribe las expresiones del vector de posición, velocidad y aceleración de la partícula. Deja el resultado en función de <math>\theta</math> y sus derivadas.
#Calcula la ley horaria <math>\theta(t)</math>.
#Determina la fuerza que ejerce el muelle sobre la partícula, asi como la energía potencial del muelle. Expresa estos dos resultados en función del ángulo <math>\theta</math>.
#¿Se conserva la energía mecánica de la partícula? ¿Y el momento cinético respecto a <math>O</math>? Razona las respuestas.


== Solución ==
=[[Barra apoyada en un escalón, Enero 2015 (G.I.C.)| Barra apoyada en un escalón]] =
 
[[Imagen:F1_GIC_barra_apoyada_en_escalon_enunciado.png|right]]
=== Momento cinético ===
Una barra homogénea, de longitud <math>L</math> y peso <math>P</math>, está apoyada sobre un escalón de altura <math>d</math> formando un ángulo <math>\alpha</math> con la horizontal. El contacto en el punto <math>B</math> es liso, mientras que es rugoso en el punto <math>A</math>, con un coeficiente de rozamiento estático <math>\mu</math>.
El vector de posición de la partícula es, en polares:
#Dibuja el diagrama de cuerpo libre de la barra.
<center>
#Determina la expresión de las fuerzas que actúan sobre la barra en condiciones de equilibrio estático.
<math>
#Si <math>\alpha=\pi/4</math>, qué condición debe cumplir <math>d</math> para que se mantenga el equilibrio? ¿El equilibrio se rompe por deslizamiento o por vuelco? Razona la respuesta.
\vec{r} = r_0e^{\theta(t)}\,\vec{u}_r
</math>
</center>
Derivamos respecto al tiempo para obtener la velocidad
<center>
<math>
\vec{v} = r_0\dot{\theta}e^{\theta}\,\vec{u}_r + r_0e^{\theta}\dot{\vec{u}}_r
=
r_0\dot{\theta}e^{\theta}\,(\vec{u}_r + \vec{u}_{\theta})
=
r_0\omega e^{\omega t}\,(\vec{u}_r + \vec{u}_{\theta})
</math>
</center>
Hemos usado que <math>\theta=\omega t </math> y <math>\dot{\theta}=\omega </math>
 
El momento cinético respecto del origen es
<center>
<math>
\vec{L}_O = \vec{r}\times(m\vec{v}) = m\omega r_0^2e^{2\omega t}\,\vec{k}
</math>
</center>
 
=== Momento de la fuerza neta ===
El teorema del momento cinético dice
<center>
<math>
\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} = \vec{M}_O
</math>
</center>
siendo <math>\vec{M}_O </math> el momento de la fuerza neta respecto del punto <math>O </math>. Derivando en la expresión del apartado anterior tenemos
<center>
<math>
\vec{M}_O = 2m\omega^2r_0^2e^{2\omega t}\,\vec{k}
</math>
</center>
 
 
[[Categoría:Dinámica del punto material|1]]
[[Categoría:Problemas de examen]]
[[Categoría:Problemas de examen de F1 GIC]]

Revisión actual - 10:23 3 nov 2023

Partícula sobre espiral con muelle

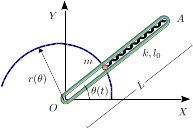
Una partícula de masa está engarzada en la barra ranurada de la figura. El muelle, de longitud natural y constante elástica , la empuja de modo que, al girar la barra, la partícula está obligada a moverse sobre la espiral indicada, de ecuación , con . La barra gira de modo que la partícula se mueve con rapidez constante . El efecto de la gravedad es despreciable.

  1. Usando coordenadas polares, escribe las expresiones del vector de posición, velocidad y aceleración de la partícula. Deja el resultado en función de y sus derivadas.
  2. Calcula la ley horaria .
  3. Determina la fuerza que ejerce el muelle sobre la partícula, asi como la energía potencial del muelle. Expresa estos dos resultados en función del ángulo .
  4. ¿Se conserva la energía mecánica de la partícula? ¿Y el momento cinético respecto a ? Razona las respuestas.

Barra apoyada en un escalón

Una barra homogénea, de longitud y peso , está apoyada sobre un escalón de altura formando un ángulo con la horizontal. El contacto en el punto es liso, mientras que es rugoso en el punto , con un coeficiente de rozamiento estático .

  1. Dibuja el diagrama de cuerpo libre de la barra.
  2. Determina la expresión de las fuerzas que actúan sobre la barra en condiciones de equilibrio estático.
  3. Si , qué condición debe cumplir para que se mantenga el equilibrio? ¿El equilibrio se rompe por deslizamiento o por vuelco? Razona la respuesta.
Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_recorriendo_una_espiral,_Enero_2015_(G.I.C.)&oldid=1311»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_recorriendo_una_espiral,_Enero_2015_(G.I.C.)&oldid=1311»