Diferencia entre las páginas «Archivo:F1 GIA ventiladores vectores.png» y «Disco deslizando sobre hilo rotante, Noviembre 2015 (MR G.I.C.)»
Secciones
Sin resumen de edición |
(Página creada con «== Enunciado == right Un hilo rígido (sólido "0") de longitud <math>L</math> rota alrededor del eje <math>OZ_1</math> con velocidad angular constante <math>\Omega_0</math>, de modo que el punto <math>A</math> está fijo y el punto <math>B</math> describe una circunferencia sobre el plano <math>OX_1Y_1</math>. El hilo forma un ángulo <math>\pi/4</math> con el plano <math>OX_1Y_1</math>. Un disco plano de masa <math>m</m…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | |||
[[Imagen:MR_disco_hilo_rotante_enunciado.png|right]] | |||
Un hilo rígido (sólido "0") de longitud <math>L</math> rota alrededor del eje <math>OZ_1</math> con velocidad angular constante <math>\Omega_0</math>, de modo que el punto <math>A</math> está fijo y el punto <math>B</math> describe una circunferencia sobre el plano <math>OX_1Y_1</math>. El hilo forma un ángulo <math>\pi/4</math> con el plano <math>OX_1Y_1</math>. Un disco plano de masa <math>m</math> y radio <math>R</math> desliza por el hilo a la vez que rota alrededor de él con velocidad angular constante <math>\omega_0</math>. En el instante inicial el centro del disco estaba en el punto <math>A</math>. Se escoge un sólido "0" de modo que el plano <math>OX_0Z_0</math> contiene siempre al hilo. El sistema "2", solidario con el disco, se escoge de modo que el eje <math>GZ_2</math> coincide con su eje de simetría y el eje <math>GY_2</math> es paralelo al eje <math>OY_0</math>. El punto <math>G</math> del disco se mueve sobre el hilo con rapidez uniforme <math>v_0</math>, como se indica en la figura. | |||
#Calcula <math>\vec{\omega}_{21}</math> y <math>\vec{\alpha}_{21}</math>. | |||
#Calcula la velocidad absoluta del centro del disco en el instante inicial. | |||
#¿Qué condición tiene que cumplirse para que el movimiento {21} sea una rotación pura en el instante inicial? | |||
#Supongamos que <math>\omega_0=0</math>. En este caso, el momento cinético del disco respecto de su centro de masas y su energía cinética en el instante en el que el punto <math>G</math> está en el punto <math>B</math>. | |||
== Solución == | |||
=== Cálculo de <math>\vec{\omega}_{21}</math> y <math>\vec{\alpha}_{21}</math>=== | |||
==== Movimiento {01} ==== | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \Omega_0\,\vec{k}_0, | |||
\qquad\qquad | |||
\vec{v}^{\,O}_{01} =\vec{0}. | |||
</math> | |||
</center> | |||
La derivada temporal es | |||
<center> | |||
<math> | |||
\vec{\alpha}_{01} = \vec{0}, | |||
\qquad\qquad | |||
\vec{a}^{\,O}_{01} =\vec{0}. | |||
</math> | |||
</center> | |||
==== Movimiento {20} ==== | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{20} = \omega_0\,\vec{k}_2 | |||
\qquad\qquad | |||
\vec{v}_{20} =-v_0\,\vec{k}_2 | |||
</math> | |||
</center> | |||
La derivada temporal es | |||
<center> | |||
<math> | |||
\vec{\alpha}_{20} = \vec{0}, | |||
\qquad\qquad | |||
\vec{a}_{20} =\vec{0}. | |||
</math> | |||
</center> | |||
No ponemos letra en la velocidad y aceleración pues es una traslación. | |||
==== Movimiento {21} ==== | |||
Usando la composición {21}={20} + {01} tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = | |||
\Omega_0\,\vec{k}_0 + \omega_0\,\vec{k}_2 | |||
</math> | |||
</center> | |||
Expresamos el vector <math>\vec{k}_2</math> en la base "0" | |||
<center> | |||
<math> | |||
\vec{k}_2 = -\dfrac{1}{\sqrt{2}}\,\vec{\imath}_0 + \dfrac{1}{\sqrt{2}}\,\vec{k}_0 | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = -\dfrac{\omega_0}{\sqrt{2}}\,\vec{\imath}_0 + | |||
\left(\Omega_0 + \dfrac{\omega_0}{\sqrt{2}}\right)\,\vec{k}_0. | |||
</math> | |||
</center> | |||
También tenemos | |||
<center> | |||
<math> | |||
\vec{\alpha}_{21} = \vec{\alpha}_{20} +\vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} | |||
= | |||
-\dfrac{1}{\sqrt{2}}\,\omega_0\Omega_0\,\vec{\jmath}_0. | |||
</math> | |||
</center> | |||
Nótese que aunque {20} y {01} son dos rotaciones con aceleración angular nula, su composición tiene aceleración angular no nula. | |||
=== Velocidad del centro del disco en el instante inicial === | |||
Usando la misma composición | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01}. | |||
</math> | |||
</center> | |||
En el instante inicial el punto <math>G</math> está en el eje de giro del movimiento {01}, en el punto <math>A</math>. Por tanto | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{01}(t=0) = \vec{v}^{\,G} + \vec{\omega}_{01}\times\overrightarrow{OA} = \vec{0}. | |||
</math> | |||
</center> | |||
El primer sumando es cero pues <math>\vec{v}^{\,O}_{01}=\vec{0}</math>, y el segundo también pues <math>\vec{\omega}_{01}</math> y <math>\overrightarrow{OA}</math> son paralelos. Entonces | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{21}(t=0) = \vec{v}^{\,G}_{20} = -v_0\,\vec{k}_2 = \dfrac{v_0}{\sqrt{2}}\,\left(\vec{\imath}_0 - \vec{k}_0\right). | |||
</math> | |||
</center> | |||
=== Condición para que el movimiento {21} sea una rotación pura en el instante inicial === | |||
La condición que debe cumplirse es, que en ese instante, el invariante escalar del movimiento sea nulo, es decir | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{21}\cdot\vec{\omega}_{21}=0 | |||
\Longrightarrow | |||
\sqrt{2}\,\omega_0 + \Omega_0 = 0. | |||
</math> | |||
</center> | |||
=== Cálculo del momento angular y la energía cinética === | |||
Con la condición <math>\omega_0=0</math> tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = \Omega_0\,\vec{k}_0 = | |||
\dfrac{\Omega_0}{\sqrt{2}}\,\vec{\imath}_2 + \dfrac{\Omega_0}{\sqrt{2}}\,\vec{k}_2. | |||
</math> | |||
</center> | |||
El momento angular respecto al centro de masas es | |||
<center> | |||
<math> | |||
\vec{L}_G = \overset\leftrightarrow{I}_G\cdot\vec{\omega}_{21} | |||
</math> | |||
</center> | |||
El tensor de inercia es | |||
<center> | |||
<math> | |||
\overset\leftrightarrow{I}_G = | |||
I | |||
\left[ | |||
\begin{array}{ccc} | |||
1/2 & 0 & 0\\ | |||
0 & 1/2 & 0\\ | |||
0 & 0 & 1 | |||
\end{array} | |||
\right]_2 | |||
</math> | |||
</center> | |||
con <math>I=mR^2/2</math>. El momento de inercia buscado es | |||
<center> | |||
<math> | |||
\vec{L}_G | |||
=I | |||
\left[ | |||
\begin{array}{ccc} | |||
1/2 & 0 & 0\\ | |||
0 & 1/2 & 0\\ | |||
0 & 0 & 1 | |||
\end{array} | |||
\right]_2 | |||
\left[ | |||
\begin{array}{c} | |||
\Omega_0/\sqrt{2} \\ 0 \\ \Omega_0/\sqrt{2} | |||
\end{array} | |||
\right]_2 | |||
= | |||
\dfrac{I\Omega_0}{\sqrt{2}}\,\left(\dfrac{1}{2}\,\vec{\imath}_2 + \vec{k}_2\right). | |||
</math> | |||
</center> | |||
Volvemos a la base "0", teniendo en cuenta que | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\imath}_2 = \dfrac{1}{\sqrt{2}}\,\vec{\imath}_0 + \dfrac{1}{\sqrt{2}}\,\vec{k}_0\\ | |||
\vec{k}_2 = -\dfrac{1}{\sqrt{2}}\vec{\imath}_0 + \dfrac{1}{\sqrt{2}}\vec{k}_0 | |||
\end{array} | |||
</math> | |||
</center> | |||
con lo que obtenemos | |||
<center> | |||
<math> | |||
\vec{L}_G = -\dfrac{1}{8}mR^2\Omega_0\,(\vec{\imath}_0-3\vec{k}_0). | |||
</math> | |||
</center> | |||
Hay que señalar que, para resolver la pregunta, hemos escogido los ejes del sólido "2" de modo que en el instante en que el centro del disco esté en el punto <math>B</math>, el eje <math>X_2</math> esté en el plano <math>OX_0Z_0</math>. Siempre podemos hacer esto, gracias a la degeneración diametral del disco. | |||
Para calcular la energía cinética aplicamos el Teorema de Koening | |||
<center> | |||
<math> | |||
T = T_{tras} + T_{rot}. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
T_{tras} = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2. | |||
</math> | |||
</center> | |||
En el instante pedido | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,B}_{21} = \vec{v}^{\,B}_{20} + \vec{v}^{\,B}_{01} | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{B}_{20} = -v_0\,\vec{k}_2 | |||
</math> | |||
</center> | |||
y | |||
<center> | |||
<math> | |||
\vec{v}^{\,B}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OB} | |||
= | |||
\dfrac{L\Omega_0}{\sqrt{2}}\,\vec{\jmath}_0. | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | |||
<math> | |||
\vec{v}^{\,B}_{21} = \dfrac{v_0}{\sqrt{2}}\,\vec{\imath}_0 + \dfrac{L\Omega_0}{\sqrt{2}}\,\vec{\jmath}_0 - \dfrac{v_0}{\sqrt{2}}\,\vec{k}_0. | |||
</math> | |||
</center> | |||
y | |||
<center> | |||
<math> | |||
T_{tras} = \dfrac{1}{2}m\,\left(v_0^2 + \dfrac{L^2\Omega_0^2}{2}\right). | |||
</math> | |||
</center> | |||
Para la energía cinética de rotación tenemos | |||
<center> | |||
<math> | |||
T_{rot} = \dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} | |||
= | |||
\dfrac{3}{16}mR^2\Omega_0^2. | |||
</math> | |||
</center> | |||
La energía cinética total es | |||
<center> | |||
<math> | |||
T = \dfrac{1}{16}m\,\left(8v_0^2 + (4L^2+3R^2)\Omega_0^2\right). | |||
</math> | |||
</center> | |||
[[Categoría:Problemas de cinemática del sólido rígido]] | |||
[[Categoría:Problemas de cinética del sólido rígido]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión actual - 16:11 25 sep 2023
Enunciado
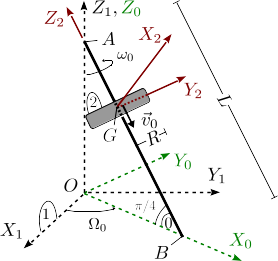
Un hilo rígido (sólido "0") de longitud rota alrededor del eje con velocidad angular constante , de modo que el punto está fijo y el punto describe una circunferencia sobre el plano . El hilo forma un ángulo con el plano . Un disco plano de masa y radio desliza por el hilo a la vez que rota alrededor de él con velocidad angular constante . En el instante inicial el centro del disco estaba en el punto . Se escoge un sólido "0" de modo que el plano contiene siempre al hilo. El sistema "2", solidario con el disco, se escoge de modo que el eje coincide con su eje de simetría y el eje es paralelo al eje . El punto del disco se mueve sobre el hilo con rapidez uniforme , como se indica en la figura.
- Calcula y .
- Calcula la velocidad absoluta del centro del disco en el instante inicial.
- ¿Qué condición tiene que cumplirse para que el movimiento {21} sea una rotación pura en el instante inicial?
- Supongamos que . En este caso, el momento cinético del disco respecto de su centro de masas y su energía cinética en el instante en el que el punto está en el punto .
Solución
Cálculo de y
Movimiento {01}
Tenemos
La derivada temporal es
Movimiento {20}
Tenemos
La derivada temporal es
No ponemos letra en la velocidad y aceleración pues es una traslación.
Movimiento {21}
Usando la composición {21}={20} + {01} tenemos
Expresamos el vector en la base "0"
Por tanto
También tenemos
Nótese que aunque {20} y {01} son dos rotaciones con aceleración angular nula, su composición tiene aceleración angular no nula.
Velocidad del centro del disco en el instante inicial
Usando la misma composición
En el instante inicial el punto está en el eje de giro del movimiento {01}, en el punto . Por tanto
El primer sumando es cero pues , y el segundo también pues y son paralelos. Entonces
Condición para que el movimiento {21} sea una rotación pura en el instante inicial
La condición que debe cumplirse es, que en ese instante, el invariante escalar del movimiento sea nulo, es decir
Cálculo del momento angular y la energía cinética
Con la condición tenemos
El momento angular respecto al centro de masas es
El tensor de inercia es
con . El momento de inercia buscado es
Volvemos a la base "0", teniendo en cuenta que
con lo que obtenemos
Hay que señalar que, para resolver la pregunta, hemos escogido los ejes del sólido "2" de modo que en el instante en que el centro del disco esté en el punto , el eje esté en el plano . Siempre podemos hacer esto, gracias a la degeneración diametral del disco.
Para calcular la energía cinética aplicamos el Teorema de Koening
Tenemos
En el instante pedido
Tenemos
y
Por tanto
y
Para la energía cinética de rotación tenemos
La energía cinética total es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 16:11 25 sep 2023 |  | 265 × 204 (13 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:





































![{\displaystyle {\overset {\leftrightarrow }{I}}_{G}=I\left[{\begin{array}{ccc}1/2&0&0\\0&1/2&0\\0&0&1\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f9ee61d7627421e1b73756208f91df8646a7b7)

![{\displaystyle {\vec {L}}_{G}=I\left[{\begin{array}{ccc}1/2&0&0\\0&1/2&0\\0&0&1\end{array}}\right]_{2}\left[{\begin{array}{c}\Omega _{0}/{\sqrt {2}}\\0\\\Omega _{0}/{\sqrt {2}}\end{array}}\right]_{2}={\dfrac {I\Omega _{0}}{\sqrt {2}}}\,\left({\dfrac {1}{2}}\,{\vec {\imath }}_{2}+{\vec {k}}_{2}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff998bcf23fb29a45d4632ae9c623e60118f24d)











