|
|
| Línea 1: |
Línea 1: |
| ==Enunciado== | | ==Enunciado== |
| Una partícula se mueve según las ecuaciones horarias | | Una partícula describe una curva cuya ecuación en coordenadas polares es |
|
| |
|
| <center><math>\vec{r}(t)=4A\cos(\Omega t)\vec{\imath}+ 5A\,\mathrm{sen}(\Omega t)\vec{\jmath}+3A\cos(\Omega t)\vec{k}</math></center> | | <center><math>\rho = A\cos(\Omega t)\qquad\qquad \theta = \Omega t</math></center> |
|
| |
|
| con A y Ω constantes.
| | # Calcule la velocidad y la aceleración en cada instante. |
| | # Halle las componentes intrínsecas de la aceleración para todo <math>t</math>. |
| | # Calcule el radio y el centro de curvatura en todo momento. |
| | # ¿De qué tipo de movimiento se trata? |
|
| |
|
| # ¿Qué trayectoria sigue la partícula?
| | ==Velocidad y aceleración== |
| # ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
| | ===Velocidad=== |
| # Justifique que este movimiento es circular y uniforme
| | La expresión de la velocidad empleando coordenadas polares es |
| # Determine la posición del centro del movimiento circular
| |
| # Calcule la velocidad angular de este movimiento circular
| |
|
| |
|
| ==Trayectoria== | | <center><math>\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\theta}\vec{u}_\theta</math></center> |
| Podemos identificar la trayectoria a partir de razonamientos puramente geométricos o empleando procedimientos cinemáticos.
| |
|
| |
|
| ===Identificación geométrica===
| | donde, en este caso |
| Si separamos las tres componentes del movimiento
| |
|
| |
|
| <center><math>\vec{r}:\left\{\begin{array}{rcl} x & = &4A\cos(\Omega t) \\ y & = & 5A\,\mathrm{sen}(\Omega t)\\ z & = & 3A\cos(\Omega t)\end{array}\right.</math></center> | | <center><math>\rho = A\cos(\Omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\Omega A\,\mathrm{sen}(\Omega t)\qquad\qquad\theta = \Omega t\qquad \dot{\theta}\equiv\frac{\mathrm{d}\theta}{\mathrm{d}t}=\Omega</math></center> |
|
| |
|
| De aquí es evidente que
| | que, sustituyendo nos da |
|
| |
|
| <center><math>z = \frac{3}{4}x\qquad\Rightarrow\qquad 3x-4z =0</math></center> | | <center><math>\vec{v}=\Omega A\left(-\mathrm{sen}(\Omega t)\vec{u}_\rho+\cos(\Omega t)\vec{u}_\theta\right)</math></center> |
|
| |
|
| Esta es la ecuación de un plano. También la podemos escribir en forma vectorial como
| | ===Aceleración=== |
| | La expresión correspondiente para la aceleración es |
|
| |
|
| <center><math>\vec{n}\cdot\vec{r}=0</math></center> | | <center><math>\vec{a}=\left(\ddot{\rho}-\rho\dot{\theta}^2\right)\vec{u}_\rho + \left(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta}\right)\vec{u}_\theta</math></center> |
|
| |
|
| ya que el vector de posición es
| | siendo |
|
| |
|
| <center><math>\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}</math></center> | | <center><math>\ddot{\rho}=-\Omega^2 A\cos(\Omega t)\qquad\qquad \ddot{\theta}=0</math></center> |
|
| |
|
| Si escribimos
| | lo que nos da la aceleración |
|
| |
|
| <center><math>\vec{n} = a\vec{\imath}+b\vec{\jmath}+c\vec{k}</math></center> | | <center><math>\vec{a}= -2\Omega^2 A\cos(\Omega t)\vec{u}_\rho-2\Omega^2 A\,\mathrm{sen}(\Omega t)\vec{u}_\theta</math></center> |
| | ==Componentes intrínsecas== |
| | ===Tangencial=== |
| | Una vez que tenemos la velocidad y la aceleración podemos hallar la aceleración tangencial algebraicamente |
|
| |
|
| El producto escalar es
| | <center><math>a_t = \frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}</math></center> |
|
| |
|
| <center><math>\vec{n}\cdot\vec{r} = ax + by +cz = 0</math></center>
| | o bien a partir de la rapidez |
|
| |
|
| Igualando coeficiente a coeficiente
| | <center><math>a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}</math></center> |
|
| |
|
| <center><math>a = 3,\qquad b = 0,\qquad c = -4</math></center>
| | Para emplear el segundo método, calculamos en primer lugar la rapidez |
|
| |
|
| así que un vector normal al plano es
| | <center><math>|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{(-\Omega A\,\mathrm{sen}(\Omega t))^2+(\Omega A\cos(\Omega t))^2}=\Omega A</math></center> |
|
| |
|
| <center><math>\vec{n}=3\vec{\imath}-4\vec{k}</math></center>
| | El movimiento es entonces uniforme y por tanto |
|
| |
|
| que es un vector constante. Si queremos un unitario perpendicular al plano
| | <center><math>a_t = \frac{\mathrm{d}\ }{\mathrm{d}t}(\Omega A) = 0</math></center> |
|
| |
|
| <center><math>|\vec{n}|=\sqrt{3^2+4^2} = 5</math></center>
| | Algebraicamente puede verse que la velocidad y la aceleración son ortogonales en todo momento, y por tanto se anula la componente tangencial. |
|
| |
|
| y queda
| | ===Normal=== |
| | Si la aceleración tangencial es nula, la aceleración normal es toda la que hay |
|
| |
|
| <center><math> \vec{B}=\frac{\vec{n}}{|\vec{n}|}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{k}</math></center> | | <center><math>\vec{a}_n = \vec{a}-\overbrace{\vec{a}_t}^{=\vec{0}} = -2\Omega^2 A\cos(\Omega t)\vec{u}_\rho-2\Omega^2 A\,\mathrm{sen}(\Omega t)\vec{u}_\theta</math></center> |
|
| |
|
| El vector <math>\vec{B}</math> es un vector constante ortogonal al plano de movimiento.
| | En módulo la aceleración normal vale |
|
| |
|
| Además tenemos que se cumple
| | <center><math>a_n = \sqrt{\vec{a}_n\cdot\vec{a}_n}= \sqrt{(2\Omega^2 A\cos(\Omega t))^2+(-2\Omega^2 A\,\mathrm{sen}(\Omega t))^2} = 2\Omega^2A</math></center> |
|
| |
|
| <center><math>x^2 + z^2 = 25A^2\cos^2(\Omega t)\qquad\qquad y^2 = 25A^2\mathrm{sen}^2(\Omega t)</math></center>
| | ==Radio y centro de curvatura== |
| | ===Radio de curvatura=== |
| | Conocidas la aceleración normal y la rapidez, hallamos el radio de curvatura. |
|
| |
|
| y sumando estas dos
| | <center><math>R = \frac{|\vec{v}|^2}{a_n} = \frac{\Omega^2A^2}{2\Omega^2 A}=\frac{A}{2}</math></center> |
|
| |
|
| <center><math>x^2 + y^2 + z^2 = 25A^2\,</math></center>
| | Vemos que resulta un radio de curvatura constante. |
|
| |
|
| que es la ecuación de una esfera de radio <math>R=5A</math>.
| | ===Centro de curvatura=== |
| | | El centro de curvatura lo obtenemos a partir del vector de posición, el vector normal y el radio de curvatura |
| la trayectoria es entonces la intersección de un plano y una esfera. Esa intersección es siempre una circunferencia. Por tanto el movimiento es circular.
| |
| | |
| <center>[[Archivo:corte-plano-esfea.png]]</center>
| |
| | |
| ===Procedimiento cinemático=== | |
| El método anterior es muy simple para determinar que el movimiento es plano, pero no siempre se encuentra a la primera qué combinación lineal de las variables nos da la ecuación del plano, si este existe.
| |
| | |
| Por ello, existen procedimiento sistemáticos para determinar esta situación.
| |
| | |
| Uno es el siguiente: hay que hallar la velocidad, la aceleración y la derivada de ésta respecto al tiempo. El movimiento es plano si y solo si se cumple la condición
| |
| | |
| <center><math>(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=0</math></center>
| |
| | |
| En nuestro caso tenemos
| |
| | |
| <center><math>\begin{array}{ccccccc}
| |
| \vec{v}(t) & = & -4A\Omega\,\mathrm{sen}(\Omega t)\vec{\imath}& + & 5A\Omega\,\mathrm{cos}(\Omega t)\vec{\jmath}& - & 3A\Omega\,\mathrm{sen}(\Omega t)\vec{k}\\
| |
| \vec{a}(t)& = & -4A\Omega^2\,\mathrm{cos}(\Omega t)\vec{\imath}& - & 5A\Omega^2\,\mathrm{sen}(\Omega t)\vec{\jmath}& - & 3A\Omega^2\,\mathrm{cos}(\Omega t)\vec{k}\\
| |
| \dot{\vec{a}}(t) & = & +4A\Omega^3\,\mathrm{sen}(\Omega t)\vec{\imath}& - &5A\Omega^3\,\mathrm{cos}(\Omega t)\vec{\jmath}& + & 3A\Omega^3\,\mathrm{sen}(\Omega t)\vec{k}\end{array}
| |
| </math></center>
| |
| | |
| El producto vectorial de la velocidad y la aceleración lo da el el determinante | |
| | |
| <center><math>\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -4A\Omega\,\mathrm{sen}(\Omega t) & 5A\Omega\,\mathrm{cos}(\Omega t)& - 3A\Omega\,\mathrm{sen}(\Omega t)\\
| |
| -4A\Omega^2\,\mathrm{cos}(\Omega t)& -5A\Omega^2\,\mathrm{sen}(\Omega t)& -3A\Omega^2\,\mathrm{cos}(\Omega t)\end{matrix}\right|=-15A^2\Omega^3\vec{\imath}+20A^2\Omega^3\vec{k}</math></center>
| |
| | |
| Siendo el producto mixto de los tres vectores
| |
| | |
| <center><math>(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=
| |
| -15A^2\Omega^3\left(4A\Omega^3\,\mathrm{sen}(\Omega t)\right)+20A^2\Omega^3\left(3A\Omega^3\,\mathrm{sen}(\Omega t)\right)=0</math></center>
| |
| | |
| Con eso ya tenemos que la trayectoria es plana. Para ver que además es circular vamos a calcular el radio de curvatura, según la fórmula
| |
| | |
| <center><math>R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}</math></center>
| |
| | |
| La rapidez del movimiento vale
| |
| | |
| <center><math>|\vec{v}|=\sqrt{16A^2\Omega^2\mathrm{sen}^2(\Omega t)+25A^2\Omega^2\mathrm{cos}^2(\Omega t)+9A^2\Omega^2\mathrm{sen}^2(\Omega t)}=5A\Omega</math></center>
| |
| | |
| Esta cantidad es constante por lo que ya sabemos además que el movimiento es uniforme.
| |
| | |
| Hallamos ahora el radio de curvatura
| |
| | |
| <center><math>R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}=\frac{(5A\Omega)^3}{A^2\Omega^3\sqrt{15^2+20^2}}=5A</math></center>
| |
| | |
| El radio de curvatura es constante.
| |
| | |
| Si el movimiento es plano y el radio de curvatura es constante, se trata de un movimiento circular.
| |
| | |
| ==Desplazamiento y distancia==
| |
| ===Desplazamiento===
| |
| Lo da la diferencia entre la posición final y la inicial
| |
| | |
| <center><math>\Delta\vec{r}=\vec{r}_f-\vec{r}_i</math></center>
| |
| | |
| Siendo la posición inicial
| |
| | |
| <center><math>\vec{r}_i=\vec{r}(t=0)=4A\cdot 1\vec{\imath}+5A\cdot0\vec{\jmath}+3A\cdot 1\vec{k}=4A\vec{\imath}+3A\vec{k}</math></center>
| |
| | |
| y la final la correspondiente a <math>\Omega t = \pi</math>
| |
| | |
| <center><math>\vec{r}_f=\vec{r}(t=\pi/\Omega)=4A\cdot(- 1)\vec{\imath}+5A\cdot0\vec{\jmath}+3A\cdot(- 1)\vec{k}=-4A\vec{\imath}-3A\vec{k}</math></center>
| |
| | |
| El desplazamiento vale entonces
| |
| | |
| <center><math>\Delta \vec{r}=-8A\vec{\imath}-6A\vec{k}</math></center>
| |
| | |
| El valor absoluto de este desplzamiento es la distancia en línea recta entre los dos puntos
| |
| | |
| <center><math>|\Delta\vec{r}| = \sqrt{64A^2+36A^2}=10A</math></center>
| |
| | |
| ===Distancia===
| |
| La calculamos integrando la rapidez
| |
| | |
| <center><math>\Delta s = \int_0^{\pi/\Omega} |\vec{v}|\mathrm{d}t = \int_0^{\pi/\Omega} 5A\Omega\,\mathrm{d}t = 5\pi A</math></center>
| |
| | |
| Esta distancia medida sobre la curva es mayor que la que se tiene en línea recta, que es la menor posible.
| |
| | |
| La interpretación es sencilla. Este movimiento es periódico. Cuando el argumento <math>\Omega t</math> varía en <math>2\pi</math> el seno y el coseno se repiten y la partícula vuelve a estar en la posición inicial. El tiempo que tarda en dar una vuelta completa es el periodo de revolución
| |
| | |
| <center><math>T=\frac{2\pi}{\Omega}</math></center>
| |
| | |
| Por tanto, el intervalo que estamos considerando es media vuelta. La distancia en línea recta es el diámetro de la circunferencia
| |
| | |
| <center><math>|\Delta\vec{r}| = 2R = 10A</math></center>
| |
| | |
| y la distancia sobre la curva es la longitud de media circunferencia | |
| | |
| <center><math>\Delta s = \pi R = 5\pi A\,</math></center>
| |
| | |
| ==Tipo de movimiento==
| |
| En los apartados anteriores ya hemos establecido todo lo necesario para identificar el movimiento:
| |
| | |
| * Es plano
| |
| * Tiene radio de curvatura constante
| |
| * Tiene rapidez constante
| |
| | |
| Por tanto se trata de un movimiento circular uniforme.
| |
| | |
| ==Centro de la circunferencia==
| |
| El centro de la circunferencia coincide con el centro de curvatura
| |
|
| |
|
| <center><math>\vec{r}_c = \vec{r}+R\vec{N}</math></center> | | <center><math>\vec{r}_c = \vec{r}+R\vec{N}</math></center> |
|
| |
|
| En este caso, al ser el movimiento uniforme la aceleración tangencial es nula y toda la aceleración es normal, por lo que
| | El vector normal en este caso es el unitario en la dirección y sentido de la aceleración normal |
| | |
| <center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=\frac{\vec{a}}{|\vec{a}|}=
| |
| \frac{ -4A\Omega^2\,\mathrm{cos}(\Omega t)\vec{\imath} - 5A\Omega^2\,\mathrm{sen}(\Omega t)\vec{\jmath} - 3A\Omega^2\,\mathrm{cos}(\Omega t)\vec{k}}{5A\Omega^2}=</math><math>=-\frac{4}{5}\,\mathrm{cos}(\Omega t)\vec{\imath} - \mathrm{sen}(\Omega t)\vec{\jmath} - \frac{3}{5}\,\mathrm{cos}(\Omega t)\vec{k}</math></center>
| |
| | |
| El radio de la circunferencia vale 5A, por lo que el centro se halla en
| |
| | |
| <center><math>\vec{r}_c = \left(4A\,\mathrm{cos}(\Omega t)\vec{\imath} +55A\,\mathrm{sen}(\Omega t)\vec{\jmath} +3A\,\mathrm{cos}(\Omega t)\vec{k}\right)+5A\left(-\frac{4}{5}\,\mathrm{cos}(\Omega t)\vec{\imath} - \mathrm{sen}(\Omega t)\vec{\jmath} - \frac{3}{5}\,\mathrm{cos}(\Omega t)\vec{k}\right)=\vec{0}</math></center>
| |
| | |
| Es decir, el centro de la circunferencia es el propio origen de coordenadas.
| |
| | |
| Esto se podía haber deducido de una forma más sencilla observando que cada coordenada es un seno o un coseno, por lo que la trayectoria es simétrica alrededor de <math>x=y=z=0</math> que es por tanto el centro de la circunferencia.
| |
| | |
| ==Cálculo de la velocidad angular==
| |
| Una vez que tenemos identificado el movimiento como circular podemos identificar la velocidad angular a partir de la ecuación
| |
| | |
| <center><math>\vec{v}=\vec{\omega}\times(\vec{r}-\vec{r}_c)</math></center>
| |
| | |
| La velocidad angular es un vector que tiene por dirección la del eje de la circunferencia, por sentido el dado por la regla de la mano derecha y por módulo el que resulta de
| |
| | |
| <center><math>|\vec{\omega}|=\frac{|\vec{v}|}{R}</math></center>
| |
|
| |
|
| Existen varias formas de determinar este vector
| | <center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|} = -\cos(\Omega t)\vec{u}_\rho-\,\mathrm{sen}(\Omega t)\vec{u}_\theta</math></center> |
|
| |
|
| ===A partir del módulo, dirección y sentido===
| | mientras que el vector de posición viene dado por |
| El módulo de esta velocidad angular cumple
| |
|
| |
|
| <center><math>|\vec{\omega}|=\frac{|\vec{v}|}{R}=\frac{5\Omega A}{5A}=\Omega</math></center> | | <center><math>\vec{r} = \rho\vec{u}_\rho = A\cos(\Omega t)\vec{u}_\rho</math></center> |
|
| |
|
| La dirección es la del eje. Este eje está en la dirección de la normal al plano de la circunferencia, dada por el vector unitario
| | lo que nos da el centro de curvatura |
|
| |
|
| <center><math>\vec{B}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{k}</math></center> | | <center><math>\vec{r}_c = \left(A\cos(\Omega t)\vec{u}_\rho \right)+\frac{A}{2}\left( -\cos(\Omega t)\vec{u}_\rho-\,\mathrm{sen}(\Omega t)\vec{u}_\theta\right)=\frac{A}{2}\cos(\Omega t)\vec{u}_\rho-\frac{A}{2}\,\mathrm{sen}(\Omega t)\vec{u}_\theta</math></center> |
|
| |
|
| Por tanto
| | ==Identificación del movimiento== |
| | Hemos obtenido que: |
|
| |
|
| <center><math>\vec{\omega}=\pm |\vec{\omega}|\vec{B}=\pm\left(\frac{3}{5}\Omega\vec{\imath}-\frac{4}{5}\Omega\vec{k}\right)</math></center>
| | * El movimiento es plano |
| | * El radio de curvatura es constante |
| | * La rapidez es constante |
|
| |
|
| La dualidad de signos no se debe a que tenga los dos valores al mismo tiempo, sino a que aun no tenemos claro el sentido de este vector, ya que la regla de la mano derecha no es inmediata de ver en 3D. | | Estas tres propiedades identifican el movimiento como '''circular uniforme'''. La partícula describe circunferencias a ritmo constante alrededor de un punto fijo que es el centro de curvatura. |
|
| |
|
| La forma más fácil de determinar el sentido es yendo directamente a la ecuación
| | A la vista de la expresión del centro de curvatura |
|
| |
|
| <center><math>\vec{v}=\vec{\omega}\times\vec{r}</math></center> | | <center><math>\vec{r}_c = \frac{A}{2}\cos(\Omega t)\vec{u}_\rho-\frac{A}{2}\,\mathrm{sen}(\Omega t)\vec{u}_\theta</math></center> |
|
| |
|
| donde ya hemos aplicado que sabemos que la partícula da vueltas alrededor del origen.
| | parecería que este punto es variable en el tiempo. Sin embargo, no es así. Si en lugar de la base vectorial de polares empleamos la de cartesianas, relacionada con la otra por |
|
| |
|
| Desarrollando la expresión queda
| | <center><math>\begin{array}{rcl} |
| | \vec{\imath} & = & \cos(\theta)\vec{u}_\rho-\mathrm{sen}(\theta)\vec{u}_\theta \\ |
| | \vec{\jmath} & = & \mathrm{sen}(\theta)\vec{u}_\rho+\cos(\theta)\vec{u}_\theta |
| | \end{array}</math></center> |
|
| |
|
| <center><math> -4A\Omega\,\mathrm{sen}(\Omega t)\vec{\imath} + 5A\Omega\,\mathrm{cos}(\Omega t)\vec{\jmath} - 3A\Omega\,\mathrm{sen}(\Omega t)\vec{k}=\pm \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \displaystyle\frac{3}{5}\Omega & 0 & \displaystyle -\frac{4}{5}\Omega \\ 4A\Omega\,\mathrm{cos}(\Omega t) & 5A\Omega\,\mathrm{sen}(\Omega t) & 3A\Omega\,\mathrm{cos}(\Omega t)\end{matrix}\right|</math></center>
| | vemos que |
|
| |
|
| Desarrollando el determinante e igualando a la velocidad que aparece en el primer miembro se llega a que el signo correcto es el negativo y por tanto:
| | <center><math>\vec{r}_c = \frac{A}{2}\vec{\imath}</math></center> |
|
| |
|
| <center><math>\vec{\omega}=-\frac{3}{5}\Omega\vec{\imath}+\frac{4}{5}\Omega\vec{k}</math></center>
| | que es evidentemente un punto fijo. |
|
| |
|
| ===Despejando de la velocidad===
| | Conocido el radio y la rapidez, obtenemos la velocidad angular dividiendo una por el otro |
| Lo que parecería más sencillo sería despejar de la expresión
| |
|
| |
|
| <center><math>\vec{\omega}\times\vec{r}=\vec{v}</math></center> | | <center><math>\omega = \frac{|\vec{v}|}{R}=\frac{\Omega A}{A/2} = 2\Omega</math></center> |
|
| |
|
| Pero como sabemos, solo con el producto vectorial no tenemos información suficiente para hallar un vector y desde luego no podemos dividir por uno.
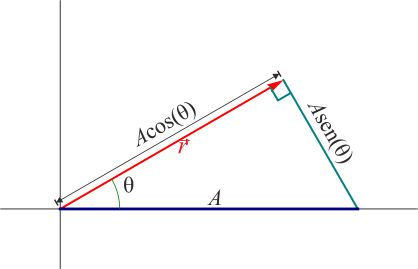
| | Podemos describir la trayectoria sin recurrir a su expresión en cartesianas, observando que en cada instante el vector de posición forma un ángulo <math>\theta=\Omega t</math> con el eje OX y tiene por módulo <math>A\cos(\theta)</math>. Esto quiere decir que se puede considerar un cateto de un triángulo rectángulo de ángulo <math>\theta</math>. La hipotenusa de este triángulo mide <math>A</math> para todo instante y se encuentra sobre el eje OX. |
|
| |
|
| Tal como se ve en un problema de [[Determinaci%C3%B3n_de_un_vector_a_partir_de_sus_proyecciones|álgebra vectorial]], para poder hallar un vector <math>\vec{\omega}</math> necesitamos tanto su producto vectorial por uno conocido <math>\vec{r}</math> como su producto escalar.
| | <center>[[Archivo:circunferencia-excentrica-01.png|418px]]</center> |
|
| |
|
| Sin embargo, en este caso, sí conocemos este producto escalar. El vector de posición <math>\vec{r}</math> está en el plano de la circunferencia y <math>\vec{\omega}</math> es perpendicular a este plano, por lo que
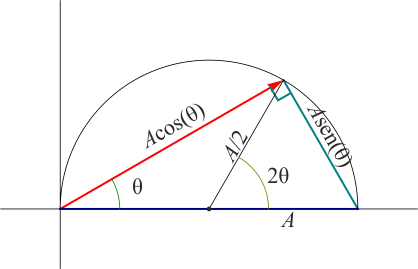
| | Ahora bien, según se ve en el estudio del [[Arco capaz (GIE)|arco capaz]] si tenemos un triángulo cuya hipotenusa AB es fija y cuyo ángulo en el vértice va variando, el tercer vértice P describe un arco de circunferencia de radio <math>A/2</math>. El ángulo que forma CP con el eje OX es el doble del del vértice, <math>\theta = 2\theta =2\Omega t</math>. |
|
| |
|
| <center><math>\vec{\omega}\cdot\vec{r}=\vec{0}</math></center> | | <center>[[Archivo:circunferencia-excentrica-02.png|418px]]</center> |
|
| |
|
| Por tanto sí tenemos los dos productos y podemos hallar la velocidad angular.
| | Vemos entonces que la partícula efectivamente describe una circunferencia con velocidad angular constante, siendo su velocidad angular <math>\vec{\omega}=2\Omega\vec{k}</math> |
|
| |
|
| En la ecuación para la velocidad lineal multiplicamos vectorialmente por la posición
| | <center>[[Archivo:circunferencia-excentrica-02.gif]]</center> |
|
| |
|
| <center><math>\vec{r}\times(\vec{\omega}\times\vec{r})=\vec{r}\times\vec{v}</math></center>
| | Esta identificación también se puede hacer empleando coordenadas cartesianas. La ecuación de la trayectoria, en polares, es |
|
| |
|
| Desarrollamos el doble producto vectorial
| | <center><math>\rho = A\cos(\theta)\,</math></center> |
|
| |
|
| <center><math>\overbrace{(\vec{r}\cdot\vec{r})}^{=R^2}\vec{\omega}-\overbrace{(\vec{r}\cdot\vec{\omega})}^{=0}\vec{r}=R^2\vec{\omega}=\vec{r}\times\vec{v}</math></center>
| | Si multiplicamos por <math>\rho</math> en los dos miembros nos queda |
|
| |
|
| y por tanto
| | <center><math>\rho^2 = A\rho \cos(\theta)\,</math></center> |
|
| |
|
| <center><math>\vec{\omega}=\frac{\vec{r}\times\vec{v}}{R^2}</math></center>
| | y esto, en cartesianas, se escribe |
|
| |
|
| Sustituimos aquí las expresiones del radio, la posición y la velocidad
| | <center><math>x^2 +y^2 = A x \,</math></center> |
|
| |
|
| <center><math>\vec{\omega}=\frac{1}{25A^2} \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4A\Omega\,\mathrm{cos}(\Omega t) & 5A\Omega\,\mathrm{sen}(\Omega t) & 3A\Omega\,\mathrm{cos}(\Omega t) \\ -4A\Omega\,\mathrm{sen}(\Omega t) & 5A\Omega\,\mathrm{cos}(\Omega t) & - 3A\Omega\,\mathrm{sen}(\Omega t)\end{matrix}\right|</math></center>
| | o, equivalentemente, |
|
| |
|
| Desarrollando el determinante se llega finalmente a que
| | <center><math>\left(x-\frac{A}{2}\right)^2 + y^2 = \left(\frac{A}{2}\right)^2</math></center> |
|
| |
|
| <center><math>\vec{\omega}=-\frac{3}{5}\Omega\vec{\imath}+\frac{4}{5}\Omega\vec{k}</math></center>
| | que es la ecuación de una circunferencia de centro <math>\vec{r}_c = (A/2)\vec{\imath}</math> y radio <math>A/2</math>. |
|
| |
|
| [[Categoría:Problemas de cinemática tridimensional de la partícula (GIOI)]] | | [[Categoría:Problemas de cinemática de la partícula (GIOI)]] |
| | [[Categoría:Problemas de cinemática tridimensional (GIOI)]] |
Enunciado
Una partícula describe una curva cuya ecuación en coordenadas polares es

- Calcule la velocidad y la aceleración en cada instante.
- Halle las componentes intrínsecas de la aceleración para todo
 .
.
- Calcule el radio y el centro de curvatura en todo momento.
- ¿De qué tipo de movimiento se trata?
Velocidad y aceleración
Velocidad
La expresión de la velocidad empleando coordenadas polares es

donde, en este caso

que, sustituyendo nos da

Aceleración
La expresión correspondiente para la aceleración es

siendo

lo que nos da la aceleración

Componentes intrínsecas
Tangencial
Una vez que tenemos la velocidad y la aceleración podemos hallar la aceleración tangencial algebraicamente

o bien a partir de la rapidez

Para emplear el segundo método, calculamos en primer lugar la rapidez

El movimiento es entonces uniforme y por tanto

Algebraicamente puede verse que la velocidad y la aceleración son ortogonales en todo momento, y por tanto se anula la componente tangencial.
Normal
Si la aceleración tangencial es nula, la aceleración normal es toda la que hay

En módulo la aceleración normal vale

Radio y centro de curvatura
Radio de curvatura
Conocidas la aceleración normal y la rapidez, hallamos el radio de curvatura.

Vemos que resulta un radio de curvatura constante.
Centro de curvatura
El centro de curvatura lo obtenemos a partir del vector de posición, el vector normal y el radio de curvatura

El vector normal en este caso es el unitario en la dirección y sentido de la aceleración normal

mientras que el vector de posición viene dado por

lo que nos da el centro de curvatura

Identificación del movimiento
Hemos obtenido que:
- El movimiento es plano
- El radio de curvatura es constante
- La rapidez es constante
Estas tres propiedades identifican el movimiento como circular uniforme. La partícula describe circunferencias a ritmo constante alrededor de un punto fijo que es el centro de curvatura.
A la vista de la expresión del centro de curvatura

parecería que este punto es variable en el tiempo. Sin embargo, no es así. Si en lugar de la base vectorial de polares empleamos la de cartesianas, relacionada con la otra por

vemos que

que es evidentemente un punto fijo.
Conocido el radio y la rapidez, obtenemos la velocidad angular dividiendo una por el otro

Podemos describir la trayectoria sin recurrir a su expresión en cartesianas, observando que en cada instante el vector de posición forma un ángulo  con el eje OX y tiene por módulo
con el eje OX y tiene por módulo  . Esto quiere decir que se puede considerar un cateto de un triángulo rectángulo de ángulo
. Esto quiere decir que se puede considerar un cateto de un triángulo rectángulo de ángulo  . La hipotenusa de este triángulo mide
. La hipotenusa de este triángulo mide  para todo instante y se encuentra sobre el eje OX.
para todo instante y se encuentra sobre el eje OX.
Ahora bien, según se ve en el estudio del arco capaz si tenemos un triángulo cuya hipotenusa AB es fija y cuyo ángulo en el vértice va variando, el tercer vértice P describe un arco de circunferencia de radio  . El ángulo que forma CP con el eje OX es el doble del del vértice,
. El ángulo que forma CP con el eje OX es el doble del del vértice,  .
.
Vemos entonces que la partícula efectivamente describe una circunferencia con velocidad angular constante, siendo su velocidad angular 
Archivo:Circunferencia-excentrica-02.gif
Esta identificación también se puede hacer empleando coordenadas cartesianas. La ecuación de la trayectoria, en polares, es

Si multiplicamos por  en los dos miembros nos queda
en los dos miembros nos queda

y esto, en cartesianas, se escribe

o, equivalentemente,

que es la ecuación de una circunferencia de centro  y radio
y radio  .
.





































