No Boletín - Camino más corto entre un punto y una recta (Ex.Oct/14)

Enunciado

En un sistema cartesiano $OXYZ\,$ se define el punto $P\,$ (de posición ${\overrightarrow {OP}}={\vec {\imath }}+{\vec {k}}\,$) y la recta $r\,$ (que pasa por el punto $Q\,$ de posición ${\overrightarrow {OQ}}=3\,{\vec {\imath }}+5\,{\vec {k}}\,$, y es paralela al vector ${\vec {w}}=3\,{\vec {\imath }}-{\vec {\jmath }}+2\,{\vec {k}}\,$). Determine el vector que coincide con el camino más corto que lleva desde el punto $P\,$ hasta la recta $r\,$.

Solución

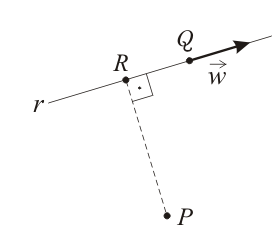
El camino más corto que lleva desde el punto $P\,$ hasta la recta $r\,$ coincide con un vector ortogonal a $r\,$ que tiene su origen en $P\,$ y su extremo en un punto de $r\,$ (punto al que llamaremos $R\,$). Por tanto, nuestro objetivo en este ejercicio consiste en calcular dicho vector ${\overrightarrow {PR}}\,$.

Sabemos que la recta $r\,$ pasa por el punto $Q(3,0,5)\,$ y admite como vector director a ${\vec {w}}=3\,{\vec {\imath }}-{\vec {\jmath }}+2\,{\vec {k}}\,$. Por tanto, las coordenadas de un punto genérico de dicha recta (ecuaciones $\lambda$-paramétricas de $r\,$) son:

$\left\{{\begin{array}{l}x=3+3\,\lambda \\y=-\,\lambda \\z=5+2\,\lambda \end{array}}\right.$

Si a las coordenadas de este punto genérico de $r\,$ les restamos las coordenadas del punto $P(1,0,1)\,$, deducimos que el vector que va desde $P\,$ hasta un punto genérico de $r\,$ vale $(\,2+3\,\lambda )\,{\vec {\imath }}-\,\lambda \,{\vec {\jmath }}+(\,4+2\,\lambda \,)\,{\vec {k}}\,$.

Finalmente, determinamos el vector ${\overrightarrow {PR}}\,$ exigiendo su ortogonalidad a $r\,$ y, por tanto, al vector ${\vec {w}}\,$: ${\overrightarrow {PR}}\perp {\vec {w}}\,\,\,\rightarrow \,\,\,{\overrightarrow {PR}}\,\cdot \,{\vec {w}}=\left[\,(\,2+3\,\lambda )\,{\vec {\imath }}-\,\lambda \,{\vec {\jmath }}+(\,4+2\,\lambda \,)\,{\vec {k}}\,\right]\,\cdot \left(\,3\,{\vec {\imath }}-{\vec {\jmath }}+2\,{\vec {k}}\,\right)=14\,\lambda \,+\,14=0\,\,\,\rightarrow$ $\rightarrow \,\,\,\lambda =-\,1\,\,\,\rightarrow \,\,\,{\overrightarrow {PR}}=-\,{\vec {\imath }}\,\,+\,{\vec {\jmath }}\,\,+\,2\,{\vec {k}}$

Procedimiento alternativo

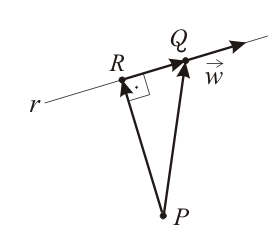
Un procedimiento alternativo consiste en descomponer el vector ${\overrightarrow {PQ}}\,$ como la suma de dos vectores: uno perpendicular a ${\vec {w}}\,$ y otro paralelo a ${\vec {w}}\,$ (en la teoría se ha deducido una fórmula para este tipo de descomposición), y a continuación darse cuenta de que el vector ${\overrightarrow {PR}}\,$ buscado coincide precisamente con el vector perpendicular a ${\vec {w}}\,$ de la citada descomposición:

${\overrightarrow {PQ}}=\underbrace {\frac {({\vec {w}}\times {\overrightarrow {PQ}})\times {\vec {w}}}{|\,{\vec {w}}\,|^{2}}} _{\overrightarrow {PR}}\,+\,\underbrace {\frac {({\vec {w}}\cdot {\overrightarrow {PQ}})\,{\vec {w}}}{|\,{\vec {w}}\,|^{2}}} _{\overrightarrow {RQ}}$

Así que, restando las coordenadas de $P\,$ a las coordenadas de $Q\,$, determinamos el vector ${\overrightarrow {PQ}}=2\,{\vec {\imath }}+4\,{\vec {k}}\,$; y, aplicando la fórmula correspondiente, obtenemos:

${\overrightarrow {PR}}={\frac {({\vec {w}}\times {\overrightarrow {PQ}})\times {\vec {w}}}{|\,{\vec {w}}\,|^{2}}}=-\,{\vec {\imath }}\,\,+\,{\vec {\jmath }}\,\,+\,2\,{\vec {k}}$