Diferencia entre las páginas «Barra con traslación y rotación (Nov. 2018 G.I.C.)» y «Masa colgando de cuerda y muelle (Nov. 2018 G.I.C.)»
(Página creada con «= Enunciado = right|250px Una barra de longitud <math>L</math> se mueve de modo que su extremo <math>A</math> se desplaza sobre el eje <math>OY</math> con velocidad uniforme <math>v_0</math> y el ángulo que forma la barra con el eje <math>OX</math> es <math>\theta=\omega_0 t</math>. En el instante inicial el punto <math>A</math> estaba en el origen y la barra estaba horizontal, es decir <math>\theta(0)=0</math>. # Escri…») |
(Página creada con «= Enunciado = right|250px Una partícula de masa <math>m</math> cuelga de una cuerda de longitud <math>L</math> y un muelle de constante elástica <math>k</math> y longitud natural nula, como se indica en la figura. El punto <math>B</math> de anclaje del muelle está a una distancia <math>L</math> del origen. Supondremos que la cuerda está tensa en todo momento. #Dibuja el diagrama de fuerzas que actúan sobre la mas…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | = Enunciado = | ||
[[Archivo: | [[Archivo:F!GIC-masa-cuerda-muelle-enunicado.png|right|250px]] | ||
Una | Una partícula de masa <math>m</math> cuelga de una cuerda de longitud <math>L</math> y un muelle de constante elástica <math>k</math> y longitud natural nula, como se indica en la figura. El punto <math>B</math> de anclaje del muelle está a una distancia <math>L</math> del origen. Supondremos que la cuerda está tensa en todo momento. | ||
#Dibuja el diagrama de fuerzas que actúan sobre la masa <math>m</math> y el punto <math>A</math>. Muestra correctamente la dirección y sentido de todas las fuerzas. | |||
# Escribe la expresión del vector <math>\overrightarrow{BA}</math> | |||
# | #Suponiendo que <math>mg = kL</math>, ¿cuál es el valor de <math>\alpha</math> para el que hay equilibrio mecánico? | ||
# | #Para la situación de la pregunta anterior, ¿cuánto vale la tensión en la cuerda que une los puntos <math>O</math> y <math>A</math>? | ||
# | |||
= Solución = | = Solución = | ||
== Diagrama de fuerzas == | |||
[[Archivo:F1GIC-masa-cuerda-muelle-fuerzas.png|right]] | |||
La figura muestra las fuerzas que actúan sobre la masa y el punto <math>A</math>. La fuerzas sobre la masa son su peso y la fuerza del trozo de cuerda entre ella y el punto <math>A</math>. Sobre el punto <math>A</math> actúan la fuerza que ejerce el trozo de cuerda debajo de él, la que ejerce el trozo entre <math>O</math> y <math>A</math> y la del muelle. | |||
== Expresión del vector <math>\overrightarrow{BA}</math> == | |||
Este vector puede escribirse como | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{ | \overrightarrow{BA} = \overrightarrow{OA} - \overrightarrow{OB}. | ||
</math> | </math> | ||
</center> | </center> | ||
Estos dos vectores son | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{OA} = | \begin{array}{l} | ||
\overrightarrow{OA} = L\cos\alpha\,\vec{\imath} + L\,\mathrm{sen}\,\alpha\,\vec{\jmath}, \\ | |||
\overrightarrow{OB} = L\,\vec{\jmath}. | |||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
Entonces | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{ | \overrightarrow{BA} = L\cos\alpha\,\vec{\imath} + L\,(\,\mathrm{sen}\,\alpha - 1)\,\vec{\jmath}. | ||
</math> | </math> | ||
</center> | </center> | ||
== | == Posición de equilibrio == | ||
Escribimos las fuerzas del diagrama en el sistema de ejes de la figura. Sobre la masa <math>m</math> tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \begin{array}{l} | ||
\vec{P}_m = mg\,\vec{\imath},\\ | |||
= | \vec{T}_m = -T_m\,\vec{\imath}. | ||
- | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
Sobre el punto <math>A</math> tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \begin{array}{l} | ||
\vec{T}_A = - \vec{T}_m = T_m\,\vec{\imath},\\ | |||
= | \vec{T}_O = -T_O\cos\alpha\,\vec{\imath} - T_O\,\mathrm{sen}\,\alpha\,\vec{\jmath},\\ | ||
- | \vec{F}_k = -k\overrightarrow{BA} = -kL\cos\alpha\,\vec{\imath} - kL\,(\,\mathrm{sen}\,\alpha -1 )\,\vec{\jmath}. | ||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
Aplicamos la condición de equilibrio a cada cuerpo. Para la masa | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \vec{P}_m + \vec{T}_m = \vec{0} | ||
\Longrightarrow | |||
T_m = mg. \qquad\qquad (1) | |||
</math> | </math> | ||
</center> | </center> | ||
Para el punto <math>A</math> | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \vec{T}_A + \vec{T}_O + \vec{F}_k = \vec{0} | ||
\vec{ | \Longrightarrow | ||
\ | \left\{ | ||
\begin{array}{lclr} | |||
X) & \to & T_m - T_O\cos\alpha - kL\cos\alpha = 0, & (2)\\ | |||
Y) & \to & - T_O\,\mathrm{sen}\,\alpha - kL\,(\mathrm{sen}\,\alpha -1) = 0.& (3) | |||
\end{array} | \end{array} | ||
\right. | |||
</math> | </math> | ||
</center> | </center> | ||
Usando la condición dada por el enunciado, <math>mg=kL</math>, y la ecuación (1), las ecuaciones (2) y (3) quedan | |||
<center> | <center> | ||
<math> | <math> | ||
\begin{array}{ | \begin{array}{lcl} | ||
\ | (2) & \to &kL = (T_O+kL)\cos\alpha,\\ | ||
\ | (3) & \to &kL = (T_O+kL)\,\mathrm{sen}\,\alpha. | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
Dividiendo estas dos ecuaciones tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\tan\alpha = 1 | |||
\Longrightarrow | |||
\alpha = \pi/4. | |||
</math> | </math> | ||
</center> | </center> | ||
Ahora sustituimos en (3) para obtener la tensión de la cuerda <math>T_O</math> | |||
<center> | <center> | ||
<math> | <math> | ||
T_O = kL\,(\sqrt{2}-1). | |||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría: | [[Categoría:Dinámica del punto material|1]] | ||
[[Categoría:Problemas de dinámica de la partícula]] | |||
[[Categoría:Problemas de examen]] | [[Categoría:Problemas de examen]] | ||
[[Categoría:Problemas de examen de F1 GIC]] | [[Categoría:Problemas de examen de F1 GIC]] | ||
Revisión actual - 10:53 3 nov 2023
Enunciado
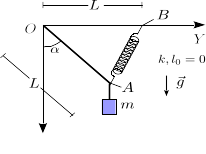
Una partícula de masa cuelga de una cuerda de longitud y un muelle de constante elástica y longitud natural nula, como se indica en la figura. El punto de anclaje del muelle está a una distancia del origen. Supondremos que la cuerda está tensa en todo momento.
- Dibuja el diagrama de fuerzas que actúan sobre la masa y el punto . Muestra correctamente la dirección y sentido de todas las fuerzas.
- Escribe la expresión del vector
- Suponiendo que , ¿cuál es el valor de para el que hay equilibrio mecánico?
- Para la situación de la pregunta anterior, ¿cuánto vale la tensión en la cuerda que une los puntos y ?
Solución
Diagrama de fuerzas
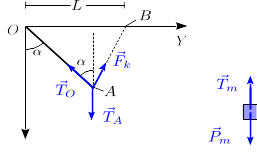
La figura muestra las fuerzas que actúan sobre la masa y el punto . La fuerzas sobre la masa son su peso y la fuerza del trozo de cuerda entre ella y el punto . Sobre el punto actúan la fuerza que ejerce el trozo de cuerda debajo de él, la que ejerce el trozo entre y y la del muelle.
Expresión del vector
Este vector puede escribirse como
Estos dos vectores son
Entonces
Posición de equilibrio
Escribimos las fuerzas del diagrama en el sistema de ejes de la figura. Sobre la masa tenemos
Sobre el punto tenemos
Aplicamos la condición de equilibrio a cada cuerpo. Para la masa
Para el punto
Usando la condición dada por el enunciado, , y la ecuación (1), las ecuaciones (2) y (3) quedan
Dividiendo estas dos ecuaciones tenemos
Ahora sustituimos en (3) para obtener la tensión de la cuerda



















