Diferencia entre las páginas «Características cinemáticas de una partícula en movimiento, Septiembre 2016 (F1 G.I.C.)» y «Colisión inelástica sobre un muelle, Septiembre 2016 (F1 G.I.C.)»
(Página creada con «= Enunciado = (F1 G.I.C.)| Características cinemáticas de una partícula en movimiento ]] = Una partícula se mueve en el plano <math>OXY</math> de modo que su vector de posición <math>\overrightarrow{OP}</math> viene dado por la ley horaria <center> <math> \overrightarrow{OP}\equiv \vec{r}(t) = A\,\mathrm{sen}\,(\Omega t)\,\vec{\imath} - \dfrac{A}{2}\cos(2\Omega t)\,\vec{\jmath} </math> </center> siendo <math>A</math> y <math>\Omega</math> son constantes conoc…») |
(Página creada con «= Enunciado = right Una masa <math>m</math> se dirige hacia una masa <math>M</math> en reposo con velocidad de módulo <math>v_0</math>, como se indica en la figura. La masa <math>M</math> se encuentra conectada a un resorte ideal de constante elástica <math>k</math> y longitud natural <math>l_0</math>, anclado en el punto <math>O</math>. Antes de la colisión el muelle está relajado. El contacto con el suel…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | = Enunciado = | ||
[[Imagen:F1GIC_colision_inelastica_muelle_enunciado.png|right]] | |||
Una | Una masa <math>m</math> se dirige hacia una masa <math>M</math> en reposo con velocidad de módulo | ||
<math>\ | <math>v_0</math>, | ||
como se indica en la figura. La masa <math>M</math> se encuentra conectada a un resorte | |||
ideal de constante elástica <math>k</math> y longitud natural <math>l_0</math>, anclado en el punto | |||
<math>O</math>. Antes de la colisión | |||
el muelle está relajado. El contacto con el suelo es liso en todo momento. | |||
#Suponiendo que la colisión transcurre durante un tiempo <math>\Delta t</math> muy pequeño, y que es completamente inelástica, determina la velocidad de las dos masas justo después de la colisión. Calcula también la fuerza media ejercida sobre la masa <math>M</math> durante la colisión. | |||
#Supongamos a partir de ahora que las dos masas son iguales <math>M=m=m_0</math>. ¿Cuál es el valor mínimo de <math>v_0</math> para que las dos masas llegen hasta el eje <math>OY</math>? | |||
#Determina el vector de posición, la velocidad y la aceleración del conjunto formado por las dos masas para un instante de tiempo arbitrario después de la colisión. | |||
= Solución = | |||
== Colisión == | |||
El muelle no interviene en la colisión, pues al tener esta una duración temporal muy corta, no le da tiempo a comprimirse. La colisión es completamente inelástica. Sólo se conserva la cantidad de movimiento total del sistema. Y además sabemos que las dos masas quedan pegadas y tienen la misma velociad después del choque. La cantidad de movimiento antes del choque es | |||
<center> | |||
<math> | |||
\vec{P} = m\vec{v}_0 | |||
</math> | |||
</center> | |||
y después | |||
<center> | |||
<math> | |||
\vec{P} = (m+M)\,\vec{v}{\,'} | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{v}^{\,'} = \dfrac{m}{m+M}\,\vec{v}_0 = -\dfrac{m}{m+M}\,v_0\,\vec{\imath} | |||
</math> | |||
- | </center> | ||
\dfrac{ | La fuerza media sobre la masa <math>M </math> se obtiene de la variación de su cantidad de movimiento. Tenemos | ||
<center> | |||
<math> | |||
\Delta \vec{p}_M = \vec{F}_{m\to M}\Delta t | |||
</math> | |||
</center> | |||
y por otro lado | |||
<center> | |||
<math> | |||
\Delta\vec{p}_M = M\vec{v}^{\,'} - \vec{0} = -\dfrac{mM}{m+M}\,v_0\,\vec{\imath} | |||
</math> | |||
</center> | |||
Entonces | |||
<center> | |||
<math> | |||
\vec{F}_{m\to M} = -\dfrac{mM}{m+M}\,\dfrac{v_0}{\Delta t}\,\vec{\imath} | |||
</math> | </math> | ||
</center> | </center> | ||
= | == Condición para que lleguen al eje <math>OY </math>== | ||
Como no hay rozamiento, la energía mecánica se conserva. La energía potencial gravitatoria no cambia. La condición mínima es que las masas lleguen al punto <math>O </math> con velocidad nula. Entonces la energía cinética justo después de la colisión debe ser igual a la energía potencial elástica en el punto <math>O </math> | |||
<center> | |||
<math> | |||
\dfrac{1}{2}(2m_0)(v')^2 \geq \dfrac{1}{2}kl_0^2 | |||
\Longrightarrow | |||
|v'| \geq \sqrt{\dfrac{1}{2} \dfrac{kl_0^2}{m_0}} | |||
\Longrightarrow | |||
v_0\geq \sqrt{\dfrac{2kl_0^2}{m_0}} | |||
</math> | |||
</center> | |||
== | == Movimiento después de la colisión == | ||
Después de la colisión las masas realizan un movimiento oscilatorio uniforme. El movimiento es unidimensional sobre el eje <math>OX </math>. La reacción vincular de la superficie equilibra en todo momento el peso de las masas. De este modo, la ecuación de movimiento es | |||
<center><math> | <center> | ||
<math> | |||
(m+M)\vec{a} = -k(x-l_0)\,\vec{\imath} | |||
</math></center> | \Longrightarrow | ||
\ddot{x} = -\dfrac{k}{m+M}\,x + \dfrac{k}{m+M}l_0 | |||
<center><math> | </math> | ||
</center> | |||
\ | Describimos el movimiento respecto de la posición de equilibrio <math>x_{eq} = l_0 </math>. Definimos <math>s(t) </math> de modo que | ||
</math></center> | <center> | ||
<math> | |||
x(t) = l_0 + s(t) | |||
</math> | |||
</center> | |||
Sustituyendo en la ecuación de movimiento obtenemos la ecuación del MAS | |||
<center> | |||
<math> | |||
\ddot{s} = -\dfrac{k}{m+M}\,s | |||
</math> | |||
</center> | |||
Las soluciones pueden escribirse de la forma | |||
<center> | |||
<math> | |||
s(t) = A\cos(\omega t) + B\,\mathrm{sen}\,(\omega t) | |||
</math> | |||
</center> | |||
con la frecuencia angular | |||
<center> | |||
<math> | |||
\omega = \sqrt{\dfrac{k}{m+M}} \Longrightarrow | |||
T = \dfrac{2\pi}{\omega} = 2\pi\sqrt{\dfrac{m+M}{k}} | |||
</math> | |||
</center> | |||
siendo <math>T </math> el período de oscilación. | |||
== | Las condiciones iniciales del movimiento son | ||
<center> | |||
<center><math> | <math> | ||
s(0) = 0, \qquad \dot{s} = v'= - \dfrac{m}{m+M}\,v_0 | |||
</math></center> | </math> | ||
</center> | |||
A partir de la solución propuesta y su derivada obtenemos dos ecuaciones para <math>A </math> y <math>B </math> | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
s(0) = A = 0 \\ | |||
\\ | |||
\dot{s}(0) = B\omega = -\dfrac{m}{m+M}v_0 | |||
\Longrightarrow | |||
B = -\dfrac{mv_0}{\omega(m+M)} | |||
\end{array} | |||
</math> | |||
</center> | |||
Por lo tanto | |||
<center> | |||
<math> | |||
s(t) = -\dfrac{mv_0}{\omega(m+M)}\,\mathrm{sen}\,(\omega t) | |||
</math> | |||
</center> | |||
y | |||
<center> | <center> | ||
<math> | <math> | ||
x(t) = l_0 -\dfrac{mv_0}{\omega(m+M)}\,\mathrm{sen}\,(\omega t) | |||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría: | [[Categoría:Problemas de dinámica de la partícula|0]] | ||
[[Categoría:Problemas de | [[Categoría:Problemas de dinámica de la partícula]] | ||
[[Categoría:Problemas de examen de F1 GIC]] | [[Categoría:Problemas de examen de F1 GIC]] | ||
Revisión actual - 10:39 3 nov 2023
Enunciado
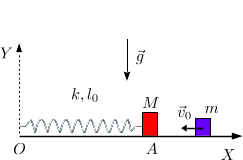
Una masa se dirige hacia una masa en reposo con velocidad de módulo , como se indica en la figura. La masa se encuentra conectada a un resorte ideal de constante elástica y longitud natural , anclado en el punto . Antes de la colisión el muelle está relajado. El contacto con el suelo es liso en todo momento.
- Suponiendo que la colisión transcurre durante un tiempo muy pequeño, y que es completamente inelástica, determina la velocidad de las dos masas justo después de la colisión. Calcula también la fuerza media ejercida sobre la masa durante la colisión.
- Supongamos a partir de ahora que las dos masas son iguales . ¿Cuál es el valor mínimo de para que las dos masas llegen hasta el eje ?
- Determina el vector de posición, la velocidad y la aceleración del conjunto formado por las dos masas para un instante de tiempo arbitrario después de la colisión.
Solución
Colisión
El muelle no interviene en la colisión, pues al tener esta una duración temporal muy corta, no le da tiempo a comprimirse. La colisión es completamente inelástica. Sólo se conserva la cantidad de movimiento total del sistema. Y además sabemos que las dos masas quedan pegadas y tienen la misma velociad después del choque. La cantidad de movimiento antes del choque es
y después
Por tanto
La fuerza media sobre la masa se obtiene de la variación de su cantidad de movimiento. Tenemos
y por otro lado
Entonces
Condición para que lleguen al eje
Como no hay rozamiento, la energía mecánica se conserva. La energía potencial gravitatoria no cambia. La condición mínima es que las masas lleguen al punto con velocidad nula. Entonces la energía cinética justo después de la colisión debe ser igual a la energía potencial elástica en el punto
Movimiento después de la colisión
Después de la colisión las masas realizan un movimiento oscilatorio uniforme. El movimiento es unidimensional sobre el eje . La reacción vincular de la superficie equilibra en todo momento el peso de las masas. De este modo, la ecuación de movimiento es
Describimos el movimiento respecto de la posición de equilibrio . Definimos de modo que
Sustituyendo en la ecuación de movimiento obtenemos la ecuación del MAS
Las soluciones pueden escribirse de la forma
con la frecuencia angular
siendo el período de oscilación.
Las condiciones iniciales del movimiento son
A partir de la solución propuesta y su derivada obtenemos dos ecuaciones para y
Por lo tanto
y






























