Diferencia entre las páginas «Archivo:F1GIC masa dos muelles enunciado.png» y «Colisión involucrando a tres partículas, Enero 2016 (F1 G.I.C.)»
Sin resumen de edición |
(Página creada con «== Enunciado == right Se tienen dos partículas de masa <math>m</math> (2 y 3) en reposo separadas por una cierta distancia. Otra partícula (1) de masa <math>m</math> se aproxima a una de ellas moviéndose sobre la recta que las une. La partícula 1 colisiona con la 2. Después de esta colisión, las partículas se mueven y se produce otra colisión con la partícula 3. Calcula la energía final de cada una de las tres pa…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | |||
[[Imagen:F1GIC_colision_tres_particulas.png|right]] | |||
Se tienen dos partículas de masa <math>m</math> (2 y 3) en reposo separadas por una cierta distancia. Otra partícula (1) de masa <math>m</math> se aproxima a una de ellas moviéndose sobre la recta que las une. La partícula 1 colisiona con la 2. Después de esta colisión, las partículas se mueven y se produce otra colisión con la partícula 3. Calcula la energía final de cada una de las tres partículas y la proporción de energía cinética inicial que se transmite a la partícula 3 en cada una de estas situaciones: | |||
#Todas las colisiones son elásticas. | |||
#La primera colisión es completamente inelástica y la segunda elástica. | |||
== Solución == | |||
=== Todas las colisiones elásticas === | |||
En todas las colisiones la cantidad de movimiento total del sistema se conserva. En las elásticas, además, se conserva la energía cinética total. En este problema tenemos dos colisiones consecutivas. Primero entre las partículas 1 y 2, y luego entre lo que resulte de esta colisión con la partícula 3 | |||
==== Colisión 1-2 ==== | |||
Examinemos la cantidad de movimiento. Antes de la colisión tenemos | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}_1 = mv_0\,\vec{\imath}\\ | |||
\vec{p}_2 = \vec{0} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P} = \vec{p}_1 + \vec{p}_2 = mv_0\,\vec{\imath} | |||
</math> | |||
</center> | |||
Después de la colisión, la cantidad de movimiento es | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}{\,'}_1 = mv_1'\,\vec{\imath}\\ | |||
\vec{p}{\,'}_2 = mv_2'\,\vec{\imath} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P}{\,'} = \vec{p}{\,'}_1 + \vec{p}{\,'}_2 = m(v_1' + v_2')\,\vec{\imath} | |||
</math> | |||
</center> | |||
Igualando la cantidad de movimiento antes y después tenemos | |||
<center> | |||
<math> | |||
v_1' + v_2' = v_0 | |||
</math> | |||
</center> | |||
Examinemos ahora la energía cinética. Antes del choque | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}mv_0^2 | |||
</math> | |||
</center> | |||
Después del choque | |||
<center> | |||
<math> | |||
T' = \dfrac{1}{2}m(v_1')^2 + \dfrac{1}{2}m(v_2')^2 | |||
</math> | |||
</center> | |||
Igualando tenemos | |||
<center> | |||
<math> | |||
v_0^2 = (v_1')^2 + (v_2')^2 | |||
</math> | |||
</center> | |||
Resolviendo tenemos | |||
<center> | |||
<math> | |||
v_1' = 0, \qquad v_2' = v_0 | |||
</math> | |||
</center> | |||
La primera partícula se queda quieta y la segunda parte con la misma velocidad que traía la primera | |||
==== Colisión 2-3 ==== | |||
Como todas las partículas tienen la misma masa, esta colisión es una repetición exacta de la primera. El resultado final es que la partícula 2 se queda quieta y la 3 sale con la velocidad que tenía la 2, es decir, la velocidad de la partícula 1 antes de la primera colisión. El esta final del sistema es | |||
<center> | |||
<math> | |||
\vec{v}_1^{\,'} = \vec{v}_2^{\,'} = \vec{0}, \qquad \vec{v}_3^{\,'}=v_0\,\vec{\imath} | |||
</math> | |||
</center> | |||
La energía cinética de la partícula 3 es la misma que tenía al principio la partícula 1. Es decir, se ha producido una transferencia de energía del 100% | |||
=== Primera colisión plástica y la segunda elástica === | |||
En todas las colisiones se conserva la cantidad de movimiento global. Pero en una colisión plástica no se conserva la energía cinética global. La condición que hay que imponer es que las partículas participantes en la colisión quedan unidas después, y tienen por tanto la misma velocidad. | |||
==== Colisión 1-2 ==== | |||
Examinemos la cantidad de movimiento. Antes de la colisión tenemos | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}_1 = mv_0\,\vec{\imath}\\ | |||
\vec{p}_2 = \vec{0} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P} = \vec{p}_1 + \vec{p}_2 = mv_0\,\vec{\imath} | |||
</math> | |||
</center> | |||
Después de la colisión, la cantidad de movimiento es | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}{\,'}_1 = mv_1'\,\vec{\imath}\\ | |||
\vec{p}{\,'}_2 = mv_1'\,\vec{\imath} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P}{\,'} = \vec{p}{\,'}_1 + \vec{p}{\,'}_2 = 2mv_1'\,\vec{\imath} | |||
</math> | |||
</center> | |||
Hemos usado la condición de que la velocidad de las partículas es la misma después de la colisión. | |||
Igualando la cantidad de movimiento antes y después tenemos | |||
<center> | |||
<math> | |||
2v_1 = v_0 \Longrightarrow v_1' = v_2' = v_0/2 | |||
</math> | |||
</center> | |||
==== Colisión 2-3 ==== | |||
Ahora tenemos una colisión de una partícula de masa <math>2m </math> (las partículas 1 y 2 unidas) y con velocidad <math>(v_0/2)\,\vec{\imath} </math> con la partícula 3, de masa <math>m </math> y en reposo. Al ser elástica, se conservan tanto la cantidad de movimiento como la energía cinética. | |||
Examinemos la cantidad de movimiento. Antes de la colisión tenemos | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}_{12} = 2m(v_0/2)\,\vec{\imath}= mv_0\,\vec{\imath}\\ | |||
\vec{p}_3 = \vec{0} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P} = \vec{p}_{12} + \vec{p}_3 = mv_0\,\vec{\imath} | |||
</math> | |||
</center> | |||
Después de la colisión, la cantidad de movimiento es | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
\vec{p}{\,'}_{12} = 2mv_{12}'\,\vec{\imath}\\ | |||
\vec{p}{\,'}_3 = mv_3'\,\vec{\imath} | |||
\end{array} | |||
\right\} | |||
\Longrightarrow | |||
\vec{P}{\,'} = \vec{p}{\,'}_{12} + \vec{p}{\,'}_3 = m(2v_{12}' + v_2')\,\vec{\imath} | |||
</math> | |||
</center> | |||
Igualando la cantidad de movimiento antes y después tenemos | |||
<center> | |||
<math> | |||
2v_{12}' + v_3' = v_0 | |||
</math> | |||
</center> | |||
Examinemos ahora la energía cinética. Antes del choque | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}(2m)(v_0/2)^2=\dfrac{1}{4}mv_0^2 | |||
</math> | |||
</center> | |||
Después del choque | |||
<center> | |||
<math> | |||
T' = \dfrac{1}{2}(2m)(v_{12}')^2 + \dfrac{1}{2}m(v_3')^2 | |||
= m(v_{12}')^2 + \dfrac{1}{2}m(v_3')^2 | |||
</math> | |||
</center> | |||
Igualando tenemos | |||
<center> | |||
<math> | |||
\dfrac{1}{4}v_0^2 = (v_{12}')^2 + \dfrac{1}{2}(v_3')^2 | |||
</math> | |||
</center> | |||
Resolviendo tenemos | |||
<center> | |||
<math> | |||
v_{12}' = \dfrac{1}{6}v_0, \qquad v_3' = \dfrac{2}{3}v_0 | |||
</math> | |||
</center> | |||
La energía cinética final de la partícula 3 es | |||
<center> | |||
<math> | |||
T_3' = \dfrac{1}{2}m(v_3')^2 = \dfrac{4}{9}\left(\dfrac{1}{2}mv_0^2\right) | |||
= \dfrac{4}{9}T_0 | |||
</math> | |||
</center> | |||
Por tanto la energía transferida a ala partícula 3 es (4/9)=44% de la original. | |||
[[Categoría:Problemas de sistemas de partículas]] | |||
[[Categoría:Problemas de examen]] | |||
[[Categoría:Problemas de examen de F1 GIC]] | |||
Revisión actual - 10:34 3 nov 2023
Enunciado

Se tienen dos partículas de masa (2 y 3) en reposo separadas por una cierta distancia. Otra partícula (1) de masa se aproxima a una de ellas moviéndose sobre la recta que las une. La partícula 1 colisiona con la 2. Después de esta colisión, las partículas se mueven y se produce otra colisión con la partícula 3. Calcula la energía final de cada una de las tres partículas y la proporción de energía cinética inicial que se transmite a la partícula 3 en cada una de estas situaciones:
- Todas las colisiones son elásticas.
- La primera colisión es completamente inelástica y la segunda elástica.
Solución
Todas las colisiones elásticas
En todas las colisiones la cantidad de movimiento total del sistema se conserva. En las elásticas, además, se conserva la energía cinética total. En este problema tenemos dos colisiones consecutivas. Primero entre las partículas 1 y 2, y luego entre lo que resulte de esta colisión con la partícula 3
Colisión 1-2
Examinemos la cantidad de movimiento. Antes de la colisión tenemos
Después de la colisión, la cantidad de movimiento es
Igualando la cantidad de movimiento antes y después tenemos
Examinemos ahora la energía cinética. Antes del choque
Después del choque
Igualando tenemos
Resolviendo tenemos
La primera partícula se queda quieta y la segunda parte con la misma velocidad que traía la primera
Colisión 2-3
Como todas las partículas tienen la misma masa, esta colisión es una repetición exacta de la primera. El resultado final es que la partícula 2 se queda quieta y la 3 sale con la velocidad que tenía la 2, es decir, la velocidad de la partícula 1 antes de la primera colisión. El esta final del sistema es
La energía cinética de la partícula 3 es la misma que tenía al principio la partícula 1. Es decir, se ha producido una transferencia de energía del 100%
Primera colisión plástica y la segunda elástica
En todas las colisiones se conserva la cantidad de movimiento global. Pero en una colisión plástica no se conserva la energía cinética global. La condición que hay que imponer es que las partículas participantes en la colisión quedan unidas después, y tienen por tanto la misma velocidad.
Colisión 1-2
Examinemos la cantidad de movimiento. Antes de la colisión tenemos
Después de la colisión, la cantidad de movimiento es
Hemos usado la condición de que la velocidad de las partículas es la misma después de la colisión. Igualando la cantidad de movimiento antes y después tenemos
Colisión 2-3
Ahora tenemos una colisión de una partícula de masa (las partículas 1 y 2 unidas) y con velocidad con la partícula 3, de masa y en reposo. Al ser elástica, se conservan tanto la cantidad de movimiento como la energía cinética.
Examinemos la cantidad de movimiento. Antes de la colisión tenemos
Después de la colisión, la cantidad de movimiento es
Igualando la cantidad de movimiento antes y después tenemos
Examinemos ahora la energía cinética. Antes del choque
Después del choque
Igualando tenemos
Resolviendo tenemos
La energía cinética final de la partícula 3 es
Por tanto la energía transferida a ala partícula 3 es (4/9)=44% de la original.
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 10:34 3 nov 2023 | 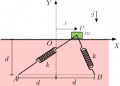 | 275 × 197 (17 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:




















