Diferencia entre las páginas «Archivo:F1GIC BarraParAplicado Enunciado02.png» y «Barra articulada con momento aplicado, Enero 2016 (G.I.C.)»
Sin resumen de edición |
(Página creada con «= Enunciado = right En el sistema de la figura, la barra <math>\overline{OA}</math> (sólido "2") tiene masa <math>m</math> y longitud <math>2L</math>. La barra está articulada en el punto fijo <math>O</math> de una barra vertical fija(sólido "1"). Se aplica un par <math>\vec{\tau}=\tau_0\,\vec{k}</math> sobre la barra "2". El sistema está sometido a la gravedad. #¿Como debe ser el par aplicado para que el ángu…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Imagen:F1GIC_BarraParAplicado_Enunciado01.png|right]] | |||
En el sistema de la figura, la barra <math>\overline{OA}</math> (sólido "2") tiene masa <math>m</math> y longitud | |||
<math>2L</math>. La barra está articulada en el punto fijo <math>O</math> de una barra vertical fija(sólido "1"). Se aplica un par <math>\vec{\tau}=\tau_0\,\vec{k}</math> sobre la barra "2". El sistema está sometido a la gravedad. | |||
#¿Como debe ser el par aplicado para que el ángulo sea <math>\theta_1=\pi/6</math>? | |||
#Ahora, manteniendo aplicado el par de la pregunta anterior, se apoya una barra homogénea "0", de masa <math>m</math> y longitud <math>2L</math>, como se indica en la figura. La barra "0" se mantiene siempre horizontal. Todos los contactos son lisos. | |||
#¿Cuanto vale el ángulo de equilibrio en la nueva situación? | |||
#Calcula el par vincular sobre la barra "0" originado por el vínculo en <math>B</math> es | |||
= Solución = | |||
== Par para mantener el equilibrio == | |||
[[Imagen:F1GIC_BarraParAplicado_Fuerzas01.png|right|300ppx]] | |||
La imagen de la derecha muestra el diagrama de cuerpo libre del sólido "0". Hay una fuerza vincular en <math>O</math> con tres posibles componentes no nulas, pues el punto <math>O</math> está fijo. Las fuerzas y pares son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{P} = -mg\,\vec{\jmath}\\ | |||
\vec{\Phi}^{\,O}_{1\to2} = O_x\,\vec{\imath} + O_y\,\vec{\jmath} + O_z\,\vec{k}\\ | |||
\vec{\tau} = \tau_0\,\vec{k} | |||
\end{array} | |||
</math> | |||
</center> | |||
La suma de fuerzas debe ser cero | |||
<center> | |||
<math> | |||
\vec{P} + \vec{\Phi}^{\,O}_{1\to2} = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
(X) & \to & O_x=0 & (1)\\ | |||
(Y) & \to & O_y=mg& (2)\\ | |||
(Z) & \to & O_z=0 & (3) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
El momento neto respecto a <math>O</math> debe ser cero | |||
<center> | |||
<math> | |||
\vec{M}_O = \vec{\tau} + \overrightarrow{OG_2}\times\vec{P} = \vec{0} | |||
</math> | |||
</center> | |||
El momento ejercido por el peso es | |||
<center> | |||
<math> | |||
\overrightarrow{OG_2}\times\vec{P} = | |||
(L\,\mathrm{sen}\,\theta_1\,\vec{\imath} + L\cos\theta_1\,\vec{\jmath})\times(-mg\,\vec{\jmath}) | |||
= | |||
-mgL\,\mathrm{sen}\,\theta\,\vec{k} | |||
</math> | |||
</center> | |||
La ecuación del momento nos da la ecuación | |||
<center> | |||
<math> | |||
\tau_0 - mgL\,\mathrm{sen}\,\theta_1 = 0, \qquad\qquad (4) | |||
</math> | |||
</center> | |||
De aquí obtenemos el valor del par | |||
<center> | |||
<math> | |||
\vec{\tau} = mgL\,\mathrm{sen}\,\theta_1 \,\vec{k} = \dfrac{1}{2}mgL\,\vec{k} | |||
</math> | |||
</center> | |||
== Con barra horizontal aplicada == | |||
[[Imagen:F1GIC_BarraParAplicado_Fuerzas02.png|right|300ppx]] | |||
La imagen de la derecha muestra el diagrama de cuerpo libre de ambos sólidos. Hay una fuerza vincular en <math>O</math> sobre el "2" con tres posibles componentes no nulas, pues el punto <math>O</math> está fijo. En el punto <math>A</math> las fuerzas vinculares forman un par de acción reacción. En el punto <math>B</math> hay una fuerza vincular sobre "0" para impedir un desplazamiento que no sea en la dirección del eje <math>Y_1</math>. También hay un par vincular para que no haya rotación de la barra "0". | |||
Las expresiones de fuerzas y pares sobre el sólido "2" son | |||
Las fuerzas y pares son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{P}_2 = -mg\,\vec{\jmath}\\ | |||
\vec{\Phi}^{\,O}_{1\to2} = O_x\,\vec{\imath} + O_y\,\vec{\jmath} + O_z\,\vec{k}\\ | |||
\vec{\Phi}^{\,A}_{0\to2} = -A_y\,\vec{\jmath} \\ | |||
\vec{\tau} = \tau_0\,\vec{k} | |||
\end{array} | |||
</math> | |||
</center> | |||
Sobre el sólido "0" tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{P}_0 = -mg\,\vec{\jmath}\\ | |||
\vec{\Phi}^{\,A}_{2\to0} = A_y\,\vec{\jmath} \\ | |||
\vec{\Phi}^{\,B}_{1\to0} = B_x\,\vec{\imath} + B_z\,\vec{k}\\ | |||
\vec{\Gamma}_{1\to0} = \Gamma\,\vec{k} | |||
\end{array} | |||
</math> | |||
</center> | |||
Aplicamos la condiciones de equilibrio para cada sólido. Para el sólido "2" | |||
<center> | |||
<math> | |||
\vec{P}_2 + \vec{\Phi}^{\,O}_{1\to2} + \vec{\Phi}^{\,A}_{0\to2} = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
(X) & \to & O_x=0 & (1)\\ | |||
(Y) & \to & O_y-A_y=mg& (2)\\ | |||
(Z) & \to & O_z=0 & (3) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
El momento respecto a <math>O</math> debe ser cero | |||
<center> | |||
<math> | |||
\vec{M}_O = \vec{\tau} + \overrightarrow{OG_2}\times\vec{P}_2 + \overrightarrow{OA}\times\vec{\Phi}^{\,A}_{0\to2} = \vec{0} | |||
\Longrightarrow | |||
\tau_0 - mgL\,\mathrm{sen}\,\theta -2A_yL\,\mathrm{sen}\,\theta = 0\, \qquad(4) | |||
</math> | |||
</center> | |||
La fuerza neta sobre el sólido "0" debe ser cero | |||
<center> | |||
<math> | |||
\vec{P}_0 + \vec{\Phi}^{\,B}_{1\to0} + \vec{\Phi}^{\,A}_{2\to0} = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
(X) & \to & B_x=0 & (5)\\ | |||
(Y) & \to & A_y=mg& (6)\\ | |||
(Z) & \to & B_z=0 & (7) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Calculamos el momento neto respecto a <math>B</math> | |||
<center> | |||
<math> | |||
\vec{M}_B = \overrightarrow{BG}_0\times\vec{P}_0 + \overrightarrow{BA}\times\vec{\Phi}^{\,A}_{2\to0} + \vec{\Gamma}_{1\to0}=\vec{0} | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\overrightarrow{BG}_0\times\vec{P}_0 = | |||
(L\,\vec{\imath})\times(-mg\,\vec{\jmath}) = -mgL\,\vec{k} \\ | |||
\overrightarrow{BA}\times\vec{\Phi}^{\,A}_{2\to0} = | |||
(2L\,\mathrm{sen}\,\theta\,\vec{\imath})\times(A_y\,\vec{\jmath})= | |||
2LA_y\,\mathrm{sen}\,\theta\,\vec{k} | |||
\end{array} | |||
</math> | |||
</center> | |||
Entonces | |||
<center> | |||
<math> | |||
\Gamma - mgL + 2LA_y\,\mathrm{sen}\,\theta = 0. \qquad (8) | |||
</math> | |||
</center> | |||
Tenemos 8 ecuaciones para 8 incógnitas, a saber <math>\{O_x, O_y, O_z, A_y, B_x, B_z, \Gamma, \theta\}</math>. Resolviendo tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\Phi}^{\,O}_{1\to2} = 2mg\,\vec{\jmath},\\ | |||
\vec{\Phi}^{\,A}_{2\to0} = mg\,\vec{\jmath},\\ | |||
\vec{\Phi}^{\,B}_{1\to0} = \vec{0}\\ | |||
\\ | |||
\vec{\Gamma}_{1\to0} = \dfrac{2}{3}mgL\,\vec{k}\\ | |||
\mathrm{sen}\,\theta = \dfrac{\tau_0}{3mgL} = \dfrac{1}{6} | |||
\end{array} | |||
</math> | |||
</center> | |||
[[Categoría: Problemas de Estática]] | |||
[[Categoría: Problemas de Estática del Sólido Rígido]] | |||
[[Categoría:Problemas de examen de F1 GIC]] | |||
Revisión actual - 10:32 3 nov 2023
Enunciado
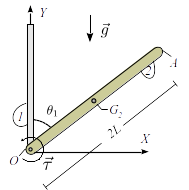
En el sistema de la figura, la barra (sólido "2") tiene masa y longitud . La barra está articulada en el punto fijo de una barra vertical fija(sólido "1"). Se aplica un par sobre la barra "2". El sistema está sometido a la gravedad.
- ¿Como debe ser el par aplicado para que el ángulo sea ?
- Ahora, manteniendo aplicado el par de la pregunta anterior, se apoya una barra homogénea "0", de masa y longitud , como se indica en la figura. La barra "0" se mantiene siempre horizontal. Todos los contactos son lisos.
- ¿Cuanto vale el ángulo de equilibrio en la nueva situación?
- Calcula el par vincular sobre la barra "0" originado por el vínculo en es
Solución
Par para mantener el equilibrio
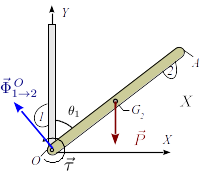
La imagen de la derecha muestra el diagrama de cuerpo libre del sólido "0". Hay una fuerza vincular en con tres posibles componentes no nulas, pues el punto está fijo. Las fuerzas y pares son
La suma de fuerzas debe ser cero
El momento neto respecto a debe ser cero
El momento ejercido por el peso es
La ecuación del momento nos da la ecuación
De aquí obtenemos el valor del par
Con barra horizontal aplicada
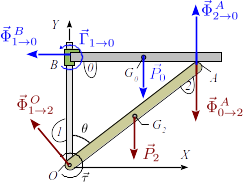
La imagen de la derecha muestra el diagrama de cuerpo libre de ambos sólidos. Hay una fuerza vincular en sobre el "2" con tres posibles componentes no nulas, pues el punto está fijo. En el punto las fuerzas vinculares forman un par de acción reacción. En el punto hay una fuerza vincular sobre "0" para impedir un desplazamiento que no sea en la dirección del eje . También hay un par vincular para que no haya rotación de la barra "0".
Las expresiones de fuerzas y pares sobre el sólido "2" son Las fuerzas y pares son
Sobre el sólido "0" tenemos
Aplicamos la condiciones de equilibrio para cada sólido. Para el sólido "2"
El momento respecto a debe ser cero
La fuerza neta sobre el sólido "0" debe ser cero
Calculamos el momento neto respecto a
Tenemos
Entonces
Tenemos 8 ecuaciones para 8 incógnitas, a saber . Resolviendo tenemos
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 10:31 3 nov 2023 |  | 189 × 194 (19 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:
























