(Página creada con «= Enunciado = right Una partícula de masa <math>10m_0</math> desliza sin rozamiento sobre un semidisco de radio <math>R</math>. En el instante inicial la partícula se encuentra en el punto <math>A</math> y se le imparte una velocidad horizontal de rapidez <math>v_0=\lambda\sqrt{gR}</math>, siendo <math>\lambda</math> un número real positivo. La masa está conectada a un muelle de constante elástica <math>k=25m_0g/…»)
 
(Página creada con «==Enunciado== Sea <math>r\,</math> la recta que pasa por el punto <math>P_1\,</math> y es paralela al vector <math>\vec{u}\,</math>, y sea <math>P_2\,</math> un punto que no pertenece a <math>r\,</math>. ¿Cuál es el lugar geométrico de los puntos <math>P\,</math> que satisfacen la ecuación <math>\overrightarrow{P_1P}\cdot\vec{u}=\overrightarrow{P_1P_2}\cdot\vec{u}\,</math>? ==Solución== Como aplicación del producto escalar de vectores, se ha estudiado en la teo…»)
 
Línea 1: Línea 1:
= Enunciado =
==Enunciado==
[[File:F1GIC-particulaDiscoMuelle-enunciado.png|right]]
Sea <math>r\,</math> la recta que pasa por el punto <math>P_1\,</math> y es paralela al vector <math>\vec{u}\,</math>, y sea <math>P_2\,</math> un punto que no pertenece a <math>r\,</math>.
Una partícula de masa <math>10m_0</math> desliza sin rozamiento sobre un semidisco de radio <math>R</math>. En el instante inicial la partícula se encuentra en el punto <math>A</math> y se le imparte una velocidad horizontal de rapidez <math>v_0=\lambda\sqrt{gR}</math>, siendo <math>\lambda</math> un número real positivo.  La masa está conectada a un muelle de constante elástica <math>k=25m_0g/R</math> y longitud natural nula. El otro extremo del muelle está conectado al punto <math>B</math> que se mueve de modo que el muelle permanece siempre horizontal.
#Escribe los vectores de la base cartesiana en la base polar.
#Escribe la expresión de la fuerza ejercida por el muelle sobre la masa en la base polara.
#Escribe la expersión que da la velocidad de la partícula para el ángulo <math>\theta=\beta</math>, con <math>\mathrm{sen}\,\beta=3/5</math> y <math>\cos\beta=4/5</math>.
#¿Que condición debe cumplir <math>\lambda</math> para que la partícula se separe del disco en ese ángulo <math>\beta</math>?


= Solución =
¿Cuál es el lugar geométrico de los puntos <math>P\,</math> que satisfacen la ecuación <math>\overrightarrow{P_1P}\cdot\vec{u}=\overrightarrow{P_1P_2}\cdot\vec{u}\,</math>?
==Solución==
Como aplicación del producto escalar de vectores, se ha estudiado en la teoría que la ecuación del plano perpendicular al vector <math>\vec{N}\,</math> y que pasa por el punto <math>Q\,</math> viene dada por:
<center><math>\overrightarrow{QP}\cdot\vec{N}=0</math></center>
Pues bien, la ecuación que nos propone el enunciado del presente ejercicio se reduce a esta forma mediante una sencilla operación de resta:
<center><math>\overrightarrow{P_1P}\cdot\vec{u}=\overrightarrow{P_1P_2}\cdot\vec{u}\,\,\,\,\,\longrightarrow\,\,\,\,\,\left(\overrightarrow{P_1P}-\overrightarrow{P_1P_2}\right)\cdot\vec{u}=0\,\,\,\,\,\longrightarrow\,\,\,\,\,\overrightarrow{P_2P}\cdot\vec{u}=0</math></center>
Por tanto, el lugar geométrico de los puntos <math>P\,</math> que satisfacen dicha ecuación es el plano perpendicular a la recta <math>r\,</math> y que pasa por el punto <math>P_2\,</math> (nótese que <math>r\,</math> es paralela a <math>\vec{u}\,</math>).


'''Vectores cartesianos en la base polar '''
==Solución alternativa==
[[Archivo:Plano-vectorial-02.png|right]]


Observando los vectores de la base indicados en la figura del enunciado tenemos
La ecuación vectorial de un plano perpendicular al vector <math>\vec{B}</math> es de la forma general
<center>
<math>
\begin{array}{l}
\vec{\imath} = \cos\theta\,\vec{u}_r - \mathrm{sen}\,\theta\,\vec{u}_{\theta},\\
\vec{\jmath} = \mathrm{sen}\,\theta\,\vec{u}_r + \cos\theta\,\vec{u}_{\theta}.
\end{array}
</math>
</center>


''' Fuerza ejercida por el muelle '''
<center><math>\overrightarrow{AP}\cdot \vec{B}=k</math></center>


Dado que tiene longitud natural nula la fuerza ejercida por el muelle puede escribirse
siendo A un punto fijo y <math>k</math> una constante. Tomando distintos valores de <math>k</math> obtenemos planos paralelos.
<center>
<math>
\vec{F}_k = -k\,\overrightarrow{BC}.
</math>
</center>
Tenemos
<center>
<math>
\overrightarrow{BC} = \overline{BC}\,\vec{\imath} = R\cos\theta\,\vec{\imath}.
</math>
</center>
Utilizando la expresión de <math>\vec{\imath}</math> del apartado anterior tenemos
<center>
<math>
\vec{F}_k = -kR\cos^2\theta\,\vec{u}_r + kR\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta}
= -25m_0g\cos^2\theta\,\vec{u}_r + 25m_0g\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta}.
</math>
</center>


''' Expresión de la velocidad de la partícula '''
En nuestro caso la ecuación tiene esta forma si tomamos <math>\vec{B}=\vec{u}</math>. Es decir se trata de un plano perpendicular al vector <math>\vec{u}</math> y por tanto a la recta <math>r</math>.
 
Como el vínculo es liso, las únicas fuerzas que hacen trabajo son las debidas a la gravedad y al muelle, que son conservativas. Por tanto la energía mecánica se conserva. En el punto <math>A</math> vale
<center>
<math>
E_A = \dfrac{1}{2}mv_A^2 + mgR = 5m_0gR\lambda^2 + 10m_0gR.
</math>
</center>
Hemos escogido como altura de referencia para la energía potencial la de la base del semidisco. Para el ángulo <math>\beta</math> tenemos
<center>
<math>
E = \dfrac{1}{2}mv^2 + mgR\mathrm{sen}\,\beta + \dfrac{1}{2}k(R\cos\beta)^2 =
5m_0v_{\beta}^2 + 14m_0gR.
=
</math>
</center>
Evaluando para <math>\theta=\beta</math> e igualando las dos expresiones obtenemos
<center>
<math>
v_{\beta} = \sqrt{\dfrac{gR}{5}}\,\sqrt{5\lambda^2-4}
</math>
</center>


''' Condición para que la partícula se separe de la superficie '''
Para hallar un punto de este plano simplemente observamos que la ecuación se cumple para <math>P=P_2</math> ya que trivialmente


Cuando la partícula se separa la normal que ejerce la superficie sobre ella se anula, pues ya no es necesaria para que la partícula no penetre en el disco. Las fuerzas que actúan sobre la partícula son, en la base polar
<center><math>P=P_2\qquad\Rightarrow\qquad \overrightarrow{P_1P_2}\cdot\vec{u}=\overrightarrow{P_1P_2}\cdot\vec{u}\,</math>
<center>
<math>
\begin{array}{l}
\vec{P} = -mg\,\vec{\jmath} = -10m_0g\,\mathrm{sen}\,\theta\,\vec{u}_r - 10m_0g\cos\theta\,\vec{u}_{\theta},\\
\vec{N} = N\,\vec{u}_r,\\
\vec{F}_k = -25m_0g\cos^2\theta\,\vec{u}_r + 25m_0g\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta}.
\end{array}
</math>
</center>
La aceleración de la partícula es
<center>
<math>
\vec{a} = -R\dot{\theta}^2\,\vec{u}_r + R\ddot{\theta}\,\vec{u}_{\theta}.
</math>
</center>
A partir de la Segunda Ley de Newton obtenemos
<center>
<math>
m\vec{a} = \vec{P} + \vec{N} + \vec{F}_k
\to
\left\{
\begin{array}{lr}
-10m_0R\dot{\theta}^2 = -10m_0g\,\mathrm{sen}\,\theta - 25m_0g\cos^2\theta + N, & (1)\\
10m_0\ddot{\theta} = -10m_0g\cos\theta + 25m_0g\,\mathrm{sen}\,\theta\cos\theta. & (2)
\end{array}
\right.
</math>
</center>
De la primera ecuación obtenemos
<center>
<math>
N = -10m_0R\dot{\theta}^2 + 10m_0g\,\mathrm{sen}\,\theta +  25m_0g\cos^2\theta.
</math>
</center>
La velocidad de la partícula es
<center>
<math>
\vec{v} = R\dot{\theta}\,\vec{u}_{\theta},
</math>
</center>
por lo que la normal puede escribirse
<center>
<math>
N = -10m_0\dfrac{v^2}{R} + 10m_0g\,\mathrm{sen}\,\theta +  25m_0g\cos^2\theta.
</math>
</center>
Imponiendo que sea cero cuando <math>\theta=\beta</math> obtenemos la condición
<center>
<math>
\lambda=\sqrt{3}.
</math>
</center>
</center>
Por tanto, se trata de un plano perpendicular a la recta r y que pasa por el punto <math>P_2</math>.


[[Categoría:Problemas de Dinámica de la partícula]]
[[Categoría:Problemas de Vectores Libres (GITI)]]
[[Categoría:Problemas de Cinética de la partícula]]
[[Categoría:Dinámica del punto material|1]]

Revisión del 13:14 9 ene 2024

Enunciado

Sea la recta que pasa por el punto y es paralela al vector , y sea un punto que no pertenece a .

¿Cuál es el lugar geométrico de los puntos que satisfacen la ecuación ?

Solución

Como aplicación del producto escalar de vectores, se ha estudiado en la teoría que la ecuación del plano perpendicular al vector y que pasa por el punto viene dada por:

Pues bien, la ecuación que nos propone el enunciado del presente ejercicio se reduce a esta forma mediante una sencilla operación de resta:

Por tanto, el lugar geométrico de los puntos que satisfacen dicha ecuación es el plano perpendicular a la recta y que pasa por el punto (nótese que es paralela a ).

Solución alternativa

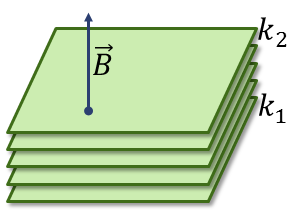
La ecuación vectorial de un plano perpendicular al vector es de la forma general

siendo A un punto fijo y una constante. Tomando distintos valores de obtenemos planos paralelos.

En nuestro caso la ecuación tiene esta forma si tomamos . Es decir se trata de un plano perpendicular al vector y por tanto a la recta .

Para hallar un punto de este plano simplemente observamos que la ecuación se cumple para ya que trivialmente

Por tanto, se trata de un plano perpendicular a la recta r y que pasa por el punto .

Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_deslizando_sobre_disco_con_muelle_(Ene._2021_G.I.C.)&oldid=2618»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_deslizando_sobre_disco_con_muelle_(Ene._2021_G.I.C.)&oldid=2618»