Triciclo (MR G.I.C.)

Enunciado

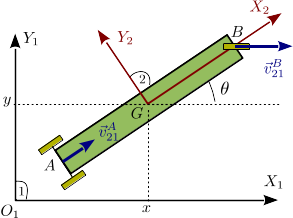
El sistema de la figura representa un modelo muy simple de triciclo. Está formado por una barra homogénea ${\overline {AB}}$ (sólido "2", masa $m$, longitud $l=2a$, centro de masas $G$) contenida en el plano horizontal $OX_{1}Y_{1}$ y obligada a moverse de modo que su extremo $A$ tiene una velocidad apuntando a $B$, mientras que la velocidad de $B$ se mantiene siempre paralela al eje $OX_{1}$. Se propone trabajar con las coordenadas generalizadas $\{x,y,\theta \}$ indicadas en la figura.

1. Demuestra que las condiciones de movimiento implican las siguientes ecuaciones de ligadura para los puntos $A$ y $B$: $\{a_{1}\operatorname {sen} \theta {\dot {x}}+a_{2}\cos \theta {\dot {y}}+a_{3}{\dot {\theta }}=0;\,b_{1}{\dot {x}}+b_{2}{\dot {y}}+b_{3}{\dot {\theta }}\cos \theta =0\}$, donde $\{a_{i},b_{i}\}$ son constantes a determinar.
2. Desarrolla las ecuaciones de Lagrange con ligaduras correspondientes al sistema mecánico.
3. Calcula los valores de las fuerzas vinculares $\{{\vec {A}},{\vec {B}}\}$ responsables de las ligaduras del primer apartado en función de los multiplicadores de Lagrange del problema.

Solución

Reducción cinemática

El vector rotación es

${\vec {\omega }}_{21}={\dot {\theta }}\,{\vec {k}}.$

La velocidad en el centro de masas $G$ es

${\vec {v}}_{21}^{\,G}={\dot {x}}\,{\vec {\imath }}_{1}+{\dot {y}}\,{\vec {\jmath }}_{1}.$

Ligaduras

La ligadura en el punto $A$ implica que la velocidad ${\vec {v}}_{21}^{\,A}$ tiene que ser paralela al vector ${\overrightarrow {AB}}$. Este vector es

${\overrightarrow {AB}}=2a\cos \theta \,{\vec {\imath }}_{1}+2a\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}.$

Usando el teorema de Chasles a partir de $G$ la velocidad en $A$ es

${\vec {v}}_{21}^{\,A}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GA}}=({\dot {x}}+a{\dot {\theta }}\mathrm {sen} \,\theta )\,{\vec {\imath }}_{1}+({\dot {y}}-a{\dot {\theta }}\cos \theta )\,{\vec {\jmath }}_{1},$

donde hemos usado ${\overrightarrow {GA}}=-a\cos \theta \,{\vec {\imath }}_{1}-a\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}$.

Por tanto la ligadura puede aplicarse exigiendo que

${\vec {v}}_{21}^{\,A}\times {\overrightarrow {AB}}={\vec {0}}\Longrightarrow {\dot {x}}\,\mathrm {sen} \,\theta -{\dot {y}}\cos \theta +a{\dot {\theta }}=0.$

Esta es una ligadura cinemática no integragble, es decir, es no holónoma.

La ligadura en $B$ implica que

${\vec {v}}_{21}^{\,B}\parallel {\vec {\imath }}_{1}.$

Usando el teorema de Chasles desde $G$ tenemos

${\vec {v}}_{21}^{\,B}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GB}}=({\dot {x}}-a{\dot {\theta }}\mathrm {sen} \,\theta )\,{\vec {\imath }}_{1}+({\dot {y}}+a{\dot {\theta }}\cos \theta )\,{\vec {\jmath }}_{1},$

donde hemos usado ${\overrightarrow {GB}}=a\cos \theta \,{\vec {\imath }}_{1}+a\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}$.

Entonces

${\vec {v}}_{21}^{\,B}\parallel {\vec {\imath }}_{1}\Longrightarrow {\dot {y}}+a{\dot {\theta }}\cos \theta =0.$

Esta ligadura es cinemática integrable, es decir es holónoma.

Como hay dos ligaduras y es un movimiento plano, el sistema tiene sólo un grado de libertad. Lo que es curioso en este problema es, que aunque la ligadura en $A$ es, por si sola, no holónoma, combinada con la ligadura en $B$ sí que se puede integrar. Es decir el problema es holónomo. Sin embargo, esta integración es complicada. Por ello, aunque el sistema puede tiene sólo un grado de libertad, vamos a trabajar con las tres coordenadas $\{x,y,\theta \}$. Usaremos multiplicadores de Lagrange para poder utlizar las dos coordenadas extras respecto al número de grados de libertad.

Es importante trabajar con la expresión completa de ${\vec {v}}_{21}^{\,B}$, es decir, no imponer que la componente en ${\vec {\jmath }}_{1}$ es cero. Esto se debe a que hay que hacer las derivadas que se hacen a continuación antes de imponer la ligadura.

Función de Lagrange

Energía cinética

Modelando el triciclo como una barra de longitud $2a$ y masa $m$, su energía cinética es

$T={\dfrac {1}{2}}m|{\vec {v}}_{21}^{\,G}|^{2}+{\dfrac {1}{2}}I|{\vec {\omega }}_{21}|^{2}={\dfrac {1}{2}}m\,({\dot {x}}^{2}+{\dot {y}}^{2})+{\dfrac {1}{2}}I{\dot {\theta }}^{2}.\qquad (I=ma^{2}/3)$

El peso no afecta en este problema, pues el centro de masas del triciclo no cambia de altura. Por tanto podemos escoger como energía potencial

$U=0$

La función de Lagrange es

$L=T-U={\dfrac {1}{2}}m\,({\dot {x}}^{2}+{\dot {y}}^{2})+{\dfrac {1}{2}}I{\dot {\theta }}^{2}.$

Ecuaciones de Lagrange

Multiplicadores de Lagrange

Por cada vínculo hay que añadir un multiplicador de Lagrange. Tenemos

${\begin{array}{lcl}g_{1}={\dot {x}}\,\mathrm {sen} \,\theta -{\dot {y}}\cos \theta +a{\dot {\theta }}=0&\Longrightarrow &\mu _{1}.\\g_{2}={\dot {y}}+a{\dot {\theta }}\cos \theta =0&\Longrightarrow &\mu _{2}.\end{array}}$

Ecuaciones

Tenemos una ecuación de Lagrange por cada coordenada.

${\begin{array}{l}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {x}}}}\right)-{\dfrac {\partial L}{\partial x}}=Q_{x}^{ML}\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial l}{\partial {\dot {y}}}}\right)-{\dfrac {\partial l}{\partial y}}=Q_{y}^{ML}\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial l}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial l}{\partial \theta }}=Q_{\theta }^{ML}\end{array}}$

Los términos de la derecha son las contribuciones a las fuerzas generalizadas de los multiplicadores de Lagrange.

${\begin{array}{l}Q_{x}^{ML}=\mu _{1}\,{\dfrac {\partial g_{1}}{\partial {\dot {x}}}}+\mu _{2}\,{\dfrac {\partial g_{2}}{\partial {\dot {x}}}}=\mu _{1}\,\mathrm {sen} \,\theta ,\\Q_{y}^{ML}=\mu _{1}\,{\dfrac {\partial g_{1}}{\partial {\dot {y}}}}+\mu _{2}\,{\dfrac {\partial g_{2}}{\partial {\dot {y}}}}=-\mu _{1}\cos \theta +\mu _{2},\\Q_{\theta }^{ML}=\mu _{1}\,{\dfrac {\partial g_{1}}{\partial {\dot {\theta }}}}+\mu _{2}\,{\dfrac {\partial g_{2}}{\partial {\dot {\theta }}}}=\mu _{1}a+\mu _{2}a\cos \theta .\end{array}}$

Las derivadas parciales que introducen los multiplicadores de Lagrange se hacen respecto a la velocidad ${\dot {x}}$ porque los vínculos son cinemáticos.

Las ecuaciones resultantes son

${\begin{array}{lr}m{\ddot {x}}=\mu _{1}\,\mathrm {sen} \,\theta ,&(1)\\m{\ddot {y}}=-\mu _{1}\cos \theta +\mu _{2},&(2)\\I{\ddot {\theta }}=\mu _{1}a+\mu _{2}a\cos \theta .&(3)\end{array}}$

Tenemos 5 incógnitas $\{x,y,\theta .\mu _{1},\mu _{2}\}$. Las dos ecuaciones que faltan son los propios vínculos

${\begin{array}{lr}{\dot {x}}\,\mathrm {sen} \,\theta -{\dot {y}}\cos \theta +a{\dot {\theta }}=0,&(4)\\{\dot {y}}+a{\dot {\theta }}\cos \theta =0.&(5)\end{array}}$

Resolución usando el Principio de liberación

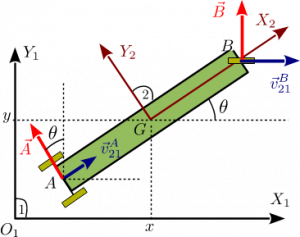
De nuevo vamos a trabajar con las tres coordenadas $\{x,y,\theta \},$ aunque sólo haya un grado de libertad. Por cada vínculo liberado hay que añadir una reacción vincular. El vínculo en $A$ implica que el punto $A$ no puede moverse dirección perpendicular al vector ${\overrightarrow {AB}}$. Por tanto, la fuerza víncular que hay que añadir, ${\vec {A}}$ es perpendicular a ${\overrightarrow {AB}}$. El vínculo en $B$ prohíbe que este punto se mueva en la dirección del eje $O_{1}Y_{1}$. Es decir, la fuerza vincular ${\vec {B}}$ debe ser paralela al eje $O_{1}Y_{1}$, en la dirección del movimiento prohibido. La figura de la derecha muestra las fuerzas vinculares. Tenemos

${\begin{array}{l}{\vec {A}}=-A\,\mathrm {sen} \,\theta \,{\vec {\imath }}_{1}+A\cos \theta \,{\vec {\jmath }}_{1},\\{\vec {B}}=B\,{\vec {\jmath }}_{1}.\end{array}}$

Ahora las ecuaciones de Lagrange incluyen la contribución de las fuerza vínculares ${\vec {A}}$ y ${\vec {B}}$. Tenemos

${\begin{array}{lcl}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {x}}}}\right)-{\dfrac {\partial L}{\partial x}}&=&Q_{x}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {y}}}}\right)-{\dfrac {\partial L}{\partial y}}&=&Q_{y}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial L}{\partial \theta }}&=&Q_{\theta }^{NC}.\end{array}}$

El lado izquierdo de estas ecuaciones es igual que el que hemos calculado antes. Lo que cambia son los lados derechos. Para $Q_{x}^{NC}$ tenemos

$Q_{x}^{NC}={\vec {A}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,A}}{\partial {\dot {x}}}}+{\vec {B}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {x}}}}={\vec {A}}\cdot ({\vec {\imath }}_{1})+{\vec {B}}\cdot ({\vec {\imath }}_{1})=-A\,\mathrm {sen} \,\theta .$

Para $Q_{y}^{NC}$ tenemos

$Q_{y}^{NC}={\vec {A}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,A}}{\partial {\dot {y}}}}+{\vec {B}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {y}}}}={\vec {A}}\cdot ({\vec {\jmath }}_{1})+{\vec {B}}\cdot ({\vec {\jmath }}_{1})=A\cos \theta +B.$

Para $Q_{\theta }^{NC}$ tenemos

$Q_{\theta }^{NC}={\vec {A}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,A}}{\partial {\dot {\theta }}}}+{\vec {B}}\cdot {\dfrac {\partial {\vec {v}}_{21}^{\,B}}{\partial {\dot {\theta }}}}={\vec {A}}\cdot (a\,\mathrm {sen} \,\theta \,{\vec {\imath }}_{1}-a\cos \theta {\vec {\jmath }}_{1})+{\vec {B}}\cdot (-a\,\mathrm {sen} \,\theta \,{\vec {\imath }}_{1}+a\cos \theta \,{\vec {\jmath }}_{1})=-aA+aB\cos \theta .$

Así pues, las ecuaciones de Lagrange quedan

${\begin{array}{lr}m{\ddot {x}}=-A\,\mathrm {sen} \,\theta ,&(6)\\m{\ddot {y}}=A\cos \theta +B,&(7)\\I{\ddot {\theta }}=-aA+aB\cos \theta .&(8)\end{array}}$

Las incógintas son $\{x,y,\theta ,A,B\}$. Las dos ecuaciones que faltan son los propios vínculos (y sus derivadas, si hacen falta)

${\begin{array}{lr}{\dot {x}}\,\mathrm {sen} \,\theta -{\dot {y}}\cos \theta +a{\dot {\theta }}=0,&(9)\\{\dot {y}}+a{\dot {\theta }}\cos \theta =0.&(10)\end{array}}$

Identificación de los multiplicadores de Lagrange

Podemos identificar el significado físico de los multiplicadores de Lagrange comparando las ecuaciones (1), (2), (3) con las ecuaciones (6), (7), (8). Vemos que

$\mu _{1}=-A,\qquad \mu _{2}=B.$

Es decir, los multiplicadores son componentes de fuerza. Eso se debe a que los vínculos provienen de restricciones a desplazamientos. Si el vínculo implica una restricción a una rotación, el multiplicador correspondiente será una componente de momento de fuerza. El signo de la componente depende de como definamos el vínculo. Así, si el vínculo en $A$ lo definimos como $-g_{1}=0$, saldría $\mu _{1}=A$.

Otra forma de identificar los multiplicadores es comparar las expresiones de la potencia transmitida al sólido por las fuerzas vinculares y los multiplicadores de Lagrange. La potencia vectorial sería

$P_{vec}={\vec {A}}\cdot {\vec {v}}_{21}^{\,A}+{\vec {B}}\cdot {\vec {v}}_{21}^{\,B}={\dot {x}}\,(-A\,\mathrm {sen} \,\theta )+{\dot {y}}\,(A\cos \theta +B)+{\dot {\theta }}\,(-Aa+Ba\cos \theta ).$

La potencia que transmiten las fuerzas generalizadas correspondientes a los multiplicadores de Lagrange es

$P_{ana}=Q_{x}^{ML}{\dot {x}}+Q_{y}^{ML}{\dot {y}}+Q_{\theta }^{ML}{\dot {\theta }}={\dot {x}}\,(\mu _{1}\,\mathrm {sen} \,\theta )+{\dot {y}}\,(\mu _{2}-\mu _{1}\cos \theta )+{\dot {\theta }}\,(\mu _{1}a+\mu _{2}a\cos \theta ).$

Comparando con la expresión de la potencia vectorial, los paréntesis que multiplican a las velocidades generalizadas deben ser iguales, de donde obtenemos de nuevo

$\mu _{1}=-A,\qquad \mu _{2}=B.$