Diferencia entre las páginas «Potencia y energía en una onda» y «Superposición de ondas»
(Página creada con «==Introducción== Una onda suele definirse en términos como una “transmisión de energía sin transmisión de materia”. Esta definición, aunque un tanto imprecisa y no lo bastante general (ya que no incluye, por ejemplo, a las ondas estacionarias), sí expresa un hecho cierto: una onda viajera transmite energía desde el punto en que se origina hasta el punto al que llega, actuando como mecanismo para la “acción a distancia”. Un cierto…») |
(Página creada con «==Introducción== Una de las propiedades de la ecuación de onda es que se trata de una ecuación ''lineal'', esto quiere decir que admite el principio de superposición. Esto significa que si <math>y_1</math> e <math>y_2</math> son las soluciones de la misma ecuación de onda <center><math>\frac{\partial^2y_1}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y_1}{\partial t^2}=0</math>{{qquad}}{{qquad}}<math>\frac{\partial^2y_2}{\partial x^2}-\frac{1}{v^2}\,\frac{\parti…») |
||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
Una | Una de las propiedades de la ecuación de onda es que se trata de una ecuación ''lineal'', esto quiere decir que admite el principio de superposición. Esto significa que si <math>y_1</math> e <math>y_2</math> son las soluciones de la misma ecuación de onda | ||
<center><math>\frac{\partial^2y_1}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y_1}{\partial t^2}=0</math>{{qquad}}{{qquad}}<math>\frac{\partial^2y_2}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y_2}{\partial t^2}=0</math></center> | |||
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución | |||
<center><math>y=y_1+y_2\,</math>{{tose}}<math>\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2y}{\partial t^2}=0</math></center> | |||
[[Imagen:viajera3.gif|left]][[Imagen:Estacio2.gif|450px|right]]Esto se aplica cualquiera que sean las ondas componentes. En el caso particular de pulsos de onda el resultado es que, aunque durante el periodo de coincidencia, la deformación de la cuerda puede adoptar formas extrañas, cuando se separan ambos pulsos continúan sin haber sido afectados en absoluto por la “colisión” con el otro. | |||
En el caso de ondas sinusoidales, el principio es el mismo. Sin embargo, dado que estas ondas se extienden (en teoría) indefinidamente en el espacio, la coincidencia se produce en todas partes todo el tiempo. Además, la forma de las ondas resultantes a menudo posee interpretación por sí misma. Por ello, interesa estudiar el resultado de la superposición de ondas armónicas, y no solo considerarlas como compuestas de sus ondas componentes (que a menudo son desconocidas o irrelevantes, pues lo que se observa es el resultado de la superposición. | |||
==Mismo sentido== | |||
===Misma frecuencia=== | |||
====Misma amplitud==== | |||
[[Imagen:Desfase1.gif|left]]Comenzamos suponiendo el caso más sencillo posible: dos ondas que se propagan por la misma cuerda en el mismo sentido, con la misma frecuencia y la misma amplitud, diferenciándose exclusivamente en su desfase. Podremos escribir estas dos señales como | |||
<center><math>y_1 = A_0\cos(\omega t - k x)\,</math>{{qquad}}{{qquad}} <math>y_2 = A_0\cos(\omega t - k x+\phi)\,</math></center> | |||
< | donde hemos tomado la primera señal como referencia y con desfase 0. A menudo, para hablar del desfase entre las dos ondas, en lugar del ángulo <math>\phi</math> se emplea la distancia <math>\Delta x</math> entre un máximo de una onda y el máximo de la otra, de forma que se habla de que están desfasadas “media longitud de onda” o “un cuarto de longitud de onda”, por ejemplo. La relación entre este desfase y el ángulo <math>\phi</math> es | ||
<center><math>\frac{\Delta x}{\lambda}=\frac{\phi}{2\pi}</math></center> | |||
Para estas dos señales, la superposición será | |||
= | <center><math>y = A_0\cos(\omega t - k x) + A_0\cos(\omega t - k x+\phi)\,</math></center> | ||
Aplicando aquí la relación trigonométrica que transforma sumas en productos | |||
<center><math>\cos(a)+\cos(b) = 2\cos\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right)</math></center> | |||
la superposición de ondas se nos convierte en | |||
y | <center><math>y = 2A_0\cos\left(\frac{\phi}{2}\right)\cos\left(\omega t - k x+\frac{\phi}{2}\right) = A(\phi)\cos\left(\omega t - k x+\phi'\right)</math></center> | ||
con | |||
<center><math>A(\phi) = 2A_0\cos\left(\frac{\phi}{2}\right)\qquad\qquad\phi'=\frac{\phi}{2}</math></center> | |||
Podemos interpretar este resultado de forma sencilla: la suma de dos ondas viajeras en el mismo sentido con la misma frecuencia y amplitud es una nueva onda viajera con un desfase que es la media de los desfases respectivos y cuya amplitud depende del desfase. | |||
Atendiendo al valor del desfase tenemos dos casos importantes: | |||
* '''Interferencia constructiva:''' Cuando el desfase entre las ondas es un múltiplo par de <math>\pi</math>, o en términos de la distancia entre máximos de las ondas, si están desfasados en un número entero de longitudes de onda | |||
<center><math>\phi = 2n\pi\,</math>{{tose}}<math>\Delta x = n\lambda\,</math></center> | |||
:en este caso las ondas son completamente coincidentes y la onda resultante es una en fase con ellas y con amplitud el doble de la cada una | |||
<center><math>\ | <center><math>A(0) = 2A_0\qquad\phi'(0)=0</math></center> | ||
:Se dice entonces que estas ondas ''están en fase'' y poseen ''interferencia constructiva''. | |||
:Nótese que al ser la amplitud el doble, la energía de la onda resultante es el cuádruple de la de las ondas componentes y lo mismo ocurre con la potencia, esto es, que la energía de la suma no es igual a la suma de las energías. | |||
* '''Interferencia destructiva:''' Cuando el desfase entre las ondas es un múltiplo impar de <math>\pi</math>, o en términos de la longitud, cuando se diferencian en un múltiplo semientero de la longitud de onda (media longitud de onda, longitud y media, dos longitudes y media,…) | |||
<center><math>\phi = (2n+1)\pi\,</math>{{tose}}<math>\Delta x = n\lambda\,</math></center> | |||
:Si las ondas se encuentran en esta situación (denominada ''contrafase'' u ''oposición de fase'') las ondas son exactamente iguales, pero de signo contrario, con lo que se cancelan mutuamente y el resultado es una onda nula (de ahí lo de ''interferencia destructiva''). | |||
A | <center><math>A(\pi) = 0 \qquad \phi'=\frac{\pi}{2}</math></center> | ||
:Para esta interferencia la energía almacenada es naturalmente nula y lo mismo ocurre con la potencia. De nuevo comprobamos que la energía de la suma no es la suma de las energías. | |||
* Otras interferencias: cuando las ondas se encuentran en una situación intermedia entre estar en fase o en oposición de fase, el resultado es una onda cuya amplitud es intermedia entre 0 y <math>2A_0</math>. En particular, existe un desfase para el cual la suma de las ondas tiene exactamente la misma amplitud que cada una de los sumandos. | |||
<center> | |||
{| class="bordeado" | |||
|- | |||
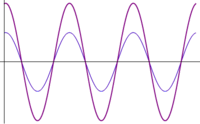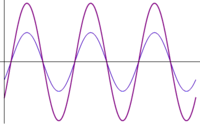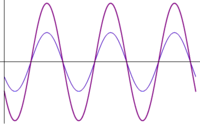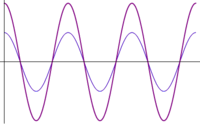
| [[Imagen:desfase-0.gif|200px]] | |||
| [[Imagen:desfase-pi.gif|200px]] | |||
| [[Imagen:desfase-pi2.gif|200px]] | |||
| [[Imagen:desfase-pi3.gif|200px]] | |||
|- | |||
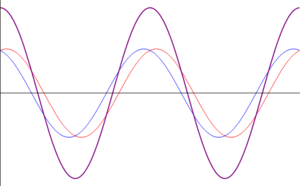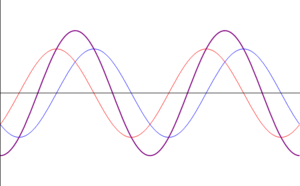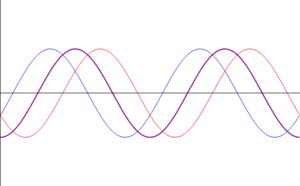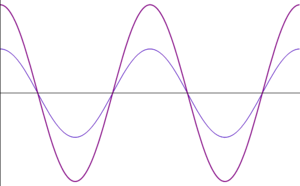
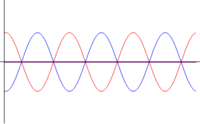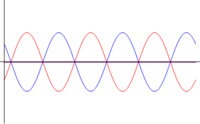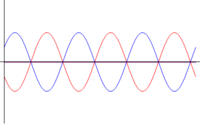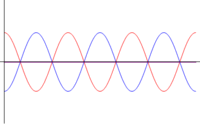
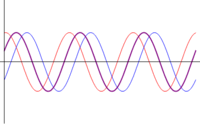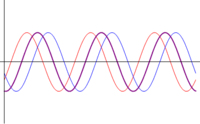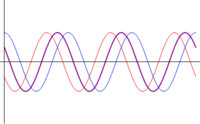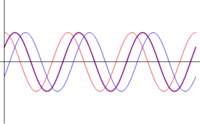
| <math>\phi=0\,</math> | |||
| <math>\phi=\pi\,</math> | |||
| <math>\phi=\pi/2\,</math> | |||
| <math>\phi=2\pi/3\,</math> | |||
|} | |||
</center> | |||
====Diferente amplitud==== | |||
Supongamos ahora que tenemos dos ondas de la misma frecuencia propagándose en el mismo sentido, pero de diferente amplitud y fase: | |||
<center><math>\ | <center><math>y_1 = A_1\cos(\omega t - k x)\,</math>{{qquad}}{{qquad}}<math>y_2 = A_2\cos(\omega t - k x + \phi)\,</math></center> | ||
y la | En este caso, el uso de relaciones trigonométricas no es tan simple como en el caso anterior, así que primero consideraremos dos casos sencillos y posteriormente daremos la solución general, con ayuda del cálculo fasorial. | ||
* '''Interferencia constructiva:''' Si el desfase es nulo, las dos ondas están en fase y el resultado es una onda con amplitud la suma de ambas | |||
<center><math>\phi=0\,</math>{{tose}}<math>y=y_1 +y_2= (A_1+A_2)\cos(\omega t - k x)\,</math></center> | |||
<center><math> | |||
= | * '''Interferencia destructiva:''' Si las ondas se encuentran en contrafase (<math>\phi=\pi</math>), no se produce la anulación completa, por ser una de las ondas de mayor amplitud que la otra. La suma de ambas señales da | ||
<center><math>\phi=\pi\,</math>{{tose}}<math>y=y_1 +y_2= (A_1-A_2)\cos(\omega t - k x)\,</math></center> | |||
:Si tenemos en cuenta que la amplitud siempre la consideramos positiva, esta superposición debe escribirse de forma correcta como | |||
<center><math>\phi=\pi\,</math>{{tose}}<math>y=y_1 +y_2= |A_1-A_2|\cos(\omega t - k x+\phi')\,</math></center> | |||
:con | |||
<center><math>\ | <center><math>\phi'=\begin{cases}0 & A_1>A_2\\ \pi & A_1 < A_2\end{cases}</math></center> | ||
[[Imagen:sumafasores.gif|left]] | |||
En el caso general de amplitudes diferentes y fase arbitraria, podemos hacer uso del cálculo fasorial. Cada una de las señales se puede poner en la forma | |||
<center><math>\begin{matrix}y_1 & = & A_1\cos(\omega t-k x) = \mathrm{Re}\left(A_1 \mathrm{e}^{\mathrm{j}(\omega t - k x)}\right) = \mathrm{Re}\left(\tilde{y}_1 \mathrm{e}^{\mathrm{j}(\omega t-kx))}\right)\\ y_2 & = & A_2\cos(\omega t-k x+\phi) = \mathrm{Re}\left(A_2 \mathrm{e}^{\mathrm{j}(\omega t - k x+\phi)}\right) = \mathrm{Re}\left(\tilde{y}_2 \mathrm{e}^{\mathrm{j}(\omega t-kx)}\right)\end{matrix}</math></center> | |||
siendo los fasores de cada una | |||
y | <center><math>\tilde{y}_1 = A_1\,</math>{{qquad}}{{qquad}}<math>\tilde{y}_2=A_2\mathrm{e}^{\mathrm{j}\phi}\,</math></center> | ||
[[Imagen:sumafasores.png|300px|right]] | |||
Cuando sumemos estas dos ondas, el resultado será una nueva onda, con fasor | |||
<center><math>\ | <center><math>\tilde{y} = \tilde{y}_1+\tilde{y}_2=A_1+A_2\mathrm{e}^{\mathrm{j}\phi}=</math></center> | ||
Esta suma de números complejos la posemos escribir como un solo fasor que combina la amplitud y el desfase de la onda resultante | |||
<center><math> | <center><math>\tilde{y} = A_1+A_2\mathrm{e}^{\mathrm{j}\phi}=A\mathrm{e}^{\mathrm{j}\phi'}</math></center> | ||
La amplitud de las oscilaciones será el módulo del número complejo | |||
<center><math> | <center><math>A = \sqrt{\tilde{y}\tilde{y}^*} = \sqrt{(A_1+A_2\mathrm{e}^{\mathrm{j}\phi})(A_1+A_2\mathrm{e}^{-\mathrm{j}\phi})}=\sqrt{A_1^2+A_2^2+A_1A_2(\mathrm{e}^{\mathrm{j}\phi}+\mathrm{e}^{-\mathrm{j}\phi})}</math></center> | ||
y, aplicando la fórmula de Euler obtenemos finalmente | |||
<center><math>A = \sqrt{A_1^2+A_2^2+2A_1A_2\cos(\phi)}</math></center> | |||
Este módulo es el de la suma vectorial de los dos fasores, considerados como vectores en el plano complejo. | |||
Podemos comprobar que los dos casos anteriores están contenidos en este resultado: | |||
* Si <math>\phi=0\,</math>, <math>\cos\phi=1\,</math> y la amplitud se reduce a | |||
<center><math> | <center><math>A = \sqrt{A_1^2+A_2^2+2A_1A_2}=\sqrt{(A_1+A_2)^2}=A_1+A_2</math></center> | ||
y | * Si <math>\phi=\pi\,</math>, <math>\cos\phi=-1\,</math> y queda la amplitud | ||
<center><math>\ | <center><math>A = \sqrt{A_1^2+A_2^2-2A_1A_2}=\sqrt{(A_1-A_2)^2}=|A_1-A_2|</math></center> | ||
También podemos reobtener el caso de que ambas señales tengan la misma amplitud, para cualquier fase. Si <math>A_1=A_2=A_0</math> | |||
<center><math>\ | <center><math>A = \sqrt{A_0^2+A_0^2+2A_0^2\cos(\phi)}=2A_0\sqrt{\frac{1+\cos(\phi)}{2}}=2A_0\cos\left(\frac{\phi}{2}\right)</math></center> | ||
Además de la amplitud, obtenemos el desfase de la onda resultante como el argumento del fasor | |||
<center> | |||
<math>\phi'=\mathrm{arctg}\left(\frac{\mathrm{Im}(\tilde{y})}{\mathrm{Re}(\tilde{y})}\right)=\mathrm{arctg}\left(\frac{A_2\,\mathrm{sen}\,(\phi)}{A_1+A_2\cos(\phi)}\right)</math></center> | |||
<center><math>\ | <center> | ||
{| class="bordeado" | |||
|- | |||
| [[Imagen:desfase-0-05.gif|200px]] | |||
| [[Imagen:desfase-pi-05.gif|200px]] | |||
| [[Imagen:desfase-2pi3-05.gif|200px]] | |||
|- | |||
| <math>\phi=0\ A_1=2A_2\,</math> | |||
| <math>\phi=\pi\ A_1=2A_2\,</math> | |||
| <math>\phi=2\pi/3\ A_1=2A_2\,</math> | |||
|} | |||
</center> | |||
En cuanto a la energía de la onda resultante, aplicando la fórmula para la energía contenida en una onda nos queda | |||
=== | <center><math>E = \frac{\mu \omega^2\lambda A^2}{2}= \frac{\mu \omega^2\lambda}{2}(A_1^2+A_2^2+2A_1A_2\cos(\phi)) = E_1+E_2+\mu\omega^2\lambda A_1A_2\cos(\phi)</math></center> | ||
que se lee como que la energía de la suma es igual a la suma de las energías, más un término que depende de las amplitudes y del desfase, y que puede ser tanto positivo (en interferencia constructiva) como negativo (en interferencia destructiva). | |||
===Frecuencias próximas (batidos)=== | |||
{{ac|Interferencia de ondas de frecuencias próximas}} | |||
==Sentido opuesto== | |||
===Misma amplitud=== | |||
Vamos a examinar ahora el caso de que tengamos dos ondas viajeras de la misma frecuencia y amplitud y propagándose en sentidos opuestos: | |||
<center><math>y_1 = A\cos(\omega t - k x)\,</math>{{qquad}}{{qquad}}<math>y_2 = A\cos(\omega t+kx)\,</math></center> | |||
En este caso no es necesario introducir la constante <math>\phi\,</math> porque, para ondas que van en sentidos opuestos el concepto de desfase no tiene mucho sentido. Se puede incluir esta constante, pero los resultados no se diferencian en lo esencial de lo que se obtiene sin ella. | |||
[[Imagen:Estacio2.gif|300px|right]] | |||
La superposición de estas dos señales se puede transformar aplicando relaciones trigonométricas | |||
<center><math> | <center><math>y=y_1 + y_2 = A\cos(\omega t - kx)+A\cos(\omega t + k x)=2A\cos(\omega t)\cos(kx)\,</math></center> | ||
Esta es la ecuación de una [[Solución de onda estacionaria|onda estacionaria]], que se puede escribir en la forma | |||
<center><math>y = | <center><math>y = A(x)\cos(\omega t)\,</math>{{qquad}}{{qquad}}<math>A(x) = 2A\cos(k x)\,</math></center> | ||
la | Lo que nos dice esta ecuación es que aunque tenemos la superposición de dos ondas viajeras, la suma es una onda en que todos los puntos oscilan en fase, con una amplitud dependiente de su posición. En los puntos en que resulta una amplitud <math>A(x)</math> negativa, debe entenderse que la amplitud es el valor absoluto de esta cantidad y que los puntos correspondientes están en ''oposición de fase'' (esto es, tienen una constante de fase igual a π). | ||
[[Imagen:Estacio3.gif|300px|right]] | |||
La | ;Nodos: La amplitud varía como un coseno, lo cual implica que existen puntos para los cuales la amplitud de oscilación es nula. Estos puntos se denominan '''nodos'''. La posición de estos nodos la da la condición | ||
<center><math>\frac{\ | <center><math>A(x_n) = 2A\cos(kx_n) = 0\,</math>{{tose}} <math>kx_n = \frac{\pi}{2}+n\pi</math>{{tose}} <math>\Delta x = x_{n+1}-x_n = \frac{\pi}{k}=\frac{\lambda}{2}</math></center> | ||
:La distancia entre nodos consecutivos es media longitud de onda | |||
;Vientres: Los puntos en que la amplitud de oscilación es máxima se denominan ''vientres''. Los vientres se encuentran en los puntos medios entre nodos, y por tanto la distancia entre vientres consecutivos es también media longitud de onda, y la distancia de un vientre al nodo más próximo es <math>\lambda/4</math>. | |||
===Diferente amplitud=== | |||
Si las dos ondas no son de la misma amplitud, | |||
== | <center><math>y_1 = A_1\cos(\omega t - kx)\,</math>{{qquad}}{{qquad}}<math>y_2=A_2\cos(\omega t + kx)\,</math></center> | ||
la superposición se compone de una parte estacionaria y de una parte viajera. | |||
Para | Supongamos que <math>A_1 > A_2</math>. Para la primera onda podemos escribir trivialmente | ||
<center><math>y_1 = A_1\cos(\omega t - k x) = (A_1-A_2)\cos(\omega t - k x) + A_2\cos(\omega t - k x)\,</math></center> | |||
Sumando con la segunda | |||
<center><math>y = y_1+y_2 = (A_1-A_2)\cos(\omega t - k x) + 2A_2\cos(\omega t)\cos(k x)\,</math></center> | |||
Comparando las figuras siguientes que el primer caso (dos ondas viajeras) tiene la misma suma que la segunda (una onda viajera -naranja-y una estacionaria -verde-) | |||
: | <center> | ||
[[Imagen:Viajerasdesiguales01.gif]]</center> | |||
[[Categoría:Movimiento ondulatorio]] | [[Categoría:Movimiento ondulatorio]] | ||
Revisión actual - 17:15 11 dic 2023
Introducción
Una de las propiedades de la ecuación de onda es que se trata de una ecuación lineal, esto quiere decir que admite el principio de superposición. Esto significa que si e son las soluciones de la misma ecuación de onda
(esto es, ambas representan posibles ondas que se pueden propagar por la misma cuerda), entonces su suma también es solución

Esto se aplica cualquiera que sean las ondas componentes. En el caso particular de pulsos de onda el resultado es que, aunque durante el periodo de coincidencia, la deformación de la cuerda puede adoptar formas extrañas, cuando se separan ambos pulsos continúan sin haber sido afectados en absoluto por la “colisión” con el otro.
En el caso de ondas sinusoidales, el principio es el mismo. Sin embargo, dado que estas ondas se extienden (en teoría) indefinidamente en el espacio, la coincidencia se produce en todas partes todo el tiempo. Además, la forma de las ondas resultantes a menudo posee interpretación por sí misma. Por ello, interesa estudiar el resultado de la superposición de ondas armónicas, y no solo considerarlas como compuestas de sus ondas componentes (que a menudo son desconocidas o irrelevantes, pues lo que se observa es el resultado de la superposición.
Mismo sentido
Misma frecuencia
Misma amplitud
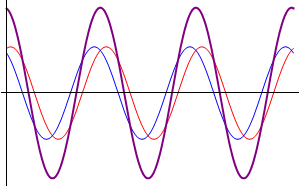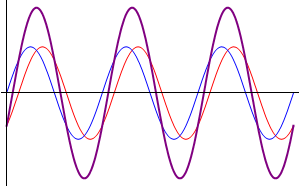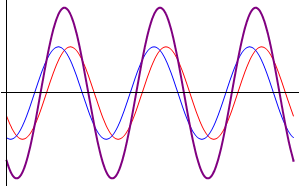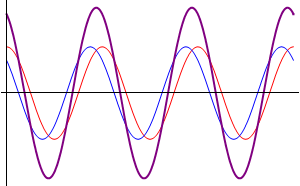
Comenzamos suponiendo el caso más sencillo posible: dos ondas que se propagan por la misma cuerda en el mismo sentido, con la misma frecuencia y la misma amplitud, diferenciándose exclusivamente en su desfase. Podremos escribir estas dos señales como
donde hemos tomado la primera señal como referencia y con desfase 0. A menudo, para hablar del desfase entre las dos ondas, en lugar del ángulo se emplea la distancia entre un máximo de una onda y el máximo de la otra, de forma que se habla de que están desfasadas “media longitud de onda” o “un cuarto de longitud de onda”, por ejemplo. La relación entre este desfase y el ángulo es
Para estas dos señales, la superposición será
Aplicando aquí la relación trigonométrica que transforma sumas en productos
la superposición de ondas se nos convierte en
con
Podemos interpretar este resultado de forma sencilla: la suma de dos ondas viajeras en el mismo sentido con la misma frecuencia y amplitud es una nueva onda viajera con un desfase que es la media de los desfases respectivos y cuya amplitud depende del desfase.
Atendiendo al valor del desfase tenemos dos casos importantes:
- Interferencia constructiva: Cuando el desfase entre las ondas es un múltiplo par de , o en términos de la distancia entre máximos de las ondas, si están desfasados en un número entero de longitudes de onda
- en este caso las ondas son completamente coincidentes y la onda resultante es una en fase con ellas y con amplitud el doble de la cada una
- Se dice entonces que estas ondas están en fase y poseen interferencia constructiva.
- Nótese que al ser la amplitud el doble, la energía de la onda resultante es el cuádruple de la de las ondas componentes y lo mismo ocurre con la potencia, esto es, que la energía de la suma no es igual a la suma de las energías.
- Interferencia destructiva: Cuando el desfase entre las ondas es un múltiplo impar de , o en términos de la longitud, cuando se diferencian en un múltiplo semientero de la longitud de onda (media longitud de onda, longitud y media, dos longitudes y media,…)
- Si las ondas se encuentran en esta situación (denominada contrafase u oposición de fase) las ondas son exactamente iguales, pero de signo contrario, con lo que se cancelan mutuamente y el resultado es una onda nula (de ahí lo de interferencia destructiva).
- Para esta interferencia la energía almacenada es naturalmente nula y lo mismo ocurre con la potencia. De nuevo comprobamos que la energía de la suma no es la suma de las energías.
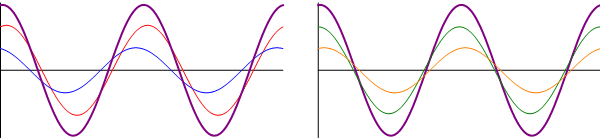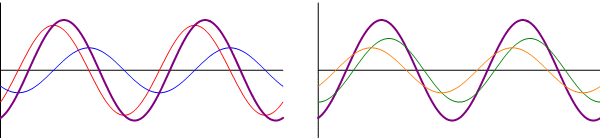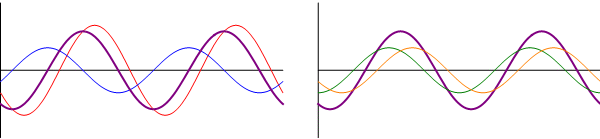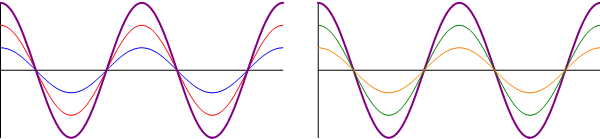
- Otras interferencias: cuando las ondas se encuentran en una situación intermedia entre estar en fase o en oposición de fase, el resultado es una onda cuya amplitud es intermedia entre 0 y . En particular, existe un desfase para el cual la suma de las ondas tiene exactamente la misma amplitud que cada una de los sumandos.
|
|

|
|
Diferente amplitud
Supongamos ahora que tenemos dos ondas de la misma frecuencia propagándose en el mismo sentido, pero de diferente amplitud y fase:
En este caso, el uso de relaciones trigonométricas no es tan simple como en el caso anterior, así que primero consideraremos dos casos sencillos y posteriormente daremos la solución general, con ayuda del cálculo fasorial.
- Interferencia constructiva: Si el desfase es nulo, las dos ondas están en fase y el resultado es una onda con amplitud la suma de ambas
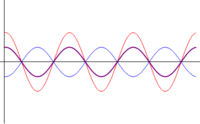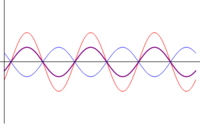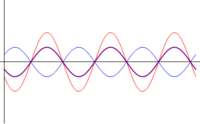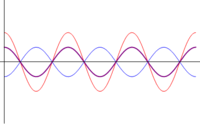
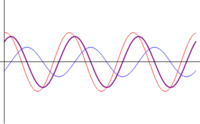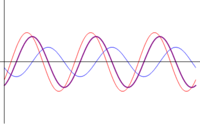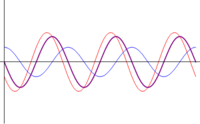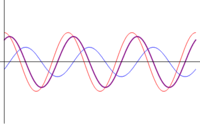
- Interferencia destructiva: Si las ondas se encuentran en contrafase (), no se produce la anulación completa, por ser una de las ondas de mayor amplitud que la otra. La suma de ambas señales da
- Si tenemos en cuenta que la amplitud siempre la consideramos positiva, esta superposición debe escribirse de forma correcta como
- con
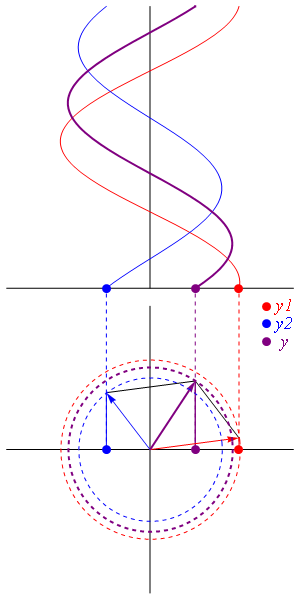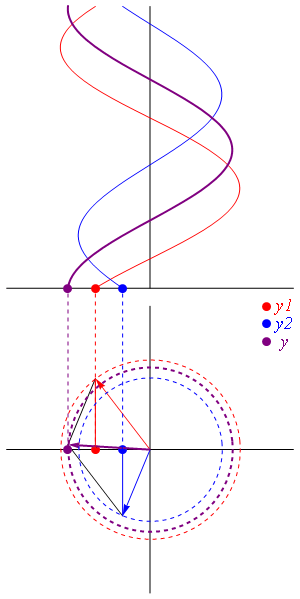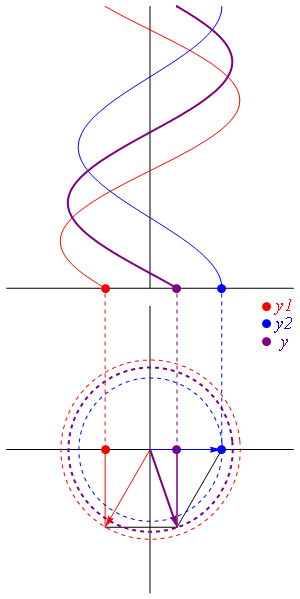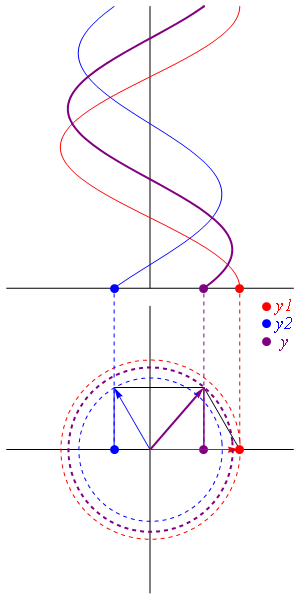
En el caso general de amplitudes diferentes y fase arbitraria, podemos hacer uso del cálculo fasorial. Cada una de las señales se puede poner en la forma
siendo los fasores de cada una
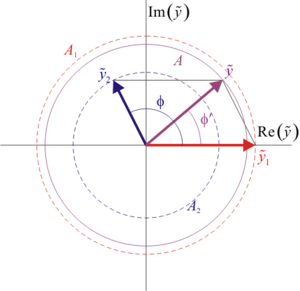
Cuando sumemos estas dos ondas, el resultado será una nueva onda, con fasor
Esta suma de números complejos la posemos escribir como un solo fasor que combina la amplitud y el desfase de la onda resultante
La amplitud de las oscilaciones será el módulo del número complejo
y, aplicando la fórmula de Euler obtenemos finalmente
Este módulo es el de la suma vectorial de los dos fasores, considerados como vectores en el plano complejo.
Podemos comprobar que los dos casos anteriores están contenidos en este resultado:
- Si , y la amplitud se reduce a
- Si , y queda la amplitud
También podemos reobtener el caso de que ambas señales tengan la misma amplitud, para cualquier fase. Si
Además de la amplitud, obtenemos el desfase de la onda resultante como el argumento del fasor
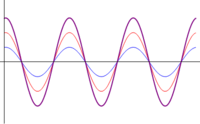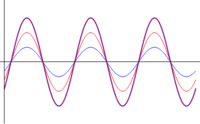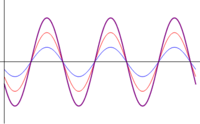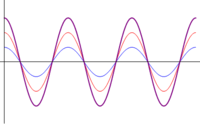
|
|
|
En cuanto a la energía de la onda resultante, aplicando la fórmula para la energía contenida en una onda nos queda
que se lee como que la energía de la suma es igual a la suma de las energías, más un término que depende de las amplitudes y del desfase, y que puede ser tanto positivo (en interferencia constructiva) como negativo (en interferencia destructiva).
Frecuencias próximas (batidos)
Sentido opuesto
Misma amplitud
Vamos a examinar ahora el caso de que tengamos dos ondas viajeras de la misma frecuencia y amplitud y propagándose en sentidos opuestos:
En este caso no es necesario introducir la constante porque, para ondas que van en sentidos opuestos el concepto de desfase no tiene mucho sentido. Se puede incluir esta constante, pero los resultados no se diferencian en lo esencial de lo que se obtiene sin ella.

La superposición de estas dos señales se puede transformar aplicando relaciones trigonométricas
Esta es la ecuación de una onda estacionaria, que se puede escribir en la forma
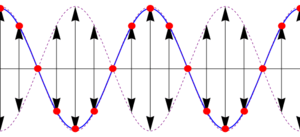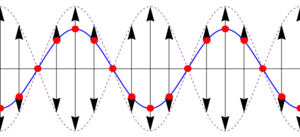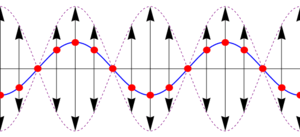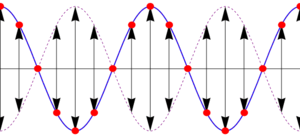
Lo que nos dice esta ecuación es que aunque tenemos la superposición de dos ondas viajeras, la suma es una onda en que todos los puntos oscilan en fase, con una amplitud dependiente de su posición. En los puntos en que resulta una amplitud negativa, debe entenderse que la amplitud es el valor absoluto de esta cantidad y que los puntos correspondientes están en oposición de fase (esto es, tienen una constante de fase igual a π).
- Nodos
- La amplitud varía como un coseno, lo cual implica que existen puntos para los cuales la amplitud de oscilación es nula. Estos puntos se denominan nodos. La posición de estos nodos la da la condición
- La distancia entre nodos consecutivos es media longitud de onda
- Vientres
- Los puntos en que la amplitud de oscilación es máxima se denominan vientres. Los vientres se encuentran en los puntos medios entre nodos, y por tanto la distancia entre vientres consecutivos es también media longitud de onda, y la distancia de un vientre al nodo más próximo es .
Diferente amplitud
Si las dos ondas no son de la misma amplitud,
la superposición se compone de una parte estacionaria y de una parte viajera.
Supongamos que . Para la primera onda podemos escribir trivialmente
Sumando con la segunda
Comparando las figuras siguientes que el primer caso (dos ondas viajeras) tiene la misma suma que la segunda (una onda viajera -naranja-y una estacionaria -verde-)