Diferencia entre las páginas «Archivo:F1GIERM-2019-masas-cuerda-muelle.png» y «Masas unidas por una cuerda con muelle, Octubre 2019 (G.I.E.R.M.)»
Sin resumen de edición |
(Página creada con «= Enunciado = right|300px La masa <math>m_1</math> de la figura está engarzada en un hilo horizontal sin rozamiento. La masa <math>m_2</math> desliza sobre una superficie horizontal también lisa. La distancia entre las líneas horizontales es <math>h=3d_0</math>. Las dos masas están unidas por una cuerda ideal sin masa de longitud <math>L=5d_0</math>. La cuerda está siempre tensa. La gravedad actúa como se indica en…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[File:F1GIERM-2019-masas-cuerda-muelle.png|right|300px]] | |||
La masa <math>m_1</math> de la figura está engarzada en un hilo horizontal sin rozamiento. | |||
La masa <math>m_2</math> desliza sobre una superficie horizontal también lisa. La distancia | |||
entre las líneas horizontales es <math>h=3d_0</math>. Las dos | |||
masas están unidas por una cuerda ideal sin masa de longitud <math>L=5d_0</math>. La cuerda | |||
está siempre tensa. La gravedad | |||
actúa como se indica en la figura. La masa <math>m_2</math> está a su vez unida a un muelle | |||
de longitud natural nula y constate elástica <math>k</math>. El otro extremo del muelle está | |||
anclado en el punto <math>O</math>. La masa <math>m_1</math> está sometida a la acción de una fuerza | |||
horizontal <math>\vec{F} = F\,\vec{\imath}</math>. | |||
#Dibuja el diagrama de fuerzas que actúa sobre cada partícula. | |||
#Calcula el vector de posición de la partícula 1. | |||
#En situación de equilibrio estático, encuentra la tensión de la cuerda y la fuerza que la superficie horizontal ejerce sobre la masa <math>m_2</math>. | |||
#Supongamos ahora que el contacto entre la masa <math>m_2</math> y la superficie horizontal es rugoso con un coeficiente de rozamiento estático <math>\mu=2</math>. Además, la masa <math>m_2</math> se ajusta para que <math>m_2g=F</math>. ¿Qué condición debe cumplir <math>F</math> para que el punto <math>A_2</math> de coordenada <math>x_2=d_0</math> sea un punto de equilibrio estático? | |||
= Solución = | |||
== Diagrama de fuerzas == | |||
[[File:F1GIERM-2019-masas-cuerda-muelle-fuerzas.png|right|300px]] | |||
La figura de la derecha muestra las fuerzas que actúan sobre cada partícula. Vamos a expresar estas fuerzas en el sistema de ejes de la figura. Para la partícula 1 tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{F} = F\,\vec{\imath},\\ | |||
\vec{P}_1 = -m_1g\,\vec{\jmath}\\ | |||
\vec{N}_1 = N_1\,\vec{\jmath},\\ | |||
\vec{T}_1 = -T\cos\beta\,\vec{\imath} - T\,\mathrm{sen}\,\beta\,\vec{\jmath}. | |||
\end{array} | |||
</math> | |||
</center> | |||
Para la partícula 2 tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{T}_2 = -\vec{T}_1 = T\cos\beta\,\vec{\imath} + T\,\mathrm{sen}\,\beta\,\vec{\jmath},\\ | |||
\vec{F}_k = -kx_2\,\vec{\imath},\\ | |||
\vec{P}_2 = -m_2g\,\vec{\jmath}\\ | |||
\vec{N}_2 = N_2\,\vec{\jmath}.\\ | |||
\end{array} | |||
</math> | |||
</center> | |||
El ángulo <math>\beta</math> es | |||
<center> | |||
<math> | |||
\mathrm{sen}\,\beta = \dfrac{h}{L} = \dfrac{3}{5} | |||
\Longrightarrow | |||
\cos\beta = \sqrt{1-\mathrm{sen}^2\,\beta} = \dfrac{4}{5}. | |||
</math> | |||
</center> | |||
== Vector de posición de la partícula 1 == | |||
Observando el dibujo vemos que | |||
<center> | |||
<math> | |||
\overrightarrow{OP}_1 = \overrightarrow{OP}_2 + \overrightarrow{P_1P}_2 = (x_2 + 4d_0)\,\vec{\imath} + 3d_0\,\vec{\jmath}. | |||
</math> | |||
</center> | |||
== Valor de las fuerzas en equilibrio estático == | |||
Para que haya equilibrio estático la suma de fuerzas sobre cada masa debe ser nula. Para la partícula 1 tenemos | |||
<center> | |||
<math> | |||
\vec{F} + \vec{P}_1 + \vec{N}_1 + \vec{T}_1 = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
X) & \to & F - \dfrac{4}{5}T = 0, & (1)\\ | |||
Y) & \to & -m_1g + N_1 - \dfrac{3}{5}T = 0. & (2) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Para la partícula 2 tenemos | |||
<center> | |||
<math> | |||
\vec{F}_k + \vec{P}_2 + \vec{N}_2 + \vec{T}_2 = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
X) & \to & -kx_2 + \dfrac{4}{5}T = 0, & (3)\\ | |||
Y) & \to & -m_2g + N_2 + \dfrac{3}{5}T = 0. & (4) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Resolviendo obtenemos | |||
<center> | |||
<math> | |||
x_2 = \dfrac{F}{k}\,\qquad T = \dfrac{5}{4}F, \qquad N_1 = m_1g + \dfrac{3}{4}F,\qquad N_2 = m_2g - \dfrac{3}{4}F. | |||
</math> | |||
</center> | |||
== Análisis con rozamiento == | |||
[[File:F1GIERM-2019-masas-cuerda-muelle-fuerzas-rozamiento.png|right|300px]] | |||
Al incluir el rozamiento debemos añadir una fuerza actuando sobre la partícula 2. La figura de la derecha muestra el diagrama de fuerzas para esta situación. Las fuerzas sobre la partícula 1 tienen las mismas expresiones | |||
que antes | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{F} = F\,\vec{\imath},\\ | |||
\vec{P}_1 = -m_1g\,\vec{\jmath}\\ | |||
\vec{N}_1 = N_1\,\vec{\jmath},\\ | |||
\vec{T}_1 = -T\cos\beta\,\vec{\imath} - T\,\mathrm{sen}\,\beta\,\vec{\jmath}. | |||
\end{array} | |||
</math> | |||
</center> | |||
Para la partícula 2 | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{T}_2 = -\vec{T}_1 = T\cos\beta\,\vec{\imath} + T\,\mathrm{sen}\,\beta\,\vec{\jmath},\\ | |||
\vec{F}_k = -kx_2\,\vec{\imath},\\ | |||
\vec{P}_2 = -m_2g\,\vec{\jmath}\\ | |||
\vec{N}_2 = N_2\,\vec{\jmath},\\ | |||
\vec{F}_R = f\,\vec{\imath}. | |||
\end{array} | |||
</math> | |||
</center> | |||
Aplicamos de nuevo la condición de equilibrio estático a cada partícula. La diferencia es que tenemos una incógnita mas, la magnitud de la fuerza de rozamiento. Pero ahora la posición de la partícula 2 es un dato. <math>x_2 = d_0</math>Para la partícula 1 tenemos | |||
<center> | |||
<math> | |||
\vec{F} + \vec{P}_1 + \vec{N}_1 + \vec{T}_1 = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
X) & \to & F - \dfrac{4}{5}T = 0, & (5)\\ | |||
Y) & \to & -m_1g + N_1 - \dfrac{3}{5}T = 0. & (6) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Para la partícula 2 tenemos | |||
<center> | |||
<math> | |||
\vec{F}_k + \vec{P}_2 + \vec{N}_2 + \vec{T}_2 + \vec{F}_R = \vec{0} | |||
\Longrightarrow | |||
\left\{ | |||
\begin{array}{lclr} | |||
X) & \to & -kd_0 + \dfrac{4}{5}T + f= 0, & (7)\\ | |||
Y) & \to & -m_2g + N_2 + \dfrac{3}{5}T = 0. & (8) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Resolviendo obtenemos | |||
<center> | |||
<math> | |||
f = kd_0-F, \qquad N2 = \dfrac{4m_2g-3F}{4}, \qquad N_1 = \dfrac{4m_1g+3F}{4}, \qquad T = \dfrac{5}{4}F. | |||
</math> | |||
</center> | |||
Utilizando la condición dada por el enunciado <math>m_2g = F</math>, obtenemos para las fuerzas normal y de rozamiento sobre la partícula 2 | |||
<center> | |||
<math> | |||
\vec{N}_2 = \dfrac{1}{4}F\,\vec{\jmath}, \qquad \vec{F}_R = (kd_0 - F)\,\vec{\imath}. | |||
</math> | |||
</center> | |||
La condición de no deslizamiento es | |||
<center> | |||
<math> | |||
|\vec{F}_R| \leq \mu|\vec{N}| | |||
\Longrightarrow | |||
|kd_0-F| \leq \mu F/4. | |||
</math> | |||
</center> | |||
Si utilizamos el valor del enunciado <math>\mu=2</math> la condición queda | |||
<center> | |||
<math> | |||
|kd_0-F| \leq F/2. | |||
</math> | |||
</center> | |||
Podemos considerar dos situaciones aquí. Por un lado | |||
<center> | |||
<math> | |||
kd_0>F \to |kd_0-F| = kd_0-F \to kd_0-F < F/2 \to kd_0 < 3F/2 \to F > 2kd_0/3. | |||
</math> | |||
</center> | |||
Por el otro | |||
<center> | |||
<math> | |||
kd_0<F \to |kd_0-F| = -kd_0+F \to -kd_0+F < F/2 \to F/2 < kd_0 \to F < 2kd_0. | |||
</math> | |||
</center> | |||
Por tanto, la condición que debe cumplir la fuerza para que no haya deslizamiento es | |||
<center> | |||
<math> | |||
F\in \left[\dfrac{2}{3}kd_0, 2kd_0\right]. | |||
</math> | |||
</center> | |||
[[Categoría:Dinámica del punto material|1]] | |||
[[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]] | |||
[[Categoría:Física I (G.I.E.R.M.)]] | |||
Revisión actual - 14:41 31 oct 2023
Enunciado
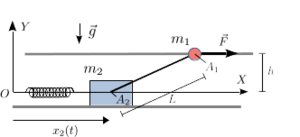
La masa de la figura está engarzada en un hilo horizontal sin rozamiento. La masa desliza sobre una superficie horizontal también lisa. La distancia entre las líneas horizontales es . Las dos masas están unidas por una cuerda ideal sin masa de longitud . La cuerda está siempre tensa. La gravedad actúa como se indica en la figura. La masa está a su vez unida a un muelle de longitud natural nula y constate elástica . El otro extremo del muelle está anclado en el punto . La masa está sometida a la acción de una fuerza horizontal .
- Dibuja el diagrama de fuerzas que actúa sobre cada partícula.
- Calcula el vector de posición de la partícula 1.
- En situación de equilibrio estático, encuentra la tensión de la cuerda y la fuerza que la superficie horizontal ejerce sobre la masa .
- Supongamos ahora que el contacto entre la masa y la superficie horizontal es rugoso con un coeficiente de rozamiento estático . Además, la masa se ajusta para que . ¿Qué condición debe cumplir para que el punto de coordenada sea un punto de equilibrio estático?
Solución
Diagrama de fuerzas
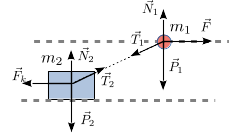
La figura de la derecha muestra las fuerzas que actúan sobre cada partícula. Vamos a expresar estas fuerzas en el sistema de ejes de la figura. Para la partícula 1 tenemos
Para la partícula 2 tenemos
El ángulo es
Vector de posición de la partícula 1
Observando el dibujo vemos que
Valor de las fuerzas en equilibrio estático
Para que haya equilibrio estático la suma de fuerzas sobre cada masa debe ser nula. Para la partícula 1 tenemos
Para la partícula 2 tenemos
Resolviendo obtenemos
Análisis con rozamiento
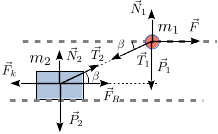
Al incluir el rozamiento debemos añadir una fuerza actuando sobre la partícula 2. La figura de la derecha muestra el diagrama de fuerzas para esta situación. Las fuerzas sobre la partícula 1 tienen las mismas expresiones que antes
Para la partícula 2
Aplicamos de nuevo la condición de equilibrio estático a cada partícula. La diferencia es que tenemos una incógnita mas, la magnitud de la fuerza de rozamiento. Pero ahora la posición de la partícula 2 es un dato. Para la partícula 1 tenemos
Para la partícula 2 tenemos
Resolviendo obtenemos
Utilizando la condición dada por el enunciado , obtenemos para las fuerzas normal y de rozamiento sobre la partícula 2
La condición de no deslizamiento es
Si utilizamos el valor del enunciado la condición queda
Podemos considerar dos situaciones aquí. Por un lado
Por el otro
Por tanto, la condición que debe cumplir la fuerza para que no haya deslizamiento es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 14:41 31 oct 2023 |  | 300 × 137 (18 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:





























![{\displaystyle F\in \left[{\dfrac {2}{3}}kd_{0},2kd_{0}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027ca18f8b883a1fecbd9ee34e1e2c28726ee419)