Intercambio de posiciones en una barca (Ene. 2020 G.I.C.)
Enunciado
Una barca de longitud y masa está en reposo sobre el agua. En el extremo izquierdo de la barca se encuentra una persona de masa . En el extremo derecho hay otra persona de masa . Las dos personas intercambian sus posiciones caminando sobre la barca hacia el extremo opuesto. Si se desprecian las fuerzas que ejerce el agua sobre la barca, ¿cuanto se ha desplazado la barca y hacia donde?
Solución
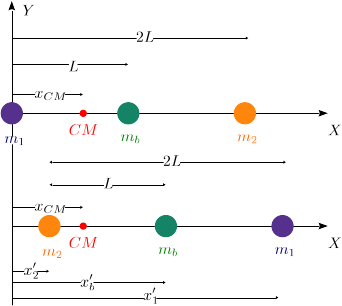
La figura muestra un esquema del problema. En la parte superior están las posiciones de las personas y del centro de la barca, modeladas como masas puntuales. En la parte de abajo están las posiciones después de que las personas intercambien sus posiciones. Como se desprecia la fuerza horizontal que ejerce el agua sobre la barca, la fuerza neta horizontal sobre el sistema formado por las dos personas y la barca es nula. Entonces, la posición horizontal del centro de masas no cambia durante el movimiento interno del sistema.
En la situación inicial la coordenada del centro de masas es
En la situación final la coordenada del centro de masas es
Los dos valores de deben ser iguales.
Esta es la posición del extremo izquierdo de la barca. El valor negativo de indica que la barca se ha movido una distancia hacia la izquierda.









