Diferencia entre las páginas «Archivo:Vuelco-caja-inestable.png» y «Barra con centro deslizando sobre eje, Septiembre 2016 (MR G.I.C.)»
Sin resumen de edición |
|||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Imagen:MR_barra_centro_eje_enunciado.png|right]] | |||
Una barra homogénea delgada (sólido "2") de masa <math>M</math> y longitud <math>2L</math> se mueve de modo que | |||
su centro se encuentra siempre sobre el eje <math>OZ_1</math>. La barra tiene dos grados de libertad de rotación. | |||
El sistema auxiliar <math>OX_0Y_0Z_0</math> se define de modo que la barra esté siempre contenida | |||
en el plano <math>OX_0Z_0</math>. La barra está sometida a la acción de la gravedad, como se indica en | |||
la figura. El contacto de la barra con el eje <math>OZ_1</math> es liso. | |||
#Calcula las reducciones cinematicas en el centro de la barra de los tres movimientos que se pueden definir en el problema. | |||
#Encuentra la expresión del momento cinético de la barra respecto de su centro. | |||
#Encuentra la expresión de la energía cinética de la barra. | |||
#Escribe la Lagrangiana del sistema, así como una integral primera que no sea la energía mecánica. | |||
#En el instante inicial, el centro de la barra se encuentra en el punto <math>O</math> y los valores iniciales de las coordenadas angulares son <math>\theta(0) = \pi/2</math> y <math>\phi(0)=0</math>. La barra se encuentra en reposo. Se ejerce una percusión <math>\hat{\vec{F}} = \hat{F}_0\,(\vec{\jmath}_0 + \vec{k}_0)</math> aplicada en el punto <math>B</math>. Determina los valores de las velocidades generalizadas justo después de la percusión. | |||
= Solución = | |||
== Reducciones cinemáticas == | |||
==== Movimiento {01} ==== | |||
Este es el movimiento de rotación permanente del plano <math>OX_0Z_0</math>. La reducción en el punto <math>O</math> es | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \dot{\phi}\,\vec{k}_0, | |||
\qquad | |||
\vec{v}_{01}^O = \vec{0} | |||
</math> | |||
</center> | |||
Calculamos la velocidad en el punto <math>G</math> usando el Teorema de Chasles | |||
<center> | |||
<math> | |||
\vec{v}_{01}^G = \vec{v}_{01}^O + \vec{\omega}_{01}\times\overrightarrow{OG} | |||
</math> | |||
</center> | |||
Como <math>\overrightarrow{OG} = z\,\vec{k}_0</math>, este vector es paralelo a <math>\vec{\omega}_{01}</math>, el producto vectorial es nulo. La reducción cinemática en el centro de la barra es | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \dot{\phi}\,\vec{k}_0, | |||
\qquad | |||
\vec{v}_{01}^G = \vec{0} | |||
</math></center> | |||
==== Movimiento {20} ==== | |||
Este es el movimiento de la barra respecto del plano <math>OX_0Z_0</math>. La reducción cinemática en el punto <math>G</math> es | |||
<center> | |||
<math> | |||
\vec{\omega}_{20} = \dot{\theta}\,\vec{\jmath}_{0,2} | |||
\qquad | |||
\vec{v}_{01}^G = \dot{z}\,\vec{k}_{0,1} | |||
</math> | |||
</center> | |||
==== Movimiento {21} ==== | |||
Construimos la reducción cinemática usando la composición {21} = {20} + {01}. Para el vector rotación tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = | |||
\dot{\theta}\,\vec{\jmath}_{0} | |||
+ | |||
\dot{\phi}\,\vec{k}_0 | |||
</math> | |||
</center> | |||
Para la velocidad tenemos | |||
<center> | |||
<math> | |||
\vec{v}^G_{21} = \vec{v}^G_{20} + \vec{v}^G_{01} | |||
= | |||
\dot{z}\,\vec{k}_0 | |||
</math> | |||
</center> | |||
== Momento cinético respecto al centro de masas == | |||
El momento cinético respecto al centro de masas se puede calcular con la expresión | |||
<center> | |||
<math> | |||
\vec{L}_G = \overset\leftrightarrow{I}_G\cdot\vec{\omega}_{21} | |||
</math> | |||
</center> | |||
Expresamos el tensor de inercia de la barra en el punto <math>O </math> en la base del sólido solidario con la barra | |||
<center> | |||
<math> | |||
\overset\leftrightarrow{I}_O | |||
= | |||
I | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 0 | |||
\end{array} | |||
\right]_2 | |||
</math> | |||
</center> | |||
con | |||
<center> | |||
<math> | |||
I = \dfrac{1}{3}ML^2 | |||
</math> | |||
</center> | |||
Tenemos que expresar el vector rotación <math>\vec{\omega}_{21}</math> en la base "2" para hacer el producto escalar. Examinando el dibujo tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\imath}_0 = \cos\theta\,\vec{\imath}_2 + \mathrm{sen}\,\theta\,\vec{k}_2\\ | |||
\vec{\jmath}_0 = \vec{\jmath}_2\\ | |||
\vec{k}_0 = -\mathrm{sen}\,\theta\,\vec{\imath}_2 + \cos\theta\,\vec{k}_2 | |||
\end{array} | |||
</math> | |||
</center> | |||
El vector <math>\vec{\omega}_{21}</math> expresado en la base "2" es | |||
<center> | |||
<math> | |||
\vec{\omega}_{21} = -\dot{\phi}\,\mathrm{sen}\,\theta\,\vec{\imath}_2 + \dot{\theta}\,\vec{\jmath}_2 + \dot{\phi}\cos\theta\,\vec{k}_2 | |||
</math> | |||
</center> | |||
El momento angular es | |||
<center> | |||
<math> | |||
\vec{L}_G = | |||
\overset\leftrightarrow{I}_O\cdot\vec{\omega}_{21} | |||
= | |||
I | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 0 | |||
\end{array} | |||
\right]_2 | |||
\left[ | |||
\begin{array}{c} | |||
-\dot{\phi}\,\mathrm{sen}\,\theta\\ | |||
\dot{\theta}\\ | |||
\dot{\phi}\cos\theta | |||
\end{array} | |||
\right]_2 | |||
= | |||
I | |||
\left[ | |||
\begin{array}{c} | |||
-\dot{\phi}\,\mathrm{sen}\,\phi\\ | |||
\dot{\theta}\\ | |||
0 | |||
\end{array} | |||
\right]_2 | |||
</math> | |||
</center> | |||
== Energía cinética de la barra == | |||
Podemos calcularla como suma de la energía cinética de traslación del centro de masa y energía cinética de rotación alrededor de él | |||
<center> | |||
<math> | |||
T = T_{tras} + T_{rot} | |||
</math> | |||
</center> | |||
La energía cinética de traslación es | |||
<center> | |||
<math> | |||
T_{tras} = \dfrac{1}{2}M|\vec{v}_{21}^G|^2 | |||
= | |||
\dfrac{1}{2}M\dot{z}^2 | |||
</math> | |||
</center> | |||
La de rotación es | |||
<center> | |||
<math> | |||
T_{rot} = \dfrac{1}{2}\vec{\omega}_{21}\cdot\overset\leftrightarrow{I}_G\cdot\vec{\omega}_{21} | |||
= | |||
\dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} = \dfrac{1}{6}ML^2\,(\dot{\theta}^2 + \dot{\phi}^2\,\mathrm{sen}^2\,\theta) | |||
</math> | |||
</center> | |||
La energía cinética total es | |||
<center> | |||
<math> | |||
T =\dfrac{1}{2}M|\vec{v}_{21}^G|^2 | |||
+ | |||
\dfrac{1}{6}ML^2\,(\dot{\theta}^2 + \dot{\phi}^2\,\mathrm{sen}^2\,\theta) | |||
</math> | |||
</center> | |||
== Lagrangiana e integral primera == | |||
La barra está sometida al peso (fuerza conservativa) por lo que se puede definir una energía potencial gravitatoria. Tomando como origen el plano <math>OX_0Y_0</math> tenemos | |||
<center> | |||
<math> | |||
U = Mgz | |||
</math> | |||
</center> | |||
y la lagrangiana es | |||
<center> | |||
<math> | |||
L = T- U = \dfrac{1}{2}M\dot{z}^2 | |||
+ | |||
\dfrac{1}{6}ML^2\,(\dot{\theta}^2 + \dot{\phi}^2\,\mathrm{sen}^2\,\theta) | |||
- | |||
mgz | |||
</math> | |||
</center> | |||
Vemos que la coordenada <math>\phi</math> no aparece en la Lagrangiana. Entonces, de la ecuación de Lagrange correspondiente deducimos que su momento generalizado asociado se conserva | |||
<center> | |||
<math> | |||
p_{\phi} = \dfrac{\partial L}{\partial\dot{\phi}} = \dfrac{1}{3}ML^2\dot{\phi}\,\mathrm{sen}^2\,\theta = cte | |||
</math> | |||
</center> | |||
Podemos escribir la integral primera como | |||
<center> | |||
<math> | |||
\dot{\phi}\,\mathrm{sen}^2\,\theta = \dot{\phi}(0)\,\mathrm{sen}^2\,\theta(0) | |||
</math> | |||
</center> | |||
== Movimiento impulsivo == | |||
Lo más sencillo es utilizar las ecuaciones de Lagrange impulsivas. Tenemos tres grados de libertad | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\Delta p_{z} = \hat{Q}_z \\ | |||
\Delta p_{\theta} = \hat{Q}_\theta\\ | |||
\Delta p_{\phi} = \hat{Q}_\phi | |||
\end{array} | |||
</math> | |||
</center> | |||
El sistema parte del reposo, por tanto | |||
<center> | |||
<math> | |||
\dot{z}(0^-) = \dot{\theta}(0^-) = \dot{\phi}(0^-) = 0 | |||
</math> | |||
</center> | |||
Para la coordenada <math>z</math> | |||
<center> | |||
<math> | |||
p_z = \dfrac{\partial L}{\partial\dot{z}} = M\dot{z} | |||
\Longrightarrow | |||
\Delta p_z = M\dot{z}(0^+) - M\dot{z}(0^-) = M\dot{z}(0^+) | |||
</math> | |||
</center> | |||
Para la coordenada <math>\theta</math> | |||
<center> | |||
<math> | |||
p_{\theta} = \dfrac{\partial L}{\partial\dot{\theta}} = \dfrac{1}{3}ML^2\dot{\theta} | |||
\Longrightarrow | |||
\Delta p_{\theta} = \dfrac{1}{3}ML^2\dot{\theta}(0^+) - \dfrac{1}{3}ML^2\dot{\theta}(0^-) = \dfrac{1}{3}ML^2\dot{\theta}(0^+) | |||
</math> | |||
</center> | |||
Para la coordenada <math>\phi</math> | |||
<center> | |||
<math> | |||
p_{\phi} = \dfrac{\partial L}{\partial\dot{\phi}} = \dfrac{1}{3}ML^2\dot{\phi}\,\mathrm{sen}^2\theta | |||
\Longrightarrow | |||
\Delta p_{\phi} = \dfrac{1}{3}ML^2\dot{\phi}(0^+)\,\mathrm{sen}^2\theta(0^+) - \dfrac{1}{3}ML^2\dot{\phi}(0^-)\,\mathrm{sen}^2\theta(0^-) | |||
= | |||
\dfrac{1}{3}ML^2\dot{\phi}(0^+) | |||
</math> | |||
</center> | |||
porque <math>\mathrm{sen}\,\theta(0⁺)= \mathrm{sen}\,(\pi/2) = 1 </math>. | |||
La percusión se aplica en el extremo <math>B</math> de la barra. Necesitamos la velocidad absoluta de ese punto | |||
<center> | |||
<math> | |||
\vec{v}^B_{21} = \vec{v}^G_{21} + \vec{\omega}_{21}\times\overrightarrow{GB} | |||
= | |||
L\dot{\theta}\cos\theta\,\vec{\imath}_0 + L\dot{\phi}\,\mathrm{sen}\,\theta\,\vec{\jmath}_0 + (\dot{z} - L\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{k}_0 | |||
</math> | |||
</center> | |||
Hemos usado que | |||
<center> | |||
<math> | |||
\overrightarrow{GB} = L\,\mathrm{sen}\,\theta\,\vec{\imath}_0 + L\cos\theta\,\vec{k}_0 | |||
</math> | |||
</center> | |||
Las fuerzas generalizadas son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\hat{Q}_z = \hat{\vec{F}}\cdot\dfrac{\partial\vec{v}^B_{21}}{\partial\dot{z}}= \hat{F}_0 \\ | |||
\hat{Q}_{\theta} = \hat{\vec{F}}\cdot\dfrac{\partial\vec{v}^B_{21}}{\partial\dot{\theta}} = | |||
-L\hat{F}_0\,\mathrm{sen}\,\theta(0) = -L\hat{F}_0 | |||
\\ | |||
\hat{Q}_{\phi} = \hat{\vec{F}}\cdot\dfrac{\partial\vec{v}^B_{21}}{\partial\dot{\phi}} = | |||
L\hat{F}_0\,\mathrm{sen}\,\theta(0) = L\hat{F}_0 | |||
\end{array} | |||
</math> | |||
</center> | |||
Aplicando las ecuaciones de Lagrange impulsivas tenemos | |||
<center> | |||
<math> | |||
\dot{z}(0^+) = \dfrac{\hat{F}_0}{M}, | |||
\qquad | |||
\dot{\theta}(0^+) = -\dfrac{3\hat{F}_0}{ML}, | |||
\qquad | |||
\dot{\phi}(0^+) = \dfrac{3\hat{F}_0}{ML} | |||
</math> | |||
</center> | |||
Estos son las condiciones iniciales del movimiento ulterior de la barra después de la percusión. | |||
[[Categoría:Problemas de Dinámica Vectorial del Sólido Rígido]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión del 18:16 25 oct 2023
Enunciado
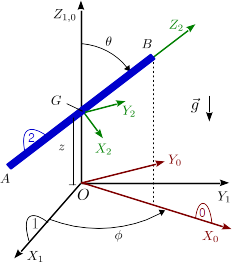
Una barra homogénea delgada (sólido "2") de masa y longitud se mueve de modo que su centro se encuentra siempre sobre el eje . La barra tiene dos grados de libertad de rotación. El sistema auxiliar se define de modo que la barra esté siempre contenida en el plano . La barra está sometida a la acción de la gravedad, como se indica en la figura. El contacto de la barra con el eje es liso.
- Calcula las reducciones cinematicas en el centro de la barra de los tres movimientos que se pueden definir en el problema.
- Encuentra la expresión del momento cinético de la barra respecto de su centro.
- Encuentra la expresión de la energía cinética de la barra.
- Escribe la Lagrangiana del sistema, así como una integral primera que no sea la energía mecánica.
- En el instante inicial, el centro de la barra se encuentra en el punto y los valores iniciales de las coordenadas angulares son y . La barra se encuentra en reposo. Se ejerce una percusión aplicada en el punto . Determina los valores de las velocidades generalizadas justo después de la percusión.
Solución
Reducciones cinemáticas
Movimiento {01}
Este es el movimiento de rotación permanente del plano . La reducción en el punto es
Calculamos la velocidad en el punto usando el Teorema de Chasles
Como , este vector es paralelo a , el producto vectorial es nulo. La reducción cinemática en el centro de la barra es
Movimiento {20}
Este es el movimiento de la barra respecto del plano . La reducción cinemática en el punto es
Movimiento {21}
Construimos la reducción cinemática usando la composición {21} = {20} + {01}. Para el vector rotación tenemos
Para la velocidad tenemos
Momento cinético respecto al centro de masas
El momento cinético respecto al centro de masas se puede calcular con la expresión
Expresamos el tensor de inercia de la barra en el punto en la base del sólido solidario con la barra
con
Tenemos que expresar el vector rotación en la base "2" para hacer el producto escalar. Examinando el dibujo tenemos
El vector expresado en la base "2" es
El momento angular es
Energía cinética de la barra
Podemos calcularla como suma de la energía cinética de traslación del centro de masa y energía cinética de rotación alrededor de él
La energía cinética de traslación es
La de rotación es
La energía cinética total es
Lagrangiana e integral primera
La barra está sometida al peso (fuerza conservativa) por lo que se puede definir una energía potencial gravitatoria. Tomando como origen el plano tenemos
y la lagrangiana es
Vemos que la coordenada no aparece en la Lagrangiana. Entonces, de la ecuación de Lagrange correspondiente deducimos que su momento generalizado asociado se conserva
Podemos escribir la integral primera como
Movimiento impulsivo
Lo más sencillo es utilizar las ecuaciones de Lagrange impulsivas. Tenemos tres grados de libertad
El sistema parte del reposo, por tanto
Para la coordenada
Para la coordenada
Para la coordenada
porque Error al representar (error de sintaxis): {\displaystyle \mathrm{sen}\,\theta(0⁺)= \mathrm{sen}\,(\pi/2) = 1 } .
La percusión se aplica en el extremo de la barra. Necesitamos la velocidad absoluta de ese punto
Hemos usado que
Las fuerzas generalizadas son
Aplicando las ecuaciones de Lagrange impulsivas tenemos
Estos son las condiciones iniciales del movimiento ulterior de la barra después de la percusión.
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 17:01 17 oct 2023 |  | 413 × 384 (16 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:




















![{\displaystyle {\overset {\leftrightarrow }{I}}_{O}=I\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2578002b592ea6a3a3a6206f1f5b15d910f7767)




![{\displaystyle {\vec {L}}_{G}={\overset {\leftrightarrow }{I}}_{O}\cdot {\vec {\omega }}_{21}=I\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}}\right]_{2}\left[{\begin{array}{c}-{\dot {\phi }}\,\mathrm {sen} \,\theta \\{\dot {\theta }}\\{\dot {\phi }}\cos \theta \end{array}}\right]_{2}=I\left[{\begin{array}{c}-{\dot {\phi }}\,\mathrm {sen} \,\phi \\{\dot {\theta }}\\0\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b83def8bb2511490385370388ef2362fb15403)




















