Diferencia entre las páginas «Barra articulada en otra barra, Noviembre 2012 (G.I.C.)» y «Dos masas en un triángulo, Noviembre 2012 (G.I.C.)»
(Diferencia entre las páginas)
Última edición de la página hace 5 meses por Pedro
(Página creada con «== Enunciado == right Una barra de radio <math>R</math> gira alrededor de uno de sus extremos, situado en el punto <math>O</math>. En su otro extremo se articula otra barra de longitud <math>R</math> que a su vez gira en con la misma velocidad angular. #Expresa el vector de posición <math>\overrightarrow{OP}</math> en función del ángulo <math>\theta</math> de la figura. #Si <math>\dot{\theta}=\omega</math> y el módu…») |
(Página creada con «==Enunciado== right Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m. === Solución=== right Como indica la figura, cada masa M atrae a la masa m con una fuerza dirigida hacia ella. La fuerza neta es la sum…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | ==Enunciado== | ||
[[Imagen: | [[Imagen:F1_GIC_PPC_triangulo_enunciado.png|right]] | ||
Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m. | |||
=== Solución=== | |||
[[Imagen:F1_GIC_PPC_triangulo_fuerzas.png|right]] | |||
Como indica la figura, cada masa M atrae a la masa m con una fuerza dirigida hacia ella. La fuerza neta es la suma vectorial de estas dos fuerzas. Al hacer la suma vectorial, sólo queda la componente vertical de cada fuerza. | |||
El módulo de la fuerza con que una masa M atrae a la masa m es | |||
El | |||
<center> | <center> | ||
<math> | <math> | ||
|\vec{ | |\vec{F}| = \dfrac{G\,M\,m}{d^2} | ||
</math> | </math> | ||
</center> | </center> | ||
La proyección de esta fuerza sobre la vertical es | |||
<center> | <center> | ||
<math> | <math> | ||
F_{vert} = |\vec{F}|\cos\alpha = \dfrac{G\,M\,m}{d^2}\,\cos\alpha | |||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
= | Como el triángulo es equilátero, el ángulo es <math>\alpha = \pi/6 </math>. La fuerza total es la suma de las dos proyecciones. | ||
La | |||
<center> | <center> | ||
<math> | <math> | ||
\ | F_m = 2\,F_{vert} = \dfrac{2\,G\,M\,m}{d^2}\,\cos\alpha | ||
=\dfrac{\sqrt{3}\,G\,M\,m}{d^2} = | |||
12\times10^{-12}\,\mathrm{N} = 12\,\mathrm{pN} | |||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría: | [[Categoría:Dinámica del punto material|1]] | ||
[[Categoría:Problemas de examen]] | [[Categoría:Problemas de examen]] | ||
[[Categoría:Física I (G.I.C.)]] | [[Categoría:Física I (G.I.C.)]] | ||
Revisión actual - 18:24 25 oct 2023
Enunciado

Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m.
Solución
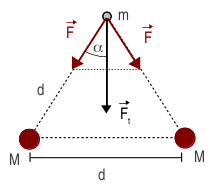
Como indica la figura, cada masa M atrae a la masa m con una fuerza dirigida hacia ella. La fuerza neta es la suma vectorial de estas dos fuerzas. Al hacer la suma vectorial, sólo queda la componente vertical de cada fuerza.
El módulo de la fuerza con que una masa M atrae a la masa m es
La proyección de esta fuerza sobre la vertical es
Como el triángulo es equilátero, el ángulo es . La fuerza total es la suma de las dos proyecciones.



