Diferencia entre las páginas «Partícula con movimiento rectilíneo, Noviembre 2012 (G.I.C.)» y «Barra articulada en otra barra, Noviembre 2012 (G.I.C.)»
(Página creada con «== Enunciado== Una partícula realiza un movimiento unidimensional, de modo que su velocidad y aceleración cumplen la relación <math>a(t)\,v(t) = 3C^2t^2/2</math>, siendo <math>C</math> una constante. #¿Cuales son las dimensiones de la constante <math>C</math>? #Si la velocidad inicial es <math>v(0)=v_0</math>, ¿cuál es la expresión de la velocidad en cualquier instante de tiempo? #Supongamos que <math>v_0=0</math> y la posición inicial de la partícula es <mat…») |
(Página creada con «== Enunciado == right Una barra de radio <math>R</math> gira alrededor de uno de sus extremos, situado en el punto <math>O</math>. En su otro extremo se articula otra barra de longitud <math>R</math> que a su vez gira en con la misma velocidad angular. #Expresa el vector de posición <math>\overrightarrow{OP}</math> en función del ángulo <math>\theta</math> de la figura. #Si <math>\dot{\theta}=\omega</math> y el módu…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado== | == Enunciado == | ||
Una | [[Imagen:F1_GIC_PPC_doble_barra_enunciado.png|right]] | ||
Una barra de radio <math>R</math> gira alrededor de uno de sus extremos, situado en el punto <math>O</math>. En su otro extremo se articula otra barra de longitud <math>R</math> que a su vez gira en con la misma velocidad angular. | |||
= | #Expresa el vector de posición <math>\overrightarrow{OP}</math> en función del ángulo <math>\theta</math> de la figura. | ||
#Si <math>\dot{\theta}=\omega</math> y el módulo de la velocidad del punto <math>P</math> es <math>v_0</math>, encuentra el valor de <math>\omega</math>. | |||
#Calcula el vector normal en cada punto de la trayectoria de <math>P</math>. | |||
#Calcula la curvatura en cada punto de la trayectoria. | |||
== | == Solución== | ||
=== Vector de posición=== | |||
El vector de posición del punto <math> P</math> puede construirse como la suma | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{OP} = \overrightarrow{OA} + \overrightarrow{AP} | |||
</math> | </math> | ||
</center> | </center> | ||
Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{OA} = R\,\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Por otro lado | |||
<center> | |||
<math> | |||
\overrightarrow{AP} = -R\,\mathrm{sen}\,\theta\,\vec{\imath} + R\cos\theta\,\vec{\jmath} | |||
</math> | |||
</center> | |||
Por tanto el vector buscado es | |||
<center> | |||
<math> | |||
\overrightarrow{OP} = R\,(\cos\theta - \mathrm{sen}\,\theta\,)\,\vec{\imath} | |||
+ R\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath} | |||
</math> | </math> | ||
</center> | </center> | ||
=== Velocidad | === Velocidad angular=== | ||
Derivamos respecto al tiempo el vector de posición para obtener el vector velocidad | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{v} = \dot{\overrightarrow{OP}} = | |||
-R\,\dot{\theta}\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\imath} | |||
+ | |||
R\,\dot{\theta}\,(\cos\theta - \mathrm{sen}\,\theta)\,\vec{\jmath} | |||
</math> | </math> | ||
</center> | </center> | ||
El módulo de este vector es | |||
<center> | <center> | ||
<math> | <math> | ||
v\,\ | |\vec{v}| = R\,\dot\theta\,\sqrt{\mathrm{sen}^2\theta + \cos^2\theta + 2\,\mathrm{sen}\,\theta\cos\theta + | ||
\mathrm{sen}^2\theta + \cos^2\theta - 2\,\mathrm{sen}\,\theta\cos\theta | |||
} | |||
=\sqrt{2}\,R\,\dot{\theta} | |||
=\sqrt{2}\,R\,\omega | |||
</math> | </math> | ||
</center> | </center> | ||
El enunciado nos dice que este módulo vale <math>v_0 </math>. Por tanto | |||
<center> | <center> | ||
<math> | <math> | ||
\omega = \dfrac{v_0}{\sqrt{2}\,R} | |||
</math> | </math> | ||
</center> | </center> | ||
=== Vector normal=== | |||
Podemos calcular el vector normal a partir de la aceleración. Para simplificar, consideramos que <math>v_0 </math> es constante, por lo que componente tangencial de la aceleración es nula y la aceleración es íntegramente normal. Teniendo en cuenta que en este caso <math>\dot{\theta}=\omega </math> es constante tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \vec{a}= \dot{\vec{v}} = | ||
-R\,\dot{\theta}^2\,(\cos\theta - \mathrm{sen}\,\theta)\,\vec{\imath} | |||
-R\,\dot{\theta}^2\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath} | |||
</math> | </math> | ||
</center> | </center> | ||
El vector normal es | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{N} = \dfrac{\vec{a}}{|\vec{a}|} | |||
</math> | </math> | ||
</center> | </center> | ||
Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
|\vec{a}| = \sqrt{2}\,R\,\omega^2 | |||
</math> | </math> | ||
</center> | </center> | ||
Por | Por tanto | ||
<center> | <center> | ||
<math> | <math> | ||
\vec{N}= | |||
\dfrac{\mathrm{sen}\,\theta-\cos\theta}{\sqrt{2}}\,\vec{\imath} | |||
- | |||
\dfrac{\cos\theta + \mathrm{sen}\,\theta}{\sqrt{2}}\,\vec{\jmath} | |||
</math> | </math> | ||
</center> | </center> | ||
=== Curvatura=== | |||
La curvatura es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \kappa = \dfrac{a_N}{v^2} | ||
</math> | </math> | ||
</center> | </center> | ||
En este caso <math>a_N = |\vec{a}|=\sqrt{2}\,R\,\omega^2 </math>. Por tanto | |||
<center> | <center> | ||
<math> | <math> | ||
\kappa = \dfrac{1}{\sqrt{2}\,R} | |||
</math> | </math> | ||
</center> | </center> | ||
Como es una curva plana y la curvatura es constante, la trayectoria es una circunferencia de radio <math>\sqrt{2}\,R </math>. | |||
[[Categoría:Problemas de cinemática del punto]] | [[Categoría:Problemas de cinemática del punto]] | ||
[[Categoría:Problemas de examen]] | [[Categoría:Problemas de examen]] | ||
[[Categoría:Física I (G.I.C.)]] | [[Categoría:Física I (G.I.C.)]] | ||
Revisión actual - 18:23 25 oct 2023
Enunciado
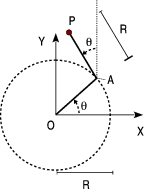
Una barra de radio gira alrededor de uno de sus extremos, situado en el punto . En su otro extremo se articula otra barra de longitud que a su vez gira en con la misma velocidad angular.
- Expresa el vector de posición en función del ángulo de la figura.
- Si y el módulo de la velocidad del punto es , encuentra el valor de .
- Calcula el vector normal en cada punto de la trayectoria de .
- Calcula la curvatura en cada punto de la trayectoria.
Solución
Vector de posición
El vector de posición del punto puede construirse como la suma
Tenemos
Por otro lado
Por tanto el vector buscado es
Velocidad angular
Derivamos respecto al tiempo el vector de posición para obtener el vector velocidad
El módulo de este vector es
El enunciado nos dice que este módulo vale . Por tanto
Vector normal
Podemos calcular el vector normal a partir de la aceleración. Para simplificar, consideramos que es constante, por lo que componente tangencial de la aceleración es nula y la aceleración es íntegramente normal. Teniendo en cuenta que en este caso es constante tenemos
El vector normal es
Tenemos
Por tanto
Curvatura
La curvatura es
En este caso . Por tanto
Como es una curva plana y la curvatura es constante, la trayectoria es una circunferencia de radio .






















