Diferencia entre las páginas «Archivo:Rotacion-base-90-05.png» y «Partícula en aro con diferentes métodos (MRGIC)»
Sin resumen de edición |
(Página creada con «= Enunciado = == Partícula en aro con diferentes métodos== sinmarco|derecha Se tiene un aro circular de radio <math>R</math> contenido en un plano vertical. Engarzado en él hay una masa <math>m</math> que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad. # Suponiendo que el contacto es liso, encuentra las ecuación de movimiento de la masa usando…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
== [[Partícula en aro con diferentes métodos (MRGIC) | Partícula en aro con diferentes métodos]]== | |||
[[Archivo:ParticulaAro.png|sinmarco|derecha]] | |||
Se tiene un aro circular de radio <math>R</math> contenido en un plano vertical. Engarzado en él hay una masa <math>m</math> que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad. | |||
# Suponiendo que el contacto es liso, encuentra las ecuación de movimiento de la masa usando el Principio de D'Alembert. | |||
# Repite el primer apartado usando la energía cinética y fuerzas generalizadas. | |||
# Repite el primer apartado usando la Función de Lagrange. | |||
# Repite el primer apartado usando el Prinicipio de Liberación. | |||
# Repite el primer apartado usando la técnica de los multiplicadores de Lagrange. | |||
# Consideremos ahora que el vínculo entre la partícula y el aro es rugoso, con un coeficiente de rozamiento dinámico <math>\mu</math>. Determina las ecuaciones de movimiento usando el Principio de Liberación. | |||
= Solución = | |||
== Principio de D'Alembert == | |||
[[Archivo:ParticulaAroDAlembert.png|sinmarco|derecha]] | |||
Primero identificamos el número de grados de libertad. La partícula está sometida a dos vínculos. Usando coordenadas cilíndricas estos vínculos se expresan | |||
<center> | |||
<math> | |||
r = R, \qquad z=0. | |||
</math> | |||
</center> | |||
Por tanto, la partícula tiene un grado de libertad. Vamos a usar la coordenada <math>\theta </math> para trabajar. Los vectores de posición, velocidad y aceleración en coordenadas cilíndricas son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{r} = R\,\vec{u}_{r},\\ | |||
\vec{v} = R\dot{\theta}\,\vec{u}_{\theta},\\ | |||
\vec{a} = -R\dot{\theta}^2\,\vec{u}_r + R\ddot{\theta}\,\vec{u}_{\theta}. | |||
\end{array} | |||
</math> | |||
</center> | |||
La única fuerza aplicada es el peso, como se indica en la figura. Proyectándolo cilíndricas tenemos | |||
<center> | |||
<math> | |||
\vec{P}_m = mg\cos\theta\,\vec{u}_r - mg\,\mathrm{sen}\,\theta\,\vec{u}_{\theta}. | |||
</math> | |||
</center> | |||
El Principio de D'Alembert establece que, en cualquier desplazamiento virtual, debe cumplirse | |||
<center> | |||
<math> | |||
(\vec{P}_m - m\vec{a})\cdot\delta\vec{r} = 0. | |||
</math> | |||
</center> | |||
Como sólo hay un grado de libertad, el desplazamiento virtual mas general es | |||
<center> | |||
<math> | |||
\delta\vec{r} = \left(\dfrac{\partial \vec{r}}{\partial\theta}\right)\,\delta\theta | |||
= | |||
R\,\dfrac{\partial\vec{u}_r}{\partial\theta}\,\delta\theta = R\delta\theta\,\vec{u}_{\theta}. | |||
</math> | |||
</center> | |||
Recordemos que en coordenadas cilíndricas se tiene | |||
<center> | |||
<math> | |||
\dfrac{\partial\vec{u}_r}{\partial\theta} = \vec{u}_{\theta}, \qquad | |||
\dfrac{\partial\vec{u}_{\theta}}{\partial\theta} = -\vec{u}_{r}. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{P}_m - m\vec{a} = m(g\cos\theta - R\dot{\theta}^2)\,\vec{u}_r - m(g\mathrm{sen}\,\theta + R\ddot{\theta})\,\vec{u}_{\theta}. | |||
</math> | |||
</center> | |||
Aplicando el Principio de D'Alembert, obtenemos la ecuación de movimiento | |||
<center> | |||
<math> | |||
R\ddot{\theta} + g\,\mathrm{sen}\,\theta = 0. | |||
</math> | |||
</center> | |||
== Con la energía cinética == | |||
Al haber sólo un grado de libertad, hay una sola ecuación de Lagrange | |||
<center> | |||
<math> | |||
\dfrac{\mathrm{d}T}{\mathrm{d}t}\left(\dfrac{\partial T}{\partial\dot{\theta}}\right) - \dfrac{\partial T}{\partial\theta} = Q_{\theta}. | |||
</math> | |||
</center> | |||
La energía cinética es | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}m|\vec{v}|^2 = \dfrac{1}{2}mR^2\dot{\theta}^2. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\dfrac{\partial T}{\partial\dot{\theta}} = mR^2\dot{\theta} | |||
\Rightarrow | |||
\dfrac{\mathrm{d}T}{\mathrm{d}t}\left(\dfrac{\partial T}{\partial\dot{\theta}}\right) = mR^2\ddot{\theta}, | |||
\\ | |||
\dfrac{\partial T}{\partial\theta} = 0. | |||
\end{array} | |||
</math> | |||
</center> | |||
La fuerza generalizada es debida a la acción del peso. Es decir | |||
<center> | |||
<math> | |||
Q_{\theta} = \vec{P}_m\cdot\dfrac{\partial\vec{r}}{\partial\theta} = -mgR\,\mathrm{sen}\,\theta. | |||
</math> | |||
</center> | |||
Finalmente, la ecuación de movimiento es, nuevamente | |||
<center> | |||
<math> | |||
R\ddot{\theta} + g\,\mathrm{sen}\,\theta = 0. | |||
</math> | |||
</center> | |||
== Con la función de Lagrange == | |||
Al ser el peso una fuerza conservativa, podemos asignarle una energía potencial. Tomando como altura de referencia el centro del aro, tenemos | |||
<center> | |||
<math> | |||
U = -mgR\cos\theta. | |||
</math> | |||
</center> | |||
La función de Lagrange es | |||
<center> | |||
<math> | |||
L = T - U = \dfrac{1}{2}mR^2\dot{\theta}^2 + mgR\cos\theta. | |||
</math> | |||
</center> | |||
La ecuación de Lagrange es | |||
<center> | |||
<math> | |||
\dfrac{\mathrm{d}T}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right) - \dfrac{\partial L}{\partial\theta} = 0. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\dfrac{\partial L}{\partial\dot{\theta}} = mR^2\dot{\theta} | |||
\Rightarrow | |||
\dfrac{\mathrm{d}L}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right) = mR^2\ddot{\theta}, | |||
\\ | |||
\dfrac{\partial L}{\partial\theta} = -mgR\,\mathrm{sen}\,\theta. | |||
\end{array} | |||
</math> | |||
</center> | |||
Por tanto la ecuación de movimiento es, de nuevo | |||
<center> | |||
<math> | |||
R\ddot{\theta} + g\,\mathrm{sen}\,\theta = 0. | |||
</math> | |||
</center> | |||
Revisión del 15:01 29 nov 2023
Enunciado
Partícula en aro con diferentes métodos

Se tiene un aro circular de radio contenido en un plano vertical. Engarzado en él hay una masa que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad.
- Suponiendo que el contacto es liso, encuentra las ecuación de movimiento de la masa usando el Principio de D'Alembert.
- Repite el primer apartado usando la energía cinética y fuerzas generalizadas.
- Repite el primer apartado usando la Función de Lagrange.
- Repite el primer apartado usando el Prinicipio de Liberación.
- Repite el primer apartado usando la técnica de los multiplicadores de Lagrange.
- Consideremos ahora que el vínculo entre la partícula y el aro es rugoso, con un coeficiente de rozamiento dinámico . Determina las ecuaciones de movimiento usando el Principio de Liberación.
Solución
Principio de D'Alembert
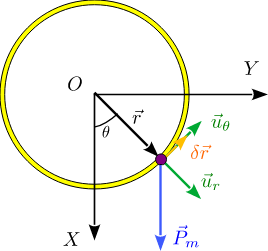
Primero identificamos el número de grados de libertad. La partícula está sometida a dos vínculos. Usando coordenadas cilíndricas estos vínculos se expresan
Por tanto, la partícula tiene un grado de libertad. Vamos a usar la coordenada para trabajar. Los vectores de posición, velocidad y aceleración en coordenadas cilíndricas son
La única fuerza aplicada es el peso, como se indica en la figura. Proyectándolo cilíndricas tenemos
El Principio de D'Alembert establece que, en cualquier desplazamiento virtual, debe cumplirse
Como sólo hay un grado de libertad, el desplazamiento virtual mas general es
Recordemos que en coordenadas cilíndricas se tiene
Tenemos
Aplicando el Principio de D'Alembert, obtenemos la ecuación de movimiento
Con la energía cinética
Al haber sólo un grado de libertad, hay una sola ecuación de Lagrange
La energía cinética es
Tenemos
La fuerza generalizada es debida a la acción del peso. Es decir
Finalmente, la ecuación de movimiento es, nuevamente
Con la función de Lagrange
Al ser el peso una fuerza conservativa, podemos asignarle una energía potencial. Tomando como altura de referencia el centro del aro, tenemos
La función de Lagrange es
La ecuación de Lagrange es
Tenemos
Por tanto la ecuación de movimiento es, de nuevo
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 14:43 29 nov 2023 |  | 1500 × 1405 (44 kB) | Antonio (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:



















