Diferencia entre las páginas «Esfera en recipiente cilíndrico» y «Problemas de Dinámica Analítica (MR G.I.C.)»
Secciones
Sin resumen de edición |
|||
| Línea 1: | Línea 1: | ||
= | = Problemas del boeltín = | ||
< | ==[[ Engranaje sobre cremallera (MR G.I.C.) | Engranaje sobre cremallera ]]== | ||
[[Imagen:MR_engranaje_cremallera.png|right]] | |||
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en <math>B</math>. El deslizador está acoplado a un muelle, de constante elástica <math>k</math>, que se encuentra relajado cuando <math>x=2R</math>. En ese instante se tiene <math>\theta=0</math>. Las masas del engranaje, el deslizador y la cremallera son la misma e igual a <math>m</math>. El radio de giro del engranaje es <math>r_c</math>. El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura. | |||
#Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento. | |||
#Encuentra las ecuaciones diferenciales del movimiento. | |||
==[[Triciclo (MR) | Triciclo]]== | |||
< | ==[[ Dos partículas unidas por una barra sin masa con una cuchilla, (MR) | Dos partículas unidas por una barra sin masa con una cuchilla]] == | ||
[[Imagen:MR_Masas_cuchilla.png|right]] | |||
Dos partículas puntuales de masa <math>m</math> están unidas por una barra de longitud <math>L</math> y masa despreciable. Las partículas deslizan sobre un plano fijo <math>OX_1Y_1</math>, pero una de las partículas tiene una cuchilla, de modo que su velocidad sólo puede tener componente paralela a la cuchilla. Una fuerza <math>\vec{F}=F_0\,\vec{\imath}_1</math> constante actúa sobre la partícula que no tiene la cuchilla. | |||
#Encuentra la expresión del vínculo no holónomo del sistema. | |||
#Escribe las ecuaciones de Lagrange utilizando la técnica de los multiplicadores de Lagrange. | |||
#Identifica el significado físico del multiplicador de Lagrange. | |||
= Otros problemas = | |||
< | ==[[Deslizadera y disco rodando sin deslizar (MR G.I.C.) | Deslizadera y disco rodando sin deslizar]]== | ||
[[File:MR_disco_deslizadera_enunciado.png|right]] | |||
Un disco homogéneo (sólido "2") de masa <math>m</math> y radio <math>R</math> puede rotar alrededor de su | |||
centro <math>C</math>, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa <math>m</math> | |||
puede moverse a lo largo del | |||
eje <math>O_1Y_1</math>, de modo que en el punto de contacto <math>A</math> el disco rueda sin deslizar sobre el | |||
sólido "0". La deslizadera está conectada a un muelle de constante elástica <math>k</math> y | |||
longitud natural <math>l_0</math>. El otro extremo del muelle está anclado en un punto fijo del eje | |||
<math>O_1X_1</math>, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura. | |||
#¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales. | |||
#Calcula las energías cinética y potencial del sistema en función de sus grados de libertad. | |||
#Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento. | |||
#Se aplica sobre el disco un par de fuerzas externo <math>\vec{\tau} = \tau_0\cos(\omega t)\,\vec{k}_1</math>. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de <math>\omega</math> aparece una resonancia mecánica? | |||
#Ahora no hay par aplicado. Se aplica una percusión <math>\vec{\hat{F}}=[\hat{F}_0, \hat{F}_0,0]_1</math> sobre el punto <math>B</math> del sólido "2". En el instante de la percusión se cumple <math>s(0)=l_0</math>, <math>\theta(0)=0</math>, <math>\dot{s}(0^-)=0</math>, <math>\dot{\theta}(0^-)=0</math>. Calcula el estado del sistema inmediatamente después de la percusión. | |||
< | ==[[Aro colgando de una barra que rota, Enero 2015 (MR G.I.C.)|Aro colgando de una barra que rota ]] == | ||
[[Imagen:MR_aro_colgando_barra_enunciado.png|right]] | |||
La barra homogénea <math>OA</math> (sólido "0") tiene masa <math>m</math> y longitud <math>L</math>. Está articulada en el punto | |||
fijo <math>O</math> y rota de modo que está siempre contenida en el plano <math>OX_1Y_1</math>. En su extremo <math>A</math> está articulado un aro homogéneo de radio <math>R</math> y masa <math>m</math> (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos <math>\{\theta, \psi\}</math> como coordenadas para resolver el problema. | |||
#Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}. | |||
#Calcula las energías cinética y potencial totales del sistema. | |||
#Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento. | |||
#Se impone el vínculo cinemático <math>\dot{\theta}=\omega_0</math>. Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene <math>\theta(0)=0</math>, <math>\psi(0)=0</math>. | |||
#Supongamos que las coordenadas <math>\{\theta, \psi\}</math> son de nuevo libres. Supón que se tiene <math>\theta(0)=0</math>, <math>\psi(0)=0</math>. En ese instante una percusión <math>\vec{\hat{F}}=[\hat{F}_0,\hat{F}_0,0]_1</math> actúa sobre el punto <math>A</math>. Determina el estado cinemático del sistema justo después de la percusión. | |||
==[[ Sep. 2018 (M.R.) Barra rotando alrededor de barra horizontal con muelle | Barra rotando alrededor de barra horizontal con muelle]]== | |||
[[Imagen:MR_2018_barras_muelle_enunciado.png|right]] | |||
Una barra de longitud <math>2d</math> y masa despreciable (sólido "0") puede rotar alrededor del eje <math>OZ_1</math>. El punto <math>O</math> de la barra es fijo. La barra "0" siempre está contenida en el plano <math>OX_1Y_1</math>. Otra barra, también de longitud <math>2d</math> y masa <math>m</math> (sólido "2"), está conectada a la barra "0" por un pasador en el punto <math>A</math>. El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica <math>k</math> y longitud natural nula <math>l_0=d</math> conecta los puntos <math>O</math> y <math>A</math>. | |||
#Determina las reducciones cinemáticas <math>\{01\}, \{20\}</math> y <math>\{21\}</math> en <math>G</math>. | |||
#Calcula el momento cinético de la barra "2" respecto de <math>G</math>. | |||
#A partir de ahora suponemos que <math>\phi=\dot{\phi}=\ddot{\phi}=0</math>, es decir, la coordenada <math>\phi</math> ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema. | |||
#En <math>t=0</math> tenemos <math>s(0)=d</math>, <math>\theta(0)=-\pi/2</math>, <math>\dot{s}(0)=0</math> y <math>\dot{\theta}=0</math> (<math>\phi</math> sigue estando fijada). La barra "2" recibe una percusión <math>\vec{\hat{F}} = [\hat{F}_0, 0, \hat{F}_0]_1</math> en el punto B. Determina el estado del sistema justo después de la percusión. | |||
< | ==[[ Disco rodando sobre plataforma con muelle (Ene 2018 MR) | Disco rodando sobre plataforma con muelle ]]== | ||
[[Imagen:MR_disco_placa_muelle_enunciado.png|right]] | |||
Un disco de masa <math>m</math> y radio <math>R</math> (sólido "2") rueda sin deslizar sobre una placa | |||
rectangular de masa <math>m</math> (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo | |||
<math>O_1X_1</math>. Un muelle de constante elástica <math>k</math> y longitud natural nula conecta la placa con | |||
el eje <math>O_1Y_1</math>. | |||
#Encuentra la reducción cinemática del movimiento absoluto. | |||
#Escribe la Lagrangiana del sistema. | |||
#Escribe las ecuaciones de Lagrange. | |||
#En el estado inicial los dos sólidos están en reposo y <math>x_0(0)=0</math>, <math>x_2(0)=L/2</math>. Se somete la placa a una percusión <math>\vec{\hat{F}} = \hat{F}_0\,\vec{\imath}_1</math> aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión? | |||
y | ==[[Disco rodando en cavidad con muelle de torsión MR Dic 2016/17 | Disco rodando en cavidad con muelle de torsión]]== | ||
[[Imagen:MR_disco_cavidad_muelle_torsion_enunciado.png|right]] | |||
Un disco de radio <math>R</math> y masa <math>m</math> (sólido "2") rueda sin deslizar sobre | |||
una superficie circular cóncava (sólido "1") de radio <math>3R</math>. En el centro del | |||
disco se articula una barra (sólido "0") de masa despreciable y longitud <math>2R</math>. El otro | |||
extremo de la barra se articula en un punto fijo <math>O</math>. La barra está conectada | |||
a su vez a un resorte de torsión en el punto <math>O</math>. Este resorte ejerce | |||
un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él | |||
se puede expresar como <math>U_k = k \phi^2</math>, siendo <math>k</math> una constante. | |||
#Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre <math>\dot{\phi}</math> y <math>\dot{\psi}</math>?. | |||
#Calcula la energía cinética del disco y su energía potencial. | |||
#Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo <math>\phi</math> es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación. | |||
#Estando el disco en reposo y con <math>\phi=0</math>, se aplica al centro del disco una percusión <math>\hat{\vec{F}} = \hat{F}_0\,\vec{\jmath}_0</math>. Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje. | |||
< | ==[[Barra con muelle horizontal, Febrero 2016 (MR G.I.C.) | Barra con muelle horizontal]]== | ||
[[Imagen:MR_GIC_Barra_muelle_horizontal.png|right]] | |||
Una barra de longitud <math>2a</math> y masa <math>m</math> (sólido "2") desliza con un extremo (punto <math>A</math>) apoyado sobre un plano horizontal liso. El extremo <math>A</math> está unido a un muelle de constante elástica k y longitud natural nula anclado en <math>C</math> que se mantiene siempre horizontal. La gravedad actúa verticalmente hacia abajo. En <math>t=0</math> la barra estaba en reposo, el punto <math>A</math> coincidía con <math>O_1</math> y la barra estaba completamente vertical. | |||
# Encuentra la expresión que da la cantidad de movimiento de la barra. | |||
# Encuentra la expresión que da el momento cinético de la barra respecto del punto <math>A </math>. | |||
#Determina las ecuaciones de movimiento del sistema. | |||
#¿Cómo es la fuerza de ligadura en el punto <math>A </math>? | |||
#Supongamos que se fuerza al punto <math>A</math> a moverse con velocidad uniforme <math>\vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1</math>. ¿Cual de estas fuerzas aplicadas en <math>A</math> consigue ese efecto? | |||
== | ==[[Placa cuadrada pivotando con muelle, Septiembre 2016 (MR G.I.C.)|Placa cuadrada pivotando con muelle ]] == | ||
[[Imagen:MR_Placa_cuadrada_muelle_enunciado.png|right]] | |||
El sólido "2' es una placa cuadrada y homogénea, de lado <math>2d</math> y masa <math>M</math>. La placa está articulada en | |||
su vértice <math>A</math>, que permanece fijo. El vértice <math>C</math> de la placa está conectado a un muelle de constante elástica <math>k</math> y | |||
longitud natural nula, anclado en el punto <math>O_1</math>. En el instante inicial la posición de la placa está | |||
indicada en la figura por el cuadrado punteado. En esa posición inicial, el lado <math>AB_0</math> no está apoyado | |||
en ninguna superficie. La gravedad actúa en la dirección vertical hacia abajo. Durante el movimiento de la | |||
placa el muelle permanece siempre estirado. | |||
#¿Qué valor debe tener <math>k</math> para que la posición inicial sea una posición de equilibrio? Encuentra la reducción vincular en <math>A</math> para la situación de equilibrio. | |||
#Determina la reducción cinemática del movimiento {21} en el punto <math>G</math> de la placa, así como su derivada temporal. | |||
#Una pequeña perturbación hace que la placa empiece a girar con velocidad angular inicial <math>\dot{\theta}(0)=\omega_0</math>. Encuentra la expresión de la energía cinética de la placa durante su movimiento (ver Nota). | |||
#Encuentra una integral primera del movimiento. Supón que el valor de <math>k</math> corresponde a la condición de equilibrio del apartado 1. | |||
#Considerando el valor de <math>k</math> del apartado anterior, discute razonadamente la estabilidad del equilibrio del apartado 1. | |||
< | '''Nota:''' El momento de inercia de una placa homogénea cuadrada de masa <math>M</math> y lado <math>l</math>, respecto a un eje perpendicular a ella que pasa por su centro es <math>Ml^2/6</math>. | ||
< | ==[[Barra con centro deslizando sobre eje, Septiembre 2016 (MR G.I.C.)|Barra con centro deslizando sobre eje ]] == | ||
[[Imagen:MR_barra_centro_eje_enunciado.png|right]] | |||
Una barra homogénea delgada (sólido "2") de masa <math>M</math> y longitud <math>2L</math> se mueve de modo que | |||
su centro se encuentra siempre sobre el eje <math>OZ_1</math>. La barra tiene dos grados de libertad de rotación. | |||
El sistema auxiliar <math>OX_0Y_0Z_0</math> se define de modo que la barra esté siempre contenida | |||
en el plano <math>OX_0Z_0</math>. La barra está sometida a la acción de la gravedad, como se indica en | |||
la figura. El contacto de la barra con el eje <math>OZ_1</math> es liso. | |||
#Calcula las reducciones cinematicas en el centro de la barra de los tres movimientos que se pueden definir en el problema. | |||
#Encuentra la expresión del momento cinético de la barra respecto de su centro. | |||
#Encuentra la expresión de la energía cinética de la barra. | |||
#Escribe la Lagrangiana del sistema, así como una integral primera que no sea la energía mecánica. | |||
#En el instante inicial, el centro de la barra se encuentra en el punto <math>O</math> y los valores iniciales de las coordenadas angulares son <math>\theta(0) = \pi/2</math> y <math>\phi(0)=0</math>. La barra se encuentra en reposo. Se ejerce una percusión <math>\hat{\vec{F}} = \hat{F}_0\,(\vec{\jmath}_0 + \vec{k}_0)</math> aplicada en el punto <math>B</math>. Determina los valores de las velocidades generalizadas justo después de la percusión. | |||
y | |||
Revisión del 16:39 28 nov 2023
Problemas del boeltín
Engranaje sobre cremallera
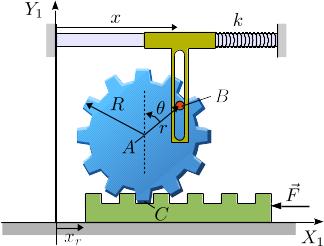
La figura muestra un sistema mecánico formado por un engranaje que rueda sobre una cremallera y está conectado a un deslizador con una ranura que desliza respecto al pasador en . El deslizador está acoplado a un muelle, de constante elástica , que se encuentra relajado cuando . En ese instante se tiene . Las masas del engranaje, el deslizador y la cremallera son la misma e igual a . El radio de giro del engranaje es . El contacto entre el pasador y la ranura es liso. El mecanismo es accionado por una fuerza aplicada sobe la cremallera como se indica en la figura.
- Encuentra el número de grados de libertad y elige un conjunto de coordenadas generalizadas para describir el movimiento.
- Encuentra las ecuaciones diferenciales del movimiento.
Triciclo
Dos partículas unidas por una barra sin masa con una cuchilla
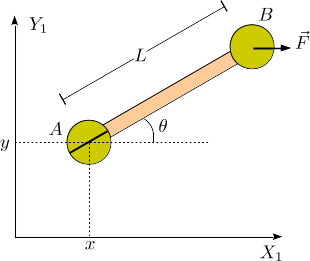
Dos partículas puntuales de masa están unidas por una barra de longitud y masa despreciable. Las partículas deslizan sobre un plano fijo , pero una de las partículas tiene una cuchilla, de modo que su velocidad sólo puede tener componente paralela a la cuchilla. Una fuerza constante actúa sobre la partícula que no tiene la cuchilla.
- Encuentra la expresión del vínculo no holónomo del sistema.
- Escribe las ecuaciones de Lagrange utilizando la técnica de los multiplicadores de Lagrange.
- Identifica el significado físico del multiplicador de Lagrange.
Otros problemas
Deslizadera y disco rodando sin deslizar
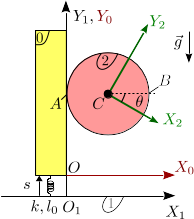
Un disco homogéneo (sólido "2") de masa y radio puede rotar alrededor de su centro , que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa puede moverse a lo largo del eje , de modo que en el punto de contacto el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un muelle de constante elástica y longitud natural . El otro extremo del muelle está anclado en un punto fijo del eje , de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura.
- ¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales.
- Calcula las energías cinética y potencial del sistema en función de sus grados de libertad.
- Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento.
- Se aplica sobre el disco un par de fuerzas externo . Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de aparece una resonancia mecánica?
- Ahora no hay par aplicado. Se aplica una percusión sobre el punto del sólido "2". En el instante de la percusión se cumple , , , . Calcula el estado del sistema inmediatamente después de la percusión.
Aro colgando de una barra que rota
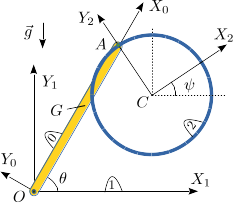
La barra homogénea (sólido "0") tiene masa y longitud . Está articulada en el punto fijo y rota de modo que está siempre contenida en el plano . En su extremo está articulado un aro homogéneo de radio y masa (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos como coordenadas para resolver el problema.
- Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}.
- Calcula las energías cinética y potencial totales del sistema.
- Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento.
- Se impone el vínculo cinemático . Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene , .
- Supongamos que las coordenadas son de nuevo libres. Supón que se tiene , . En ese instante una percusión actúa sobre el punto . Determina el estado cinemático del sistema justo después de la percusión.
Barra rotando alrededor de barra horizontal con muelle
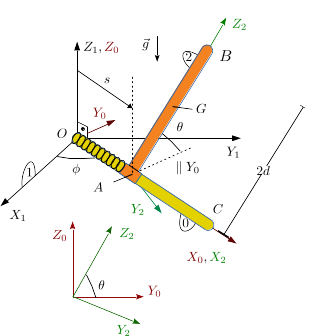
Una barra de longitud y masa despreciable (sólido "0") puede rotar alrededor del eje . El punto de la barra es fijo. La barra "0" siempre está contenida en el plano . Otra barra, también de longitud y masa (sólido "2"), está conectada a la barra "0" por un pasador en el punto . El pasador desliza sobre la barra "0". Además, la barra "2" gira alrededor de la barra "0". Un muelle de constante elástica y longitud natural nula conecta los puntos y .
- Determina las reducciones cinemáticas y en .
- Calcula el momento cinético de la barra "2" respecto de .
- A partir de ahora suponemos que , es decir, la coordenada ya no es un grado de libertad. Escribe las ecuaciones de Lagrange del sistema.
- En tenemos , , y ( sigue estando fijada). La barra "2" recibe una percusión en el punto B. Determina el estado del sistema justo después de la percusión.
Disco rodando sobre plataforma con muelle
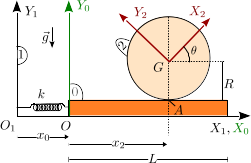
Un disco de masa y radio (sólido "2") rueda sin deslizar sobre una placa rectangular de masa (sólido "0"). La placa desliza sin rozamiento sobre el eje fijo . Un muelle de constante elástica y longitud natural nula conecta la placa con el eje .
- Encuentra la reducción cinemática del movimiento absoluto.
- Escribe la Lagrangiana del sistema.
- Escribe las ecuaciones de Lagrange.
- En el estado inicial los dos sólidos están en reposo y , . Se somete la placa a una percusión aplicada en su extremo izquierdo. ¿Cuánto valen las velocidades generalizadas inmediatamente después de la percusión? ¿Cuál es la frecuencia de las oscilaciones de la placa en el movimiento después de la percusión?
Disco rodando en cavidad con muelle de torsión
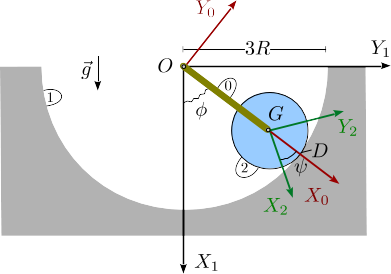
Un disco de radio y masa (sólido "2") rueda sin deslizar sobre una superficie circular cóncava (sólido "1") de radio . En el centro del disco se articula una barra (sólido "0") de masa despreciable y longitud . El otro extremo de la barra se articula en un punto fijo . La barra está conectada a su vez a un resorte de torsión en el punto . Este resorte ejerce un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él se puede expresar como , siendo una constante.
- Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre y ?.
- Calcula la energía cinética del disco y su energía potencial.
- Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación.
- Estando el disco en reposo y con , se aplica al centro del disco una percusión . Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje.
Barra con muelle horizontal
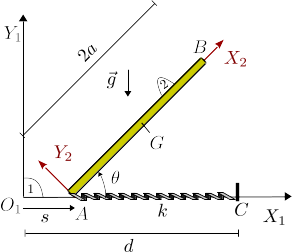
Una barra de longitud y masa (sólido "2") desliza con un extremo (punto ) apoyado sobre un plano horizontal liso. El extremo está unido a un muelle de constante elástica k y longitud natural nula anclado en que se mantiene siempre horizontal. La gravedad actúa verticalmente hacia abajo. En la barra estaba en reposo, el punto coincidía con y la barra estaba completamente vertical.
- Encuentra la expresión que da la cantidad de movimiento de la barra.
- Encuentra la expresión que da el momento cinético de la barra respecto del punto .
- Determina las ecuaciones de movimiento del sistema.
- ¿Cómo es la fuerza de ligadura en el punto ?
- Supongamos que se fuerza al punto a moverse con velocidad uniforme . ¿Cual de estas fuerzas aplicadas en consigue ese efecto?
Placa cuadrada pivotando con muelle
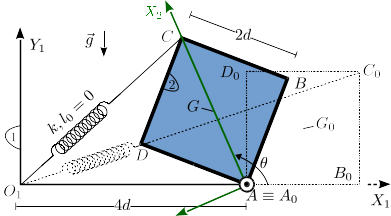
El sólido "2' es una placa cuadrada y homogénea, de lado y masa . La placa está articulada en su vértice , que permanece fijo. El vértice de la placa está conectado a un muelle de constante elástica y longitud natural nula, anclado en el punto . En el instante inicial la posición de la placa está indicada en la figura por el cuadrado punteado. En esa posición inicial, el lado no está apoyado en ninguna superficie. La gravedad actúa en la dirección vertical hacia abajo. Durante el movimiento de la placa el muelle permanece siempre estirado.
- ¿Qué valor debe tener para que la posición inicial sea una posición de equilibrio? Encuentra la reducción vincular en para la situación de equilibrio.
- Determina la reducción cinemática del movimiento {21} en el punto de la placa, así como su derivada temporal.
- Una pequeña perturbación hace que la placa empiece a girar con velocidad angular inicial . Encuentra la expresión de la energía cinética de la placa durante su movimiento (ver Nota).
- Encuentra una integral primera del movimiento. Supón que el valor de corresponde a la condición de equilibrio del apartado 1.
- Considerando el valor de del apartado anterior, discute razonadamente la estabilidad del equilibrio del apartado 1.
Nota: El momento de inercia de una placa homogénea cuadrada de masa y lado , respecto a un eje perpendicular a ella que pasa por su centro es .
Barra con centro deslizando sobre eje
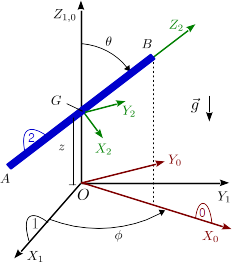
Una barra homogénea delgada (sólido "2") de masa y longitud se mueve de modo que su centro se encuentra siempre sobre el eje . La barra tiene dos grados de libertad de rotación. El sistema auxiliar se define de modo que la barra esté siempre contenida en el plano . La barra está sometida a la acción de la gravedad, como se indica en la figura. El contacto de la barra con el eje es liso.
- Calcula las reducciones cinematicas en el centro de la barra de los tres movimientos que se pueden definir en el problema.
- Encuentra la expresión del momento cinético de la barra respecto de su centro.
- Encuentra la expresión de la energía cinética de la barra.
- Escribe la Lagrangiana del sistema, así como una integral primera que no sea la energía mecánica.
- En el instante inicial, el centro de la barra se encuentra en el punto y los valores iniciales de las coordenadas angulares son y . La barra se encuentra en reposo. Se ejerce una percusión aplicada en el punto . Determina los valores de las velocidades generalizadas justo después de la percusión.

















![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},{\hat {F}}_{0},0]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45be34e4e576e91e7146a6c511e29b15fa8bb600)






















![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},0,{\hat {F}}_{0}]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4a23b503f604c1368ebbf85e321e420e2f0f41)























