Diferencia entre las páginas «Archivo:Percusion-tres-masas-percusiones.png» y «Esfera en recipiente cilíndrico»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | |||
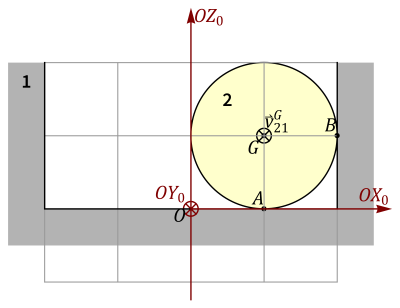
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante <math>v_0</math> alrededor del eje vertical. | |||
Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje <math>{OZ}_1</math>=OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano <math>{OX}_0Z_0</math> . Con ayuda de este sistema determine y exprese: | |||
# Las velocidades angulares <math>\vec{\omega}_{01}</math>, <math>\vec{\omega}_{21}</math> y <math>\vec{\omega}_{20}</math> | |||
# La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura) | |||
# Las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math> | |||
# Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1. | |||
<center>[[Archivo:Esfera-recipiente-cilindrico.png|400px]]</center> | |||
==Velocidades angulares== | |||
===Arrastre, {01}=== | |||
El movimiento del sistema “0&” respecto al 1 es una rotación alrededor del eje <math>OZ_1=OZ_0</math>. La velocidad angular es de la forma | |||
<center><math>\vec{\omega}_{01}=\omega_{01}\vec{k}_0</math></center> | |||
El valor lo obtenemos de que conocemos la velocidad de G | |||
<center><math>\vec{v}^G_{01}=\vec{\omega}_{01}\times\overrightarrow{OG}</math></center> | |||
La posición de G en el sistema 0 es, en todo momento, | |||
<center><math>\overrightarrow{OG}=R\vec{\imath}_0+R\vec{k}_0</math></center> | |||
Por ello, G es un punto fijo en el movimiento relativo. | |||
<center><math>\vec{v}^G_{21}=\overbrace{\vec{v}^G_{20}}^{=\vec{0}}+\vec{v}^G_{01}</math></center> | |||
por lo que | |||
<center><math>\vec{v}^G_{01}= v_0\vec{\jmath}_0</math></center> | |||
Esto nos da | |||
<center><math>v_0\vec{\jmath}_0 = \left(\omega_{01}\vec{k}_0\right)\times \left(R\vec{\imath}_0+R\vec{k}_0\right) = \omega_{01}R\vec{\jmath}_0</math></center> | |||
y | |||
<center><math>\omega_{01}=\dfrac{v_0}{R}\qquad\qquad \vec{\omega}_{01}=\frac{v_0}{R}\vec{k}_0</math></center> | |||
===Absoluta, {21}=== | |||
Para la absoluta operamos de manera similar. En este caso observamos que puesto que en el punto A y en el B no hay deslizamiento | |||
<center><math>\vec{v}^A_{21}=\vec{v}^B_{21}=\vec{0}</math></center> | |||
y, por tanto, el EIR debe pasar por esos dos puntos. La velocidad angular es entonces de la forma | |||
<center><math>\vec{\omega}_{21}=\Omega\left(\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
Aplicamos ahora que | |||
<center><math>v_0\vec{\jmath}_0=\vec{v}^G_{21}=\vec{\omega}_{21}\times\overrightarrow{AG}=\Omega\left(\vec{\imath}_0+\vec{k}_0\right)\times \left(R\vec{k}_0\right)=-\Omega R\vec{\jmath}_0</math></center> | |||
De donde | |||
<center><math>\Omega=-\frac{v_0}{R}\qquad\qquad \vec{\omega}_{21}=-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
===Relativa, {20}=== | |||
Una vez que tenemos la absoluta y la de arrastre, la relativa es inmediata | |||
<center><math>\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\qquad\Rightarrow\qquad \vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}</math></center> | |||
lo que da | |||
<center><math>\vec{\omega}_{20}=-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right) - \frac{v_0}{R}\vec{k}_0 = -\frac{v_0}{R}\left(\vec{\imath}_0+2\vec{k}_0\right)</math></center> | |||
==Ejes instantáneos de rotación== | |||
* El EIR de arrastre {01} pasa por el origen y lleva la dirección de <math>OZ_0</math>. | |||
* El EIR absoluto {21} pasa por los puntos A y B. | |||
* El EIR relativo {20} pasa por G (punto fijo en el movimiento {20}) y lleva la dirección de <center><math>\left(\vec{\imath}_0+2\vec{k}_0\right)</math></center>. | |||
Los tres ejes se cortan en el punto <math>Q(0,-R)</math> que es un punto fijo en los tres movimientos. | |||
==Aceleraciones angulares== | |||
Las aceleraciones angulares de arrastre y relativa son nulas, por ser constantes las velocidades angulares en ambos movimientos | |||
<center><math>\vec{\omega}_{01}=\frac{v_0}{R}\vec{k}_1\qquad\qquad\vec{\omega}_{20}=-\frac{v_0}{R}\left(\vec{\imath}_0+2\vec{k}_0\right)</math></center> | |||
<center><math>\vec{\alpha}_{01}=\vec{\alpha}_{20}=\vec{0}</math></center> | |||
La velocidad angular absoluta {21} no es constante, aunque lo parezca | |||
<center><math>\vec{\omega}_{21}=-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
ya que los vectores de la base 0 son dependientes del tiempo en el sistema 1. | |||
Aplicamos la ley de composición de velocidades angulares | |||
<center><math>\vec{\alpha}_{21}=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}+\vec{\omega}_{20}</math></center> | |||
lo que nos da | |||
<center><math>\vec{\alpha}_{21}= \left(\frac{v_0}{R}\vec{k}_0\right)\times \left(-\frac{v_0}{R}\left(\vec{\imath}_0+2\vec{k}_0\right)\right)= | |||
-\frac{v_0^2}{R^2}\vec{\jmath}_0</math></center> | |||
==Aceleraciones lineales== | |||
Para las aceleraciones lineales tenemos la fórmula general | |||
<center><math>\vec{a}^P_{21} = \vec{a}^O_{21}+\vec{\alpha}_{21}\times\overrightarrow{OP}+\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{OP}\right)</math></center> | |||
pero en este caso el punto O no es un buen punto de referencia, ya que también posee aceleración y desconocemos cuál es (se puede calcular). Deberíamos usar el punto Q, donde se cortan los ejes, como punto de referencia, ya que este punto tiene aceleración nula. | |||
Si no hemos observado que Q es el punto fijo podemos hacerlo de otra forma. Primero calculamos la aceleración de G observando que es un punto fijo en el movimiento {20} | |||
<center><math>\vec{a}^G_{21}=\overbrace{\vec{a}^G_{20}}^{=\vec{0}}+\vec{a}^G_{01}+2\vec{\omega}_{01}\times\overbrace{\vec{v}^G_{20}}^{=\vec{0}}=\vec{a}^G_{01}</math></center> | |||
luego su aceleración es la que tiene en el movimiento de arrastre, que es simplemente la de un movimiento circular alrededor de <math>OZ_0</math> | |||
<center><math>\vec{a}^G_{01} = \overbrace{\vec{a}^O_{01}}^{=\vec{0}}+\overbrace{\vec{\alpha}_{01}}^{=\vec{0}}\times\overrightarrow{OG}+\vec{\omega}_{01}\times\left(\vec{\omega}_{01}\times\overrightarrow{OG}\right)=-\frac{v_0^2}{R}\vec{\imath}_0</math></center> | |||
y una vez que tenemos esta hallamos la de los otros dos puntos | |||
<center><math>\vec{a}^A_{21} = \vec{a}^G_{21}+\vec{\alpha}_{21}\times\overrightarrow{GA}+\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{GA}\right)</math></center> | |||
donde los tres términos valen | |||
<center><math>\vec{a}^G_{21}=-\frac{v_0^2}{R}\vec{\imath}_0</math></center> | |||
<center><math>\vec{\alpha}_{21}\times\overrightarrow{GA}=\left(-\frac{v_0^2}{R^2}\vec{\jmath}_0\right)\times \left(-R\vec{k}_0\right)=\frac{v_0^2}{R}\vec{\imath}_0</math></center> | |||
<center><math>\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{GA}\right)=\left(-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)\right)\times\left(\left(-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)\right)\times\left(-R\vec{k}_0\right)\right)=\frac{v_0^2}{R}\left(-\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
Sumando los tres términos resulta | |||
<center><math>\vec{a}^A_{21}=\frac{v_0^2}{R}\left(-\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
operamos igualmente para el punto B | |||
<center><math>\vec{\alpha}_{21}\times\overrightarrow{GB}=\left(-\frac{v_0^2}{R^2}\vec{\jmath}_0\right)\times \left(R\vec{\imath}_0\right)=\frac{v_0^2}{R}\vec{k}_0</math></center> | |||
<center><math>\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{GB}\right)=\left(-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)\right)\times\left(\left(-\frac{v_0}{R}\left(\vec{\imath}_0+\vec{k}_0\right)\right)\times\left(R\vec{\imath}_0\right)\right)=\frac{v_0^2}{R}\left(-\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
y resulta | |||
<center><math>\vec{a}^A_{21}=\frac{2v_0^2}{R}\left(-\vec{\imath}_0+\vec{k}_0\right)</math></center> | |||
Revisión del 14:46 28 nov 2023
Enunciado
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante alrededor del eje vertical. Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje =OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano . Con ayuda de este sistema determine y exprese:
- Las velocidades angulares , y
- La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura)
- Las aceleraciones angulares , y
- Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1.
Velocidades angulares
Arrastre, {01}
El movimiento del sistema “0&” respecto al 1 es una rotación alrededor del eje . La velocidad angular es de la forma
El valor lo obtenemos de que conocemos la velocidad de G
La posición de G en el sistema 0 es, en todo momento,
Por ello, G es un punto fijo en el movimiento relativo.
por lo que
Esto nos da
y
Absoluta, {21}
Para la absoluta operamos de manera similar. En este caso observamos que puesto que en el punto A y en el B no hay deslizamiento
y, por tanto, el EIR debe pasar por esos dos puntos. La velocidad angular es entonces de la forma
Aplicamos ahora que
De donde
Relativa, {20}
Una vez que tenemos la absoluta y la de arrastre, la relativa es inmediata
lo que da
Ejes instantáneos de rotación
- El EIR de arrastre {01} pasa por el origen y lleva la dirección de .
- El EIR absoluto {21} pasa por los puntos A y B.
- El EIR relativo {20} pasa por G (punto fijo en el movimiento {20}) y lleva la dirección de
.
Los tres ejes se cortan en el punto que es un punto fijo en los tres movimientos.
Aceleraciones angulares
Las aceleraciones angulares de arrastre y relativa son nulas, por ser constantes las velocidades angulares en ambos movimientos
La velocidad angular absoluta {21} no es constante, aunque lo parezca
ya que los vectores de la base 0 son dependientes del tiempo en el sistema 1.
Aplicamos la ley de composición de velocidades angulares
lo que nos da
Aceleraciones lineales
Para las aceleraciones lineales tenemos la fórmula general
pero en este caso el punto O no es un buen punto de referencia, ya que también posee aceleración y desconocemos cuál es (se puede calcular). Deberíamos usar el punto Q, donde se cortan los ejes, como punto de referencia, ya que este punto tiene aceleración nula.
Si no hemos observado que Q es el punto fijo podemos hacerlo de otra forma. Primero calculamos la aceleración de G observando que es un punto fijo en el movimiento {20}
luego su aceleración es la que tiene en el movimiento de arrastre, que es simplemente la de un movimiento circular alrededor de
y una vez que tenemos esta hallamos la de los otros dos puntos
donde los tres términos valen
Sumando los tres términos resulta
operamos igualmente para el punto B
y resulta
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 17:19 27 nov 2023 | 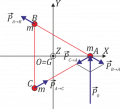 | 400 × 364 (39 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:









































