Ecuaciones de movimiento de un péndulo usando el teorema del momento cinético (GIC)

Enunciado

Encuentra las ecuaciones que describen el móvimiento de un péndulo ideal utilizando la variación del momento angular.

Solución

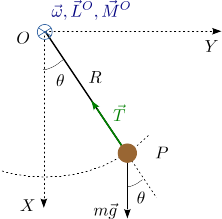
La figura de la derecha muestra un péndulo formado por una masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m } colgando de un hilo sin masa e inextensible de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R } . La trayectoria que describe la masa es una circunferencia de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R } y con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } , punto del que cuelga la cuerda.

La masa está sometida a la acción de su peso y la tensión que ejerce la cuerda. Vamos a resolver el problema usando el momento angular de la masa y su derivada. El vector de posición de la partícula es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{r} = \overrightarrow{OP} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath} }

El movimiento circular que describe la partícula puede describirse con un vector rotación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega} } de la forma

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega} = \dot{\theta}\,\vec{k} }

La velocidad de la partícula es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v} = \vec{\omega}\times\vec{r} = R\dot{\theta}\,(-\mathrm{sen}\theta\,\vec{\imath} + \cos\theta\,\vec{\jmath}) }

Esto también puede obtenerse derivando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{r} } respecto del tiempo.

El movimiento circular de la partícula puede entenderse como una rotación alrededor del eje fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OZ } . Entonces, el momento de inercia de la partícula respecto de ese eje es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I = mR^2 }

Y el momento angular respecto de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}^O = I\vec{\omega} = I\dot{\theta}\,\vec{k} }

La variación en el tiempo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}^O } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}\vec{L}^O}{\mathrm{d}t} = \vec{M}^O \Longrightarrow I\dot{\vec{\omega}} = \vec{M}^O }

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}^O } es el momento neto de las fuerzas que actúan sobre la partícula respecto del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } . En este caso las fuerzas son el peso y la tensión de la cuerda, es decir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}^O = \overrightarrow{OP}\times(m\vec{g}) + \overrightarrow{OP}\times\vec{T} }

El momento de la tensión de la cuerda es cero, pues Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OP} } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{T} } son paralelos. Para el peso tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OP}\times(m\vec{g}) = (R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}) \times (mg\,\vec{\imath}) = -mgR\,\mathrm{sen}\,\theta\,\vec{k} }

Tenemos entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I\dot{\vec{\omega}} = I\ddot{\theta}\,\vec{k} = -mgR\,\mathrm{sen}\,\theta\,\vec{k} }

Por tanto, la ecuación diferencial para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta(t) } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{\theta} = -\dfrac{mgR}{I}\,\mathrm{sen}\,\theta }

Teniendo en cuenta la expresión para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I } obtenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{\theta} = -\dfrac{g}{R}\,\mathrm{sen}\,\theta }

que es la misma ecuación que obteníamos en el tema de dinámica de la partícula. Esta ecuación no la sabemos resolver, pero cuando el ángulo es pequeño podemos hacer la aproximación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\,\theta \approx\theta } y nos queda la ecuación de un oscilador armónico con frecuencia angular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega = \sqrt{g/R} } .