Diferencia entre las páginas «Archivo:MRGIC barra esquina CIR.png» y «Cono rotando con punto fijo (Nov. 2018)»
Sin resumen de edición |
(Página creada con «= Enunciado = right Un cono con ángulo de abertura <math>\pi/4</math> y radio de la base <math>R</math> se mueve de modo que rueda sin deslizar sobre el plano fijo "1" y su vértice <math>C</math> permanece fijo sobre el eje <math>OZ_1</math>. La base del cono permanece siempre perpendicular al plano <math>OX_1Y_1</math>. El sólido auxiliar "0" se escoge de modo que el plano <math>X_0Z_0</math> contiene siempre a los puntos…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[File:MRGIC_cono_rotando_enunciado.png|right]] | |||
Un cono con ángulo de abertura <math>\pi/4</math> y radio de la base <math>R</math> se mueve de modo | |||
que rueda sin deslizar sobre el plano fijo "1" y su vértice <math>C</math> permanece fijo | |||
sobre el eje <math>OZ_1</math>. La base del cono permanece siempre perpendicular al plano <math>OX_1Y_1</math>. El sólido auxiliar "0" se escoge de modo que el plano | |||
<math>X_0Z_0</math> contiene siempre a los puntos <math>A</math>, <math>B</math> y <math>C</math> del cono. El sólido "0" | |||
rota alrededor del eje <math>OZ_1</math> con velocidad angular constante <math>\vec{\Omega} = | |||
\Omega\,\vec{k}_{0,1}</math>. | |||
#Localiza y dibuja los ejes de rotación de los movimientos {01}, {20} y {21}. ¿Qué tipo de eje es cada uno de ellos? | |||
#Calcula las reducciones cinemáticas en <math>G</math> de los tres movimientos relativos. | |||
#Calcula las derivadas temporales de las reducciones cinemáticas en <math>G</math> de los tres movimientos relativos. | |||
= Solución = | |||
== Análisis del enunciado == | |||
De los datos del enunciado podemos deducir los siguientes hechos: | |||
#El cono rueda sin desliar sobre el plano, por tanto <math>\vec{v}^{\,A}_{21}=\vec{0}</math>. | |||
#El punto <math>C</math> es fijo sobre el eje <math>OZ_1</math>. Entonces <math>\vec{v}^{\,C}_{21}=\vec{0}</math>. | |||
#Del dibujo vemos que el movimiento {01} es un par de revolución con <math>\vec{v}^{\,O}_{01}=\vec{0}</math> y <math>\vec{\omega}_{01}=\Omega\,\vec{k}_{0,1}</math>. | |||
#También relacionado con este movimiento vemos que el centro de la base del cono no se mueve respecto al plano <math>OX_0Z_0</math>, por lo que <math>\vec{v}^{\,G}_{20}=\vec{0}</math>. | |||
== Ejes de los movimientos == | |||
[[File:MRGIC_cono_rotando_ejes.png|right]] | |||
La figura de la derecha muestra la localización de los ejes. Son | |||
Como <math>\vec{v}^{\,O}_{01}=\vec{0}</math> y <math>\vec{\omega}_{01}=\Omega\,\vec{\omega}_{01}</math>, el eje del movimiento {01} es <math> \Delta^{EPR}_{01}\equiv OZ_1</math>. Es un eje permanente de rotación. | |||
Como <math>\vec{v}^{\,A}_{21}=\vec{v}^{\,A}_{21}=\vec{0}</math> tenemos <math>\Delta^{EIR}_{21}\equiv CA</math>. Es un eje instantáneo de rotación. | |||
Por último, con la composición {21}={20} + {01}. Aplicándola en <math>C</math> tenemos | |||
<center><math> | |||
\vec{v}^{\,C}_{21}=\vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} | |||
\Longrightarrow | |||
\vec{v}^{\,C}_{20}=\vec{v}^{\,C}_{21} - \vec{v}^{\,C}_{01} = \vec{0} | |||
</math></center> | |||
Además, <math>\vec{v}^{\,G}_{20}</math>, por lo que el eje del movimiento {20} es <math>\Delta^{EPR}_{20}</math> es un eje permanente de rotación. | |||
== Reducciones cinemáticas == | |||
'''Movimiento {01}''' | |||
En el análisis previo ya hemos obtenido la reducción cinemática de este movimiento | |||
<center><math> | |||
\vec{\omega}_{01}=\Omega\,\vec{k}_{0,1}, | |||
\qquad | |||
\vec{v}^{\,O}_{01} = \vec{0}. | |||
</math></center> | |||
'''Movimiento {20}''' | |||
Del análisis de los ejes tenemos | |||
<center><math> | |||
\vec{\omega}_{20}=\omega_{20}\,\vec{\imath}_{0}, | |||
\qquad | |||
\vec{v}^{\,G}_{20} = \vec{0}. | |||
</math></center> | |||
'''Movimiento {21}''' | |||
Usando la composición {21} = {20} + {01} obtenemos | |||
<center><math> | |||
\begin{array}{l} | |||
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = | |||
\omega_{20}\,\vec{\imath}_0 + \Omega\,\vec{k}_0.\\ | |||
\\ | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01}= | |||
\vec{v}^{\,G}_{01} | |||
\end{array} | |||
</math></center> | |||
Para calcular esta velocidad usamos la ecuación del campo de velocidades del movimiento {01} | |||
<center><math> | |||
\vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG} = | |||
(\Omega\,\vec{k}_0)\times(R\,\vec{\imath}_0+R\,\vec{k}_0) = R\Omega\,\vec{\jmath}_0. | |||
</math></center> | |||
Por otro lado sabemos que <math>\vec{v}^{\,A}_{21}=\vec{0}</math>. Usando la ecuación del campo de velocidades del movimiento {21} obtenemos | |||
<center><math> | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG} = | |||
(\omega_{20}\,\vec{\imath}_0)\times(R\,\vec{k}_0) = -R\omega_{20}\,\vec{\jmath}_0. | |||
</math></center> | |||
Comparando los dos valores obtenemos <math>\omega_{20} = -\Omega</math>. | |||
Con esto tenemos las tres reducciones cinemáticas | |||
<center><math> | |||
\begin{array}{ll} | |||
\vec{\omega}_{01} = \Omega\,\vec{k}_0, & \vec{v}^{\,G}_{01}=R\Omega\,\vec{\jmath}_0,\\ | |||
\\ | |||
\vec{\omega}_{20} = -\Omega\,\vec{\imath}_0, & \vec{v}^{\,G}_{20}=\vec{0},\\ | |||
\\ | |||
\vec{\omega}_{21} = \Omega\,(-\vec{\imath}_0 + \vec{k}_0), & \vec{v}^{\,G}_{21}=R\Omega\,\vec{\jmath}_0. | |||
\end{array} | |||
</math></center> | |||
== Derivadas temporales de la reducciones cinemáticas == | |||
'''Movimiento {01}''': al ser una rotación de eje permanente tenemos | |||
<center><math> | |||
\begin{array}{l} | |||
\vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1= | |||
\vec{0},\\ | |||
\\ | |||
\vec{a}^{\,O}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O}_{01}}{\mathrm{d}t}\right|_1= | |||
\vec{0}. | |||
\end{array} | |||
</math></center> | |||
Usamos la ecuación del campo de aceleraciones del movimiento {01} para calcular la aceleración en <math>G</math> | |||
<center><math> | |||
\vec{a}^{\,G}_{01} = \vec{a}^{\,O}_{01} + \vec{\alpha}_{01}\times\overrightarrow{OG} + \vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OG}) = -R\Omega^2\vec{\imath}_{0}. | |||
</math></center> | |||
'''Movimiento {20}''': también es una rotación de eje permanente, por lo que | |||
<center><math> | |||
\begin{array}{l} | |||
\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0= | |||
\vec{0},\\ | |||
\\ | |||
\vec{a}^{\,G}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,G}_{20}}{\mathrm{d}t}\right|_0= | |||
\vec{0}. | |||
\end{array} | |||
</math></center> | |||
'''Movimiento {21} ''' | |||
Utilizamos las leyes de composición | |||
<center><math> | |||
\begin{array}{l} | |||
\vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} = -\Omega^2\,\vec{\jmath}_0,\\ | |||
\\ | |||
\vec{a}^{\,G}_{21} = \vec{a}^{\,G}_{20} + \vec{a}^{\,G}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,G}_{20} = -R\Omega^2\,\vec{\imath}_0. | |||
\end{array} | |||
</math></center> | |||
[[Categoría:Problemas de cinética del sólido rígido]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión actual - 12:52 8 nov 2023
Enunciado
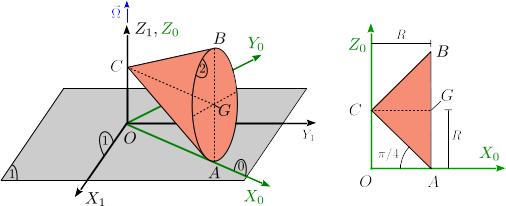
Un cono con ángulo de abertura y radio de la base se mueve de modo que rueda sin deslizar sobre el plano fijo "1" y su vértice permanece fijo sobre el eje . La base del cono permanece siempre perpendicular al plano . El sólido auxiliar "0" se escoge de modo que el plano contiene siempre a los puntos , y del cono. El sólido "0" rota alrededor del eje con velocidad angular constante .
- Localiza y dibuja los ejes de rotación de los movimientos {01}, {20} y {21}. ¿Qué tipo de eje es cada uno de ellos?
- Calcula las reducciones cinemáticas en de los tres movimientos relativos.
- Calcula las derivadas temporales de las reducciones cinemáticas en de los tres movimientos relativos.
Solución
Análisis del enunciado
De los datos del enunciado podemos deducir los siguientes hechos:
- El cono rueda sin desliar sobre el plano, por tanto .
- El punto es fijo sobre el eje . Entonces .
- Del dibujo vemos que el movimiento {01} es un par de revolución con y .
- También relacionado con este movimiento vemos que el centro de la base del cono no se mueve respecto al plano , por lo que .
Ejes de los movimientos
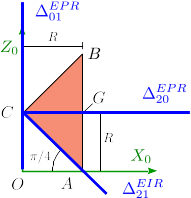
La figura de la derecha muestra la localización de los ejes. Son Como y , el eje del movimiento {01} es . Es un eje permanente de rotación.
Como tenemos . Es un eje instantáneo de rotación.
Por último, con la composición {21}={20} + {01}. Aplicándola en tenemos
Además, , por lo que el eje del movimiento {20} es es un eje permanente de rotación.
Reducciones cinemáticas
Movimiento {01} En el análisis previo ya hemos obtenido la reducción cinemática de este movimiento
Movimiento {20} Del análisis de los ejes tenemos
Movimiento {21} Usando la composición {21} = {20} + {01} obtenemos
Para calcular esta velocidad usamos la ecuación del campo de velocidades del movimiento {01}
Por otro lado sabemos que . Usando la ecuación del campo de velocidades del movimiento {21} obtenemos
Comparando los dos valores obtenemos .
Con esto tenemos las tres reducciones cinemáticas
Derivadas temporales de la reducciones cinemáticas
Movimiento {01}: al ser una rotación de eje permanente tenemos
Usamos la ecuación del campo de aceleraciones del movimiento {01} para calcular la aceleración en
Movimiento {20}: también es una rotación de eje permanente, por lo que
Movimiento {21} Utilizamos las leyes de composición
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 12:52 8 nov 2023 |  | 311 × 277 (30 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
La siguiente página usa este archivo:

































