La versión para imprimir ya no se admite y puede contener errores de representación. Actualiza los marcadores del navegador y utiliza en su lugar la función de impresión predeterminada del navegador.
Enunciado
La escuadra  (sólido “2”) se mueve respecto a la escuadra
(sólido “2”) se mueve respecto a la escuadra  (sólido “1”) de forma que su origen de coordenadas,
(sólido “1”) de forma que su origen de coordenadas,  , verifica la ecuación paramétrica
, verifica la ecuación paramétrica

siendo  el ángulo que el eje
el ángulo que el eje  forma con el
forma con el  .
.
- Calcule la velocidad instantánea del punto
 en el movimiento {21}:
en el movimiento {21}:  .
.
- Determine la posición del CIR
 y exprésela empleando el sistema de referencia ligado al sólido “1”.
y exprésela empleando el sistema de referencia ligado al sólido “1”.
- Exprese la posición del mismo punto
 en el sistema de referencia ligado al sólido “2”.
en el sistema de referencia ligado al sólido “2”.
Velocidad
La velocidad del punto  , como parte del sólido “2” respecto al “1”,
, como parte del sólido “2” respecto al “1”,  , puede calcularse de diferentes formas.
, puede calcularse de diferentes formas.
Empleando el sistema de referencia “1”
Debemos hallar la velocidad de un punto cuya posición no conocemos en todo instante. El punto cuya posición sí conocemos y podemos derivar es  . Por ello, debemos usar la expresión del campo de velocidades
. Por ello, debemos usar la expresión del campo de velocidades

Veamos cada término por separado.
La velocidad de  en el movimiento {21} sí puede hallarse derivando respecto al tiempo, por aplicación de la regla de la cadena.
en el movimiento {21} sí puede hallarse derivando respecto al tiempo, por aplicación de la regla de la cadena.

La velocidad angular es inmediata, puesto que conocemos el ángulo que forman los ejes  y
y 

El vector de posición relativo es el opuesto al que aparece en el enunciado

Reuniendo todo esto obtenemos la velocidad del punto 

Empleando el sistema de referencia “2”
Puesto que el punto  es el origen de coordenadas del sistema de referencia “1”, puede parecer más intuitivo considerar el movimiento inverso, del sólido “1” respecto al “2”. Las velocidades de los movimientos inversos se relacionan por la igualdad
es el origen de coordenadas del sistema de referencia “1”, puede parecer más intuitivo considerar el movimiento inverso, del sólido “1” respecto al “2”. Las velocidades de los movimientos inversos se relacionan por la igualdad

Para hallar el segundo miembro, expresaremos la posición del punto  en el sistema de referencia ligado al sólido “2”. El vector de posición relativo es, según dijimos,
en el sistema de referencia ligado al sólido “2”. El vector de posición relativo es, según dijimos,

Esta vector aun está expresado en el sistema de referencia “1”. Para pasar al “2” debemos relacionar las bases respectivas. Las relaciones son

Podemos obtener el vector de expresión en la base “2” simplemente observando que

donde podemos reconocer los vectores de la base, por lo que

La obtención de la velocidad inversa es entonces trivial

y la velocidad que pide el enunciado es

CIR en el sistema “1”
Para hallar la posición del centro instantáneo de rotación disponemos de la fórmula analítica

siendo ya conocidas cada una de las cantidades. Sustituyendo

A la vista de este resultado tenemos que
- La posición del CIR no depende de la rapidez con la que varía el ángulo,
 .
.
- En este caso concreto, a medida que va variando
 , la posición de los sucesivos CCIIR se encuentra sobre una circunferencia de radio
, la posición de los sucesivos CCIIR se encuentra sobre una circunferencia de radio  en torno a
en torno a  .
.
CIR en el sistema “2”
De la misma manera puede calcularse la posición en el sistema “2”. Para expresar este resultado, debemos hallar el vector de posición relativo a  y expresarla en el sistema de ejes ligado al sólido “2”.
y expresarla en el sistema de ejes ligado al sólido “2”.
Esto lo podemos conseguir de varias formas:
- A partir de la velocidad de

- Puesto que hemos calculado previamente la velocidad de
 podemos volver a aplicar la fórmula analítica para la posición del CIR
podemos volver a aplicar la fórmula analítica para la posición del CIR

- donde ahora

- Sustituyendo

- A partir de la posición relativa a

- Puesto que ya hemos determinado la posición del CIR relativa a
 , para hallar la posición relativo a
, para hallar la posición relativo a  nos basta con sumar vectores
nos basta con sumar vectores

- donde, como hemos visto

- y

- Sumando estas dos expresiones

Vemos que este CIR se mueve a lo largo de la recta correspondiente al eje 
Interpretación de los resultados
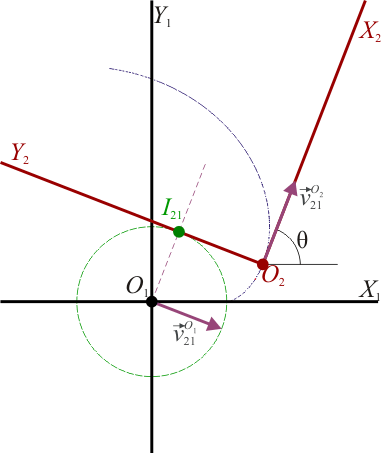
De acuerdo con los resultados anteriores, hemos obtenido que, a medida que aumenta el valor del ángulo  , la posición del CIR
, la posición del CIR  va desplazándose a lo largo de una circunferencia, según el sistema del sólido “1” y a lo largo de una recta, según el sólido “2”. Este resultado posee una interpretación geométrica sencilla.
va desplazándose a lo largo de una circunferencia, según el sistema del sólido “1” y a lo largo de una recta, según el sólido “2”. Este resultado posee una interpretación geométrica sencilla.
Cuando varía  el punto
el punto  va describiendo la evolvente de una circunferencia. Este curva puede describirse como la posición que ocupa el extremo de un hilo tenso, pero también es la que curva que corresponde al extremo de una barra recta que rueda sin deslizar sobre un disco circular.
va describiendo la evolvente de una circunferencia. Este curva puede describirse como la posición que ocupa el extremo de un hilo tenso, pero también es la que curva que corresponde al extremo de una barra recta que rueda sin deslizar sobre un disco circular.
Empleando esta interpretación vemos que es natural que las sucesivas posiciones del CIR se encuentren sobre una circunferencia, en el sistema ligado a ésta, y sobre una recta, en el sistema ligado a la barra.

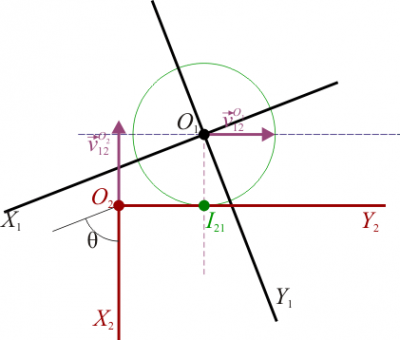
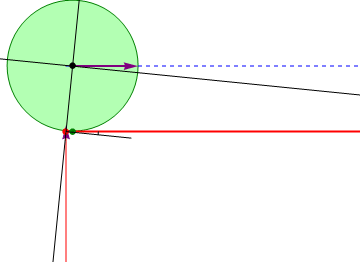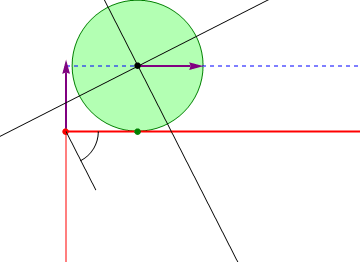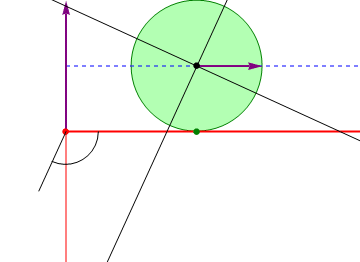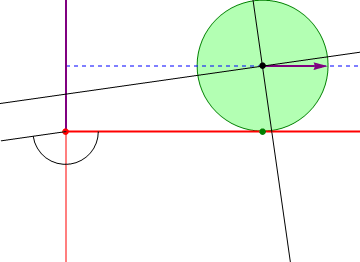
Este movimiento puede también verse de manera inversa. Considerando como sistema fijo el “2” y como móvil el “1”, el sistema equivalente pasa a ser el de un disco que rueda sobre una superficie horizontal. Con esta reinterpretación, es inmediato que el vector de posición relativa  en el sistema “2” se exprese como un vector constante,
en el sistema “2” se exprese como un vector constante,  , ya que se trata del vector que une el centro del disco con el punto de apoyo, y esta posición relativa es constante.
, ya que se trata del vector que une el centro del disco con el punto de apoyo, y esta posición relativa es constante.








































