Ejemplo de movimiento helicoidal

Enunciado

Una partícula se mueve a lo largo de la hélice descrita por la ecuación paramétrica

${\vec {r}}(\theta )=A\cos(\theta ){\vec {\imath }}+A\,\mathrm {sen} (\theta ){\vec {\jmath }}+{\frac {b\theta }{2\pi }}{\vec {k}}$

donde $A$ y $b$ son constantes conocidas. El movimiento de la partícula sigue la ley horaria

$\theta (t)=\Omega _{0}t+\beta t^{2}\,$

donde $\Omega _{0}$ y $\beta$ son constantes conocidas.

1. Determine el parámetro arco de la hélice descrita, como función del parámetro $\theta$ y como función del tiempo.
2. Halle la rapidez del movimiento.
3. Calcule la componente tangencial de la aceleración de la partícula en todo instante.
4. Para el instante $t=0$ calcule la velocidad y la aceleración de la partícula.
5. Para el mismo instante, halle los vectores del triedro de Frenet, así como el radio de curvatura de la partícula y su aceleración normal.

Parámetro arco

Podemos determinar el parámetro arco empleando la variable $\theta$ según la relación

${\frac {\mathrm {d} s}{\mathrm {d} \theta }}=\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} \theta }}\right|$

Derivando y calculando el módulo

${\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} \theta }}=-A\,\mathrm {sen} (\theta ){\vec {\imath }}+A\cos(\theta ){\vec {\jmath }}+{\frac {b}{2\pi }}{\vec {k}}$

El módulo de este vector vale

$\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} \theta }}\right|={\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$

Puesto que el módulo es independiente de $\theta$, su integración es inmediata

${\frac {\mathrm {d} s}{\mathrm {d} \theta }}={\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$ ⇒  $s=\theta {\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$

Y para obtener el parámetro arco en función del tiempo, basta sustituir en $s(\theta )$ la ley horaria $\theta (t)$ del enunciado

$s=(\Omega _{0}t+\beta t^{2}){\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$

Celeridad

El cálculo de la rapidez es inmediato por derivación respecto al tiempo del parámetro arco

$v={\dot {s}}=\left(\Omega _{0}+2\beta t\right){\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$

Aceleración tangencial

Obtenemos la componente tangencial de la aceleración derivando la celeridad respecto al tiempo

$a_{t}={\dot {v}}={\ddot {s}}=2\beta {\sqrt {A^{2}+{\frac {b^{2}}{4\pi ^{2}}}}}$

Puesto que esta aceleración tangencial es constante, el movimiento a lo largo de la hélice es uniformemente acelerado.

Velocidad y aceleración iniciales

Hallamos la ecuación horaria sustituyendo la ley horaria en la ecuación de la trayectoria

${\vec {r}}(t)=A\cos(\Omega _{0}t+\beta t^{2}){\vec {\imath }}+A\,\mathrm {sen} (\Omega _{0}t+\beta t^{2}){\vec {\jmath }}+{\frac {b(\Omega _{0}t+\beta t^{2})}{2\pi }}{\vec {k}}$

Derivando en esta expresión respecto al tiempo

${\vec {v}}(t)={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}=\left(\Omega _{0}+2\beta t\right)\left(-A\,\mathrm {sen} (\Omega _{0}t+\beta t^{2}){\vec {\imath }}+A\cos(\Omega _{0}t+\beta t^{2}){\vec {\jmath }}+{\frac {b}{2\pi }}{\vec {k}}\right)$

Haciendo $t=0$

${\vec {v}}(0)=\Omega _{0}\left(A{\vec {\jmath }}+{\frac {b}{2\pi }}{\vec {k}}\right)$

Obtenemos la aceleración derivando la velocidad respecto al tiempo

${\vec {a}}(t)={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}=2\beta \left(-A\,\mathrm {sen} (\Omega _{0}t+\beta t^{2}){\vec {\imath }}+A\cos(\Omega _{0}t+\beta t^{2}){\vec {\jmath }}+{\frac {b}{2\pi }}{\vec {k}}\right)$ $+\left(\Omega _{0}+2\beta t\right)^{2}\left(-A\cos(\Omega _{0}t+\beta t^{2}){\vec {\imath }}-A\,\mathrm {sen} (\Omega _{0}t+\beta t^{2}){\vec {\jmath }}\right)$

Haciendo aquí $t=0$

${\vec {a}}(0)=-\Omega _{0}^{2}A{\vec {\imath }}+2\beta A{\vec {\jmath }}+{\frac {b\beta }{\pi }}{\vec {k}}$

Triedro de Frenet

Para el instante inicial hallamos el vector tangente a la circunferencia normalizando la velocidad

${\vec {T}}(0)={\frac {{\vec {v}}(0)}{v(0)}}={\frac {1}{\sqrt {A^{2}+{b^{2}}/{4\pi ^{2}}}}}\left(A{\vec {\jmath }}+{\frac {b}{2\pi }}{\vec {k}}\right)$

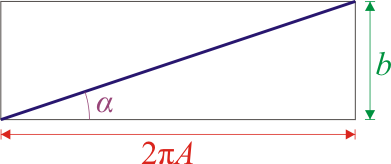
Si lo escribimos en función de la inclinación de la hélice, $\alpha$, definida en la teoría, queda:

${\vec {T}}(0)=\cos(\alpha ){\vec {\jmath }}+\mathrm {sen} (\alpha ){\vec {k}}$

siendo evidente a partir de la figura que:

$\cos(\alpha )={\frac {A}{\sqrt {A^{2}+{b^{2}}/{4\pi ^{2}}}}}$   ;     $\mathrm {sen} (\alpha )={\frac {b/2\pi }{\sqrt {A^{2}+{b^{2}}/{4\pi ^{2}}}}}$

El vector binormal lo hallamos normalizando el producto vectorial de la velocidad y la aceleración:

${\vec {v}}(0)\times {\vec {a}}(0)=\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&\Omega _{0}A&\Omega _{0}b/2\pi \\-\Omega _{0}^{2}A&2\beta A&b\beta /\pi \end{matrix}}\right|=A\Omega _{0}^{3}\left(-{\frac {b}{2\pi }}{\vec {\jmath }}+A{\vec {k}}\right)$

Resulta el vector

${\vec {B}}(0)={\frac {1}{\sqrt {A^{2}+{b^{2}}/{4\pi ^{2}}}}}\left(-{\frac {b}{2\pi }}{\vec {\jmath }}+A{\vec {k}}\right)$

que es claramente ortogonal al vector tangente.

Escrito en función de $\alpha$:

${\vec {B}}(0)=-\mathrm {sen} (\alpha ){\vec {\jmath }}+\cos(\alpha ){\vec {k}}$

Multiplicando estos dos hallamos el vector normal

${\vec {N}}(0)={\vec {B}}(0)\times {\vec {T}}(0)={\frac {1}{A^{2}+b^{2}/4\pi ^{2}}}\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&-b\beta /\pi &A\\0&A&b/2\pi \end{matrix}}\right|=-{\vec {\imath }}$

que es ortogonal a los dos anteriores.

De aquí tenemos que la aceleración normal en el instante inicial es igual a

$a_{n}(0)={\vec {a}}(0)\cdot (-{\vec {\imath }})=A\Omega _{0}^{2}$

y el radio de curvatura inicial vale

$R(0)={\frac {v^{2}(0)}{a_{n}(0)}}={\frac {\Omega _{0}^{2}\left(A^{2}+b^{2}/4\pi ^{2}\right)}{A\Omega _{0}^{2}}}=A+{\frac {b^{2}}{4\pi ^{2}A}}$

Puede demostrarse que este radio de curvatura es constante a lo largo de todo el movimiento.

Método alternativo: Tras calcular ${\vec {T}}(0)$, podríamos haber calculado el vector aceleración normal como:

${\vec {a}}_{n}(0)={\vec {a}}(0)-a_{t}{\vec {T}}(0)=-A\Omega _{0}^{2}{\vec {\imath }}$

Tomando módulo y normalizando, obtendríamos la aceleración normal y el vector normal principal, respectivamente:

$a_{n}(0)=|{\vec {a}}_{n}(0)|=A\Omega _{0}^{2}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,{\vec {N}}(0)={\frac {{\vec {a}}_{n}(0)}{a_{n}(0)}}=-{\vec {\imath }}$

Y el vector binormal se obtendría entonces como ${\vec {B}}(0)={\vec {T}}(0)\times {\vec {N}}(0)$