Diferencia entre las páginas «Tres barras con simetría, Noviembre 2015 (MR G.I.C.)» y «Momento de inercia de un sólido compuesto de cuatro barras y un aro»
(Página creada con «== Enunciado == right El sistema de la figura es un modelo muy simplificado de hélice de un aerogenerador. Consta de tres barras iguales, de masas <math>M</math> y longitud <math>L</math>, soldadas en el punto <math>O</math>, de modo que forman un sólo sólido rígido. El ángulo entre las tres barras es el mismo. # Calcula el momento de inercia respecto al eje <math>OZ_1</math> en <math>O</math>. # Calcula el tensor de in…») |
(Página creada con «= Enunciado = right El sólido de la figura está compuesto de un aro delgado de masa <math>m</math> y radio <math>R</math>, así como de cuatro barras delgadas, cada una de masa <math>m</math> y longitud <math>R</math>, dispuestas como se indica en la figura. Todos los cuerpos son homogéneos. #Calcula el momento de inercia <math>I_{zz}</math>. #Calcula el tensor de inercia en <math>O</math> expresado en los ejes cartesianos de la figura…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Imagen: | [[Imagen:MR_Aro_barras.png|right]] | ||
El | El sólido de la figura está compuesto de un aro delgado de masa <math>m</math> y radio <math>R</math>, así como de | ||
cuatro barras delgadas, cada una de masa <math>m</math> y longitud <math>R</math>, dispuestas como se indica en la | |||
# Calcula el | figura. Todos los cuerpos son homogéneos. | ||
# | #Calcula el momento de inercia <math>I_{zz}</math>. | ||
#Calcula el tensor de inercia en <math>O</math> expresado en los ejes cartesianos de la figura. | |||
#Calcula el momento de inercia respecto al eje <math>\Delta</math> de la figura. | |||
= Solución = | |||
== Momento de inercia <math>I_{zz}</math> == | |||
El momento de inercia | |||
El momento de inercia pedido es | |||
<center> | <center> | ||
<math> | <math> | ||
I_{zz} = \int\limits_V \mathrm{d}m\,a^2 | |||
</math> | </math> | ||
</center> | </center> | ||
donde <math>a </math> es la distancia de cada punto del sólido al eje. | donde la integral se extiende a todo el sólido y <math>a</math> es la distancia de cada punto | ||
del sólido al eje <math>OZ</math>. Aplicamos la propiedad distributiva de la suma y separamos | |||
la integral en cuatro partes, una por cada barra de longitud <math>R</math> y otra por el aro. Las integrales para las barras son iguales, por simetría. | |||
<center> | <center> | ||
<math> | <math> | ||
I_{zz} = 4\int\limits_{barra} \mathrm{d}m\,a^2 + \int\limits_{aro} \mathrm{d}m\,a^2 | |||
</math> | </math> | ||
</center> | </center> | ||
Para las barras tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\int\limits_{\mathrm{ | I^{barra}_{zz} = \int\limits_{barra} \mathrm{d}m\,a^2 = | ||
\int\limits_{0}^R \dfrac{M}{R}\mathrm{d}y\,y^2 | |||
= | = | ||
\dfrac{1}{3} | \dfrac{1}{3}mR^3. | ||
</math> | </math> | ||
</center> | </center> | ||
Para el aro | |||
<center> | <center> | ||
<math> | <math> | ||
I = | I^{aro}_{zz} = \int\limits_{aro} \mathrm{d}m\,R^2 = R^2\,\int\limits_{aro} \mathrm{d}m = mR^2 | ||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
Entonces | |||
<center> | <center> | ||
<math> | <math> | ||
I_{ | I_{zz} = 4\,\dfrac{mR^2}{3} + mR^2 = \dfrac{7}{3}mR^2. | ||
</math> | </math> | ||
</center> | </center> | ||
< | == Tensor de inercia en <math>O</math> == | ||
<math> | Por simetría, los ejes <math>X</math> e <math>Y</math> son direcciones principales de | ||
inercia. El eje <math>Z</math> lo es por ser un sólido plano. Entonces el tensor es | |||
</math> | diagonal en los ejes de la figura. Aplicando el teorema de los ejes perpendiculares | ||
</ | |||
<center> | <center> | ||
<math> | <math> | ||
I_{zz} = I_{xx} + I_{yy} | |||
= | |||
</math> | </math> | ||
</center> | </center> | ||
y por simetría | |||
<center> | <center> | ||
<math> | <math> | ||
I_{xx} = I_{yy}. | |||
</math> | </math> | ||
</center> | </center> | ||
Por tanto | |||
<center> | <center> | ||
<math> | <math> | ||
I_{xx} = I_{yy} = \dfrac{1}{2}I_{zz} = \dfrac{7}{6}mR^2. | |||
</math> | </math> | ||
</center> | </center> | ||
El | El tensor de inercia es | ||
<center> | <center> | ||
<math> | <math> | ||
\overleftrightarrow{I}_O | |||
= | = | ||
\dfrac{ | \dfrac{7mR^2}{6} | ||
\left[ | \left[ | ||
\begin{array}{ccc} | \begin{array}{ccc} | ||
| Línea 98: | Línea 82: | ||
\end{array} | \end{array} | ||
\right] | \right] | ||
</math> | </math> | ||
</center> | </center> | ||
== | == Momento de inercia respecto a <math>\Delta</math> == | ||
Hemos visto que | |||
= | |||
= | |||
<center> | <center> | ||
<math> | <math> | ||
I_{xx} = \dfrac{7}{6}mR^2 | |||
= | |||
\dfrac{ | |||
</math> | </math> | ||
</center> | </center> | ||
Aplicando el Teorema de los ejes paralelos tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
I_{\Delta} = I_{xx} + 5mR^2 = \dfrac{37}{6}mR^2. | |||
\ | |||
= | |||
\dfrac{ | |||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría:Problemas de cinética del sólido rígido]] | [[Categoría:Problemas de cinética del sólido rígido]] | ||
[[Categoría:Problemas de examen de Mecánica Racional]] | [[Categoría:Problemas de examen de Mecánica Racional]] | ||
Revisión actual - 16:51 17 oct 2023
Enunciado
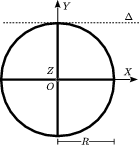
El sólido de la figura está compuesto de un aro delgado de masa y radio , así como de cuatro barras delgadas, cada una de masa y longitud , dispuestas como se indica en la figura. Todos los cuerpos son homogéneos.
- Calcula el momento de inercia .
- Calcula el tensor de inercia en expresado en los ejes cartesianos de la figura.
- Calcula el momento de inercia respecto al eje de la figura.
Solución
Momento de inercia
El momento de inercia pedido es
donde la integral se extiende a todo el sólido y es la distancia de cada punto del sólido al eje . Aplicamos la propiedad distributiva de la suma y separamos la integral en cuatro partes, una por cada barra de longitud y otra por el aro. Las integrales para las barras son iguales, por simetría.
Para las barras tenemos
Para el aro
Entonces
Tensor de inercia en
Por simetría, los ejes e son direcciones principales de inercia. El eje lo es por ser un sólido plano. Entonces el tensor es diagonal en los ejes de la figura. Aplicando el teorema de los ejes perpendiculares
y por simetría
Por tanto
El tensor de inercia es
Momento de inercia respecto a
Hemos visto que
Aplicando el Teorema de los ejes paralelos tenemos


















![{\displaystyle {\overleftrightarrow {I}}_{O}={\dfrac {7mR^{2}}{6}}\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/169149642efdac119c8d4ebcc9cff1e7eb015c09)

