Diferencia entre las páginas «Archivo:MR Aro barras.png» y «Tres barras con simetría, Noviembre 2015 (MR G.I.C.)»
Sin resumen de edición |
(Página creada con «== Enunciado == right El sistema de la figura es un modelo muy simplificado de hélice de un aerogenerador. Consta de tres barras iguales, de masas <math>M</math> y longitud <math>L</math>, soldadas en el punto <math>O</math>, de modo que forman un sólo sólido rígido. El ángulo entre las tres barras es el mismo. # Calcula el momento de inercia respecto al eje <math>OZ_1</math> en <math>O</math>. # Calcula el tensor de in…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | |||
[[Imagen:Tres_barras_enunciado_PPC_MR.png|right]] | |||
El sistema de la figura es un modelo muy simplificado de hélice de un aerogenerador. Consta de tres barras iguales, de masas <math>M</math> y longitud <math>L</math>, soldadas en el punto <math>O</math>, de modo que forman un sólo sólido rígido. El ángulo entre las tres barras es el mismo. | |||
# Calcula el momento de inercia respecto al eje <math>OZ_1</math> en <math>O</math>. | |||
# Calcula el tensor de inercia en <math>O</math>. | |||
# El sólido rota alrededor de un eje que pasa por <math>O</math>, está contenido en el plano <math>OX_1Z_1</math> y forma un ángulo <math>\pi/4</math> con el eje <math>OX_1</math>. Calcula el momento de inercia del sólido alrededor de ese eje. | |||
#Si el vector de rotación tiene módulo <math>\omega_0</math> y apunta hacia los sentidos positivos de los ejes <math>OX_1</math> y <math>OZ_1</math>, calcula el coseno del ángulo que forman el momento cinético y el vector rotación. | |||
#En este último caso, calcula la energía cinética. | |||
== Solución == | |||
=== Momento de inercia === | |||
El momento de inercia de un sólido respecto a un eje es | |||
<center> | |||
<math> | |||
I = \int\,\mathrm{d}m\,a^2 | |||
</math> | |||
</center> | |||
donde <math>a </math> es la distancia de cada punto del sólido al eje. En este caso, la integral se compone de tres integrales, una para cada barra: | |||
<center> | |||
<math> | |||
I = 3\int\limits_{\mathrm{barra}}\,\mathrm{d}m\,a^2 | |||
</math> | |||
</center> | |||
Pero para cada barra la integral es el momento de inercia respecto de un eje perpendicular a ella que pasa por su extremo: | |||
<center> | |||
<math> | |||
\int\limits_{\mathrm{barra}}\,\mathrm{d}m\,a^2 | |||
= | |||
\dfrac{1}{3}ML^2 | |||
</math> | |||
</center> | |||
Por tanto el momento de inercia pedido es | |||
<center> | |||
<math> | |||
I = 3 | |||
\dfrac{1}{3}ML^2 = ML^2 | |||
</math> | |||
</center> | |||
=== Tensor de inercia en O === | |||
El sistema es plano, por lo que el eje <math>OZ_1 </math> es eje principal de inercia. Además tiene simetría respecto al eje <math>OZ_1 </math>, pues en ángulo entre las barras es el mismo. Por tanto, todas las direcciones en el plano <math>O_1X_1Y_1 </math> son direcciones principales de inercia, y el tensor de inercia en <math>O </math> es diagonal cuando se expresa en los ejes de la figura. | |||
Por ser el sistema plano | |||
<center> | |||
<math> | |||
I_{33} = I_{11} + I_{22} | |||
</math> | |||
</center> | |||
A causa de la simetría <math>I_{11} = I_{22} </math>, por lo que | |||
<center> | |||
<math> | |||
I_{11} = I_{22} = \dfrac{1}{2}I_{33} = \dfrac{1}{2}I = \dfrac{1}{2}ML^2 | |||
</math> | |||
</center> | |||
El tensor de inercia pedido es | |||
<center> | |||
<math> | |||
\overleftrightarrow{I}_O | |||
= | |||
\dfrac{ML^2}{2} | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 2 | |||
\end{array} | |||
\right] | |||
</math> | |||
</center> | |||
=== Momento de inercia respecto a un eje de rotación === | |||
Por lo que dice el enunciado el vector rotación es | |||
<center> | |||
<math> | |||
\vec{\omega} = \omega_0\,\left[\dfrac{1}{\sqrt{2}}, 0, \dfrac{1}{\sqrt{2}}\right] | |||
</math> | |||
</center> | |||
Un vector unitario en esa dirección es | |||
<center> | |||
<math> | |||
\vec{n} = \left[\dfrac{1}{\sqrt{2}}, 0, \dfrac{1}{\sqrt{2}}\right] | |||
</math> | |||
</center> | |||
El momento de inercia respecto del eje es | |||
<center> | |||
<math> | |||
I_{\Delta} = | |||
\vec{n}\cdot\overleftrightarrow{I}_O\cdot\vec{n} | |||
= | |||
\dfrac{ML^2}{2} | |||
\left[\dfrac{1}{\sqrt{2}}, 0, \dfrac{1}{\sqrt{2}}\right] | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 2 | |||
\end{array} | |||
\right] | |||
\left[ | |||
\begin{array}{c} | |||
\dfrac{1}{\sqrt{2}} \\ 0 \\ \dfrac{1}{\sqrt{2}} | |||
\end{array} | |||
\right] | |||
= | |||
\dfrac{3}{4}ML^2 | |||
</math> | |||
</center> | |||
=== Ángulo entre los vectores rotación y momento cinético === | |||
Como <math>O </math> es un punto fijo, el momento cinético del sólido es | |||
<center> | |||
<math> | |||
\vec{L}_O | |||
= | |||
\overleftrightarrow{I}_O\cdot\vec{\omega} | |||
= | |||
\dfrac{ML^2}{2} | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 2 | |||
\end{array} | |||
\right] | |||
\left[ | |||
\begin{array}{c} | |||
\dfrac{1}{\sqrt{2}} \\ 0 \\ \dfrac{1}{\sqrt{2}} | |||
\end{array} | |||
\right] | |||
= | |||
\dfrac{ML^2}{2} | |||
\left[ | |||
\begin{array}{c} | |||
\dfrac{1}{\sqrt{2}} \\ 0 \\ \sqrt{2} | |||
\end{array} | |||
\right] | |||
</math> | |||
</center> | |||
El coseno del ángulo entre los vectores rotación y momento cinético es | |||
<center> | |||
<math> | |||
\cos\alpha = \dfrac{\vec{L}_O\cdot\vec{\omega}}{|\vec{L}_O||\vec{\omega}|} | |||
= | |||
\dfrac{3}{\sqrt{10}} | |||
</math> | |||
</center> | |||
=== Energía cinética === | |||
Al ser un punto fijo, la energía cinética del sólido es | |||
<center> | |||
<math> | |||
T = | |||
\dfrac{1}{2} | |||
\vec{\omega}\cdot\overleftrightarrow{I}_O\cdot\vec{\omega} | |||
= | |||
\dfrac{ML^2\omega_0^2}{2} | |||
\left[\dfrac{1}{\sqrt{2}}, 0, \dfrac{1}{\sqrt{2}}\right] | |||
\left[ | |||
\begin{array}{ccc} | |||
1 & 0 & 0\\ | |||
0 & 1 & 0\\ | |||
0 & 0 & 2 | |||
\end{array} | |||
\right] | |||
\left[ | |||
\begin{array}{c} | |||
\dfrac{1}{\sqrt{2}} \\ 0 \\ \dfrac{1}{\sqrt{2}} | |||
\end{array} | |||
\right] | |||
= | |||
\dfrac{3}{8}ML^2\omega_0^2 | |||
</math> | |||
</center> | |||
[[Categoría:Problemas de cinética del sólido rígido]] | |||
[[Categoría:Problemas de dinámica del sólido rígido (MR)]] | |||
[[Categoría:Problemas de dinámica del sólido rígido]] | |||
[[Categoría:Problemas de dinámica del sólido rígido (MR)]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión actual - 16:50 17 oct 2023
Enunciado
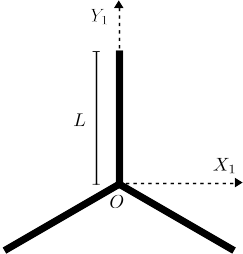
El sistema de la figura es un modelo muy simplificado de hélice de un aerogenerador. Consta de tres barras iguales, de masas y longitud , soldadas en el punto , de modo que forman un sólo sólido rígido. El ángulo entre las tres barras es el mismo.
- Calcula el momento de inercia respecto al eje en .
- Calcula el tensor de inercia en .
- El sólido rota alrededor de un eje que pasa por , está contenido en el plano y forma un ángulo con el eje . Calcula el momento de inercia del sólido alrededor de ese eje.
- Si el vector de rotación tiene módulo y apunta hacia los sentidos positivos de los ejes y , calcula el coseno del ángulo que forman el momento cinético y el vector rotación.
- En este último caso, calcula la energía cinética.
Solución
Momento de inercia
El momento de inercia de un sólido respecto a un eje es
donde es la distancia de cada punto del sólido al eje. En este caso, la integral se compone de tres integrales, una para cada barra:
Pero para cada barra la integral es el momento de inercia respecto de un eje perpendicular a ella que pasa por su extremo:
Por tanto el momento de inercia pedido es
Tensor de inercia en O
El sistema es plano, por lo que el eje es eje principal de inercia. Además tiene simetría respecto al eje , pues en ángulo entre las barras es el mismo. Por tanto, todas las direcciones en el plano son direcciones principales de inercia, y el tensor de inercia en es diagonal cuando se expresa en los ejes de la figura.
Por ser el sistema plano
A causa de la simetría , por lo que
El tensor de inercia pedido es
Momento de inercia respecto a un eje de rotación
Por lo que dice el enunciado el vector rotación es
Un vector unitario en esa dirección es
El momento de inercia respecto del eje es
Ángulo entre los vectores rotación y momento cinético
Como es un punto fijo, el momento cinético del sólido es
El coseno del ángulo entre los vectores rotación y momento cinético es
Energía cinética
Al ser un punto fijo, la energía cinética del sólido es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 16:49 17 oct 2023 |  | 140 × 145 (5 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:

















![{\displaystyle {\overleftrightarrow {I}}_{O}={\dfrac {ML^{2}}{2}}\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e91ac32d15a591aa8eb8b22b114a474e02a88aa)
![{\displaystyle {\vec {\omega }}=\omega _{0}\,\left[{\dfrac {1}{\sqrt {2}}},0,{\dfrac {1}{\sqrt {2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c611499d226d098477b3bf9b9a44dcbd0195257)
![{\displaystyle {\vec {n}}=\left[{\dfrac {1}{\sqrt {2}}},0,{\dfrac {1}{\sqrt {2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0c330a6e563cb4aaca2b7892f846f1804ff9399)
![{\displaystyle I_{\Delta }={\vec {n}}\cdot {\overleftrightarrow {I}}_{O}\cdot {\vec {n}}={\dfrac {ML^{2}}{2}}\left[{\dfrac {1}{\sqrt {2}}},0,{\dfrac {1}{\sqrt {2}}}\right]\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]\left[{\begin{array}{c}{\dfrac {1}{\sqrt {2}}}\\0\\{\dfrac {1}{\sqrt {2}}}\end{array}}\right]={\dfrac {3}{4}}ML^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7be0fbca06fb3ec83f1fa8edf5c1467a0b0fc99)
![{\displaystyle {\vec {L}}_{O}={\overleftrightarrow {I}}_{O}\cdot {\vec {\omega }}={\dfrac {ML^{2}}{2}}\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]\left[{\begin{array}{c}{\dfrac {1}{\sqrt {2}}}\\0\\{\dfrac {1}{\sqrt {2}}}\end{array}}\right]={\dfrac {ML^{2}}{2}}\left[{\begin{array}{c}{\dfrac {1}{\sqrt {2}}}\\0\\{\sqrt {2}}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e429da690708ea314052bce9ba37e764adf96dad)

![{\displaystyle T={\dfrac {1}{2}}{\vec {\omega }}\cdot {\overleftrightarrow {I}}_{O}\cdot {\vec {\omega }}={\dfrac {ML^{2}\omega _{0}^{2}}{2}}\left[{\dfrac {1}{\sqrt {2}}},0,{\dfrac {1}{\sqrt {2}}}\right]\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]\left[{\begin{array}{c}{\dfrac {1}{\sqrt {2}}}\\0\\{\dfrac {1}{\sqrt {2}}}\end{array}}\right]={\dfrac {3}{8}}ML^{2}\omega _{0}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecdb894199461292d292dc5b8dfe7c17c21fa9a5)