Diferencia entre las páginas «No Boletín - Ecuaciones horarias en coordenadas polares (Ex.Feb/14)» y «No Boletín - Equilibrio de partícula en parábola»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
Una partícula de masa <math>m</math> se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte de constante <math>k</math> y longitud natural nula anclado en el punto <math>\vec{r}_0=\vec{0}</math>. La partícula está ensartada en la parábola <math>z = -x^2/(2b)</math>. | |||
# Determine la(s) posición(es) de equilibrio de la masa sobre la parábola. | |||
<center><math> | # Calcule la fuerza de reacción vincular de la parábola sobre la partícula en la(s) posición(es) de equilibrio. | ||
\ | # Trace la curva de la energía potencial como función de la coordenada <math>x</math> y discuta la estabilidad de las posibles posiciones de equilibrio. | ||
==Equilibrio== | |||
La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle | |||
y la fuerza de reacción vincular. En el equilibrio, la resultante debe ser nula | |||
<center><math>m\vec{g}-k\vec{r}+\vec{\Phi}=\vec{0}</math></center> | |||
Junto a esta ecuación tenemos la del vínculo | |||
<center><math>z = -\frac{x^2}{2b}</math></center> | |||
Separando en las componentes cartesianas tenemos, para el peso | |||
<center><math>m\vec{g}=-mg\vec{k}</math></center> | |||
y para la fuerza elástica | |||
<center><math>-k\vec{r}=-kx\vec{\imath}-kz\vec{k}=-kx\vec{\imath}+\frac{kx^2}{2b}\vec{k} | |||
</math></center> | </math></center> | ||
La fuerza de reacción vincular va en la dirección normal a la parábola y contenida en el | |||
plano OXZ (pues no hay fuerzas activas en la dirección de OY). El vector tangente a la | |||
parábola | |||
<center><math>\vec{r}=x\vec{\imath}-\frac{x^2}{2b}\vec{k}</math></center> | |||
es | |||
<center><math>\vec{T}=\frac{\mathrm{d}\vec{r}/\mathrm{d}x}{|\mathrm{d}\vec{r}/\mathrm{d}x|}= | |||
\frac{\vec{\imath}-(x/b)\vec{k}}{\sqrt{1+(x/b)^2}}</math></center> | |||
El vector normal es el perpendicular a este | |||
<center><math>\vec{N}=\frac{(x/b)\vec{\imath}+\vec{k}}{\sqrt{1+(x/b)^2}}</math></center> | |||
La fuerza de reacción vincular es paralela a este vector, por lo que puede escribirse | |||
como | |||
<center><math>\vec{\Phi}=\lambda\left((x/b)\vec{\imath}+\vec{k}\right) | |||
<center><math> | |||
\vec{ | |||
\vec | |||
</math></center> | </math></center> | ||
Sustituyendo y separando en las componentes tenemos las ecuaciones | |||
<center><math>-kx + \frac{\lambda x}{b} = 0 | |||
<center><math> | |||
</math></center> | </math></center> | ||
y | |||
<center><math> | <center><math>-mg+\frac{kx^2}{2b}+\lambda = 0</math></center> | ||
</math></center> | donde las incógnitas son x (posición de equilibrio) y <math>\lambda</math>, que da la intensidad de | ||
la fuerza de reacción vincular. | |||
<center><math> | |||
Este sistema admite, en cualquier caso, la solución | |||
</math></center> | |||
<center><math>x=0\qquad\qquad\lambda=mg\qquad\qquad\vec{\Phi}=mg\vec{k}</math></center> | |||
En esta posición, situada en el vértice de la parábola, el resorte no ejerce fuerza | |||
alguna y la reacción es igual y opuesta al peso. | |||
Si <math>x \neq 0</math> tenemos | |||
<center><math>\lambda = kb</math></center> | |||
y sustituyendo en la segunda | |||
<center><math>x =\pm \sqrt{\frac{2b}{k}(mg-kb)}</math></center> | |||
La existencia o no de nuevas posiciones de reposo depende de la relación entre las | |||
distintas constantes. Si la masa es lo suficientemente grande como para que | |||
<center><math>\frac{mg}{kb}>1</math></center> | |||
Existen tres puntos de equilibrio, el del vértice y dos situados simétricamente a sus | |||
lados. | |||
Si la masa es pequeña y esta combinación es menor que la unidad, el único punto de | |||
equilibrio es el del vértice. | |||
Físicamente podemos ver que si la masa es grande, el peso es dominante y tira de la masa | |||
hacia abajo por la parábola, hasta que la fuerza recuperadora del resorte es capaz de | |||
retenerla. Si la masa es pequeña, la fuerza recuperadora es la dominante y la gravedad no | |||
es capaz de sacarla del equilibrio de la posición central. | |||
==Fuerza de reacción== | |||
===Posición central=== | |||
Según indicamos, en la posición central, la fuerza de reacción vincular compensa al peso | |||
<center><math>\vec{\Phi}=mg\vec{k}</math></center> | |||
===Posiciones laterales=== | |||
Si se da el caso de que existen las dos posiciones de equilibrio adicionales, la fuerza | |||
de reacción vincular en ellas vale | |||
<center><math>\lambda = kb\qquad\qquad \vec{\Phi}=\lambda\frac{x}{b}\vec{\imath}+\lambda\vec{k}= | |||
\pm kb\sqrt{2\left(\frac{mg}{kb}-1\right)}\vec{\imath}+kb\vec{k}</math></center> | |||
==Energía potencial== | |||
[[Archivo:potencial-muelle-parabola.png|right]] | |||
Puesto que la fuerza de reacción es normal, la energía potencial es la asociada a la gravedad y a la fuerza elástica | |||
<center><math>U=mgz + \frac{k}{2}(x^2+z^2) = | |||
<center><math> | -\frac{mgx^2}{2b}+\frac{k}{2}\left(x^2+\frac{x^4}{4b^2}\right) = \frac{kb-mg}{2b}x^2 + | ||
\frac{kx^4}{8b^2}</math></center> | |||
</math></center> | |||
La gráfica de esta función se caracteriza por que el exponente de mayor grado es par y su coeficiente es positivo, con lo que la función es creciente para <math>x\to\pm\infty</math>. Tenemos lo que se llama un ''pozo de potencial''. | |||
</math> | |||
El comportamiento en las proximidades de <math>x=0</math> lo da el coeficiente del término cuadrático. | |||
</math> | |||
Si <math>mg/kb < 1</math> este coeficiente es positivo y la energía potencial tiene un mínimo en <math>x=0</math>. Tenemos entonces un solo punto de equilibrio que además es de equilibrio estable. | |||
</math> | |||
Si <math>mg/kb > 1</math> el coeficiente es negativo y la energía potencial tiene un máximo en <math>x=0</math>. El vértice de la parábola es ahora un punto de equilibrio inestable. Puesto que la energía crece para |x| grande, debe haber un mínimo a cada lado del vértice. Estos son los dos puntos de equilibrio estable situados simétricamente respecto al vértice. | |||
[[Categoría:Problemas de Dinámica del Punto (GITI)]] | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión del 19:00 10 ene 2024
Enunciado
Una partícula de masa se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte de constante y longitud natural nula anclado en el punto . La partícula está ensartada en la parábola .
- Determine la(s) posición(es) de equilibrio de la masa sobre la parábola.
- Calcule la fuerza de reacción vincular de la parábola sobre la partícula en la(s) posición(es) de equilibrio.
- Trace la curva de la energía potencial como función de la coordenada y discuta la estabilidad de las posibles posiciones de equilibrio.
Equilibrio
La partícula se encuentra sometida a tres fuerzas: el peso, la fuerza elástica del muelle y la fuerza de reacción vincular. En el equilibrio, la resultante debe ser nula
Junto a esta ecuación tenemos la del vínculo
Separando en las componentes cartesianas tenemos, para el peso
y para la fuerza elástica
La fuerza de reacción vincular va en la dirección normal a la parábola y contenida en el plano OXZ (pues no hay fuerzas activas en la dirección de OY). El vector tangente a la parábola
es
El vector normal es el perpendicular a este
La fuerza de reacción vincular es paralela a este vector, por lo que puede escribirse como
Sustituyendo y separando en las componentes tenemos las ecuaciones
y
donde las incógnitas son x (posición de equilibrio) y , que da la intensidad de la fuerza de reacción vincular.
Este sistema admite, en cualquier caso, la solución
En esta posición, situada en el vértice de la parábola, el resorte no ejerce fuerza alguna y la reacción es igual y opuesta al peso.
Si tenemos
y sustituyendo en la segunda
La existencia o no de nuevas posiciones de reposo depende de la relación entre las distintas constantes. Si la masa es lo suficientemente grande como para que
Existen tres puntos de equilibrio, el del vértice y dos situados simétricamente a sus lados.
Si la masa es pequeña y esta combinación es menor que la unidad, el único punto de equilibrio es el del vértice.
Físicamente podemos ver que si la masa es grande, el peso es dominante y tira de la masa hacia abajo por la parábola, hasta que la fuerza recuperadora del resorte es capaz de retenerla. Si la masa es pequeña, la fuerza recuperadora es la dominante y la gravedad no es capaz de sacarla del equilibrio de la posición central.
Fuerza de reacción
Posición central
Según indicamos, en la posición central, la fuerza de reacción vincular compensa al peso
Posiciones laterales
Si se da el caso de que existen las dos posiciones de equilibrio adicionales, la fuerza de reacción vincular en ellas vale
Energía potencial
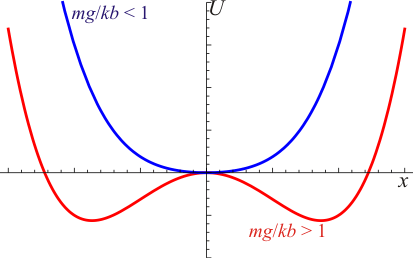
Puesto que la fuerza de reacción es normal, la energía potencial es la asociada a la gravedad y a la fuerza elástica
La gráfica de esta función se caracteriza por que el exponente de mayor grado es par y su coeficiente es positivo, con lo que la función es creciente para . Tenemos lo que se llama un pozo de potencial.
El comportamiento en las proximidades de lo da el coeficiente del término cuadrático.
Si este coeficiente es positivo y la energía potencial tiene un mínimo en . Tenemos entonces un solo punto de equilibrio que además es de equilibrio estable.
Si el coeficiente es negativo y la energía potencial tiene un máximo en . El vértice de la parábola es ahora un punto de equilibrio inestable. Puesto que la energía crece para |x| grande, debe haber un mínimo a cada lado del vértice. Estos son los dos puntos de equilibrio estable situados simétricamente respecto al vértice.



























