Diferencia entre las páginas «No Boletín - Ecuaciones horarias en coordenadas polares (Ex.Feb/14)» y «No Boletín - Ecuaciones horarias en coordenadas polares II (Ex.Ene/16)»
Secciones
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo:polares.png|right]] | [[Archivo:polares-con-base.png|right]] | ||
El movimiento de una partícula <math>\,P\,</math>, de masa <math>\,m\,</math>, en el plano <math>\,OXY\,</math> queda descrito en coordenadas polares mediante las ecuaciones horarias: | |||
El movimiento de una partícula <math>P\,</math>, de masa <math>m\,</math>, en el plano <math>OXY\,</math> queda descrito en coordenadas polares mediante las ecuaciones horarias: | |||
<center><math> | <center><math> | ||
\rho(t)= | \rho(t)=\rho_0\,(1+c\, t)\,\,\,;\,\,\,\,\,\,\,\,\theta(t)=\mathrm{ln}\,(1+c\, t) | ||
</math></center> | </math></center> | ||
siendo <math> | siendo <math>\,\rho_0\,</math> y <math>\,c\,</math> constantes positivas conocidas. | ||
# Determine la velocidad y la aceleración de la partícula en | # Determine la velocidad y la aceleración de la partícula (en la base polar <math>\,\{\vec{u}_{\rho},\vec{u}_{\theta}\}\!\,</math>). | ||
# Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria. | # Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria. | ||
# Calcule la energía cinética de la partícula, y la potencia | # Determine los vectores <math>\,\overrightarrow{T}\,</math> y <math>\,\overrightarrow{N}\,</math> del triedro intrínseco de la trayectoria de la partícula (en la base polar <math>\,\{\vec{u}_{\rho},\vec{u}_{\theta}\}\!\,</math>). | ||
# Calcule la energía cinética de la partícula, y la potencia desarrollada por la fuerza neta que actúa sobre ella. ¿Es la energía cinética una integral primera del movimiento? | |||
# Calcule el momento cinético de la partícula respecto al punto <math>\,O.\,</math> ¿Es el movimiento de la partícula un movimiento central con centro en <math>\,O\,</math>? Razone la respuesta. | |||
==Velocidad y aceleración== | ==Velocidad y aceleración== | ||
La velocidad y la aceleración en componentes polares vienen dadas por las expresiones: | La velocidad <math>\,\vec{v}\,</math> y la aceleración <math>\,\vec{a}\,</math> en componentes polares vienen dadas por las expresiones: | ||
<center><math> | <center><math> | ||
\vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta} | \vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta} | ||
\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{a}=\left(\ddot{\rho}-\rho\,\dot{\theta}^{2}\right) | \,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{a}=\left(\ddot{\rho}-\rho\,\dot{\theta}^{2}\right) | ||
\vec{u}_{\rho}+\left(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,\right) | \vec{u}_{\rho}+\left(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,\right)\vec{u}_{\theta} | ||
</math></center> | </math></center> | ||
Necesitamos, por tanto, calcular las derivadas de primer y segundo orden de <math>\rho\,</math> y <math>\theta\,</math> respecto al tiempo: | Necesitamos, por tanto, calcular las derivadas de primer y segundo orden de <math>\rho\,</math> y <math>\theta\,</math> respecto al tiempo: | ||
<center><math> | <center><math> | ||
\dot{\rho}= | \dot{\rho}=\rho_0\,c\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ddot{\rho}=0\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dot{\theta}=\frac{c}{1+c\,t}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ddot{\theta}=-\,\frac{c^{\, 2}}{(1+c\,t)^{\, 2}} | ||
</math></center> | </math></center> | ||
y sustituyendo en las expresiones de <math>\vec{v}\,</math> y <math>\vec{a}\,</math>, se obtiene: | y sustituyendo en las expresiones de <math>\,\vec{v}\,</math> y <math>\,\vec{a}\,</math>, se obtiene: | ||
<center><math> | <center><math> | ||
\vec{v}= | \vec{v}=\rho_0\,c\,(\vec{u}_{\rho}+\vec{u}_{\theta})\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, | ||
\vec{a}= | \vec{a}=\frac{\rho_0\,c^{\, 2}}{1+c\,t}\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta}) | ||
</math></center> | </math></center> | ||
==Componentes intrínsecas de la aceleración y radio de curvatura== | ==Componentes intrínsecas de la aceleración y radio de curvatura== | ||
Podemos calcular la | Podemos calcular la aceleración tangencial <math>\,a_t\,</math> como la derivada respecto al tiempo de la celeridad <math>\,v</math>: | ||
<center><math> | <center><math> | ||
v=|\vec{v}\,|= | v=|\vec{v}\,|=\sqrt{2}\,\rho_0\,c\,\,\,\,\,\longrightarrow\,\,\,\,\,a_t=\displaystyle\frac{\mathrm{d}v}{\mathrm{d}t}=0 | ||
</math></center> | </math></center> | ||
Otra posibilidad | Otra posibilidad es calcular <math>\,a_t\,</math> proyectando <math>\,\vec{a}\,</math> sobre la dirección de <math>\,\vec{v}</math> (que es tangente a la trayectoria): | ||
<center><math> | <center><math> | ||
a_t=\displaystyle\frac{\vec{v}\cdot\vec{a}}{v} | a_t=\displaystyle\frac{\vec{v}\cdot\vec{a}}{v}=0 | ||
</math></center> | </math></center> | ||
Al ser <math>\,a_t=0\,</math>, la aceleración normal <math>\,a_n\,</math> coincide con el módulo del vector aceleración (recuérdese que <math>\,a_n\geq 0</math> siempre): | |||
<center><math> | <center><math> | ||
a_n=\ | a_n=|\,\vec{a}\,|=\frac{\sqrt{2}\,\rho_0\,c^{\, 2}}{1+c\,t}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(\mathrm{en}\,\,\mathrm{general,}\,\,\,\,\,\,\vec{a}=a_t\vec{T}+a_n\vec{N}\,\,\longrightarrow\,\,|\,\vec{a}\,|=\sqrt{a_t^{\, 2}+a_n^{\, 2}}\,\right) | ||
</math></center> | </math></center> | ||
Otra posibilidad es calcular <math>\,a_n\,</math> proyectando <math>\,\vec{a}\,</math> sobre la dirección normal a <math>\,\vec{v}\,</math>: | |||
<center><math> | <center><math> | ||
a_n=\displaystyle\frac{|\,\vec{v}\times\vec{a}\,|}{v}=\frac{\sqrt{2}\,\rho_0\,c^{\, 2}}{1+c\,t} | |||
</math></center> | </math></center> | ||
El radio de curvatura <math>\,R_{\kappa}\,</math> de la trayectoria se obtiene a partir de <math>\,a_n\,</math> y de <math>\,v</math>: | |||
<center><math> | <center><math> | ||
R_{\kappa}=\displaystyle\frac{v^2}{a_n}=\sqrt{2}\,\rho_0\,(1+c\,t) | |||
</math></center> | </math></center> | ||
La potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula puede calcularse como derivada temporal de la energía cinética: | ==Vectores del triedro intrínseco== | ||
El vector tangente unitario <math>\,\vec{T}\,</math> se calcula normalizando la velocidad <math>\,\vec{v}</math>: | |||
<center><math> | |||
\vec{T}=\frac{\vec{v}}{v}=\frac{1}{\sqrt{2}}\,(\vec{u}_{\rho}+\vec{u}_{\theta}) | |||
</math></center> | |||
Al ser <math>\,a_t=0\,</math>, la aceleración <math>\,\vec{a}=a_n\vec{N}\,</math> tiene la dirección y el sentido del vector normal principal <math>\,\vec{N}\,</math>, y por ello <math>\,\vec{N}\,</math> se puede calcular normalizando <math>\,\vec{a}</math>: | |||
<center><math> | |||
\vec{N}=\frac{\vec{a}}{a_n}=\frac{1}{\sqrt{2}}\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta})\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(\mathrm{en}\,\,\mathrm{general,}\,\,\,\,\,\,\vec{N}=\frac{\vec{a}-a_t\vec{T}}{a_n}\,\right) | |||
</math></center> | |||
==Energía cinética y potencia instantánea. ¿Es la energía cinética una integral primera?== | |||
A partir de la celeridad <math>\,v\,</math>, calculada anteriormente, se obtiene la energía cinética <math>\,K\,</math> de la partícula: | |||
<center><math> | |||
K=\frac{1}{2}\,m v^{\, 2}=m\rho_0^2\,c^2 | |||
</math></center> | |||
Observamos que <math>\,K\,</math> permanece constante a lo largo del tiempo. Por tanto, la energía cinética es una integral primera del movimiento. | |||
La potencia instantánea <math>\,P\,</math> desarrollada por la fuerza neta que actúa sobre la partícula puede calcularse como la derivada temporal de la energía cinética: | |||
<center><math> | |||
P=\displaystyle\frac{dK}{dt}=0 | |||
</math></center> | |||
o bien puede calcularse también mediante el producto escalar de la fuerza neta <math>\,\vec{F}\,</math> por la velocidad <math>\,\vec{v}</math>: | |||
<center><math> | |||
P=\vec{F}\cdot\vec{v}=m\,\vec{a}\cdot\vec{v}=0 | |||
</math></center> | |||
Que la energía cinética sea una integral primera del movimiento guarda relación directa con el hecho de que la fuerza neta no desarrolle potencia sobre la partícula (teorema de conservación de la energía cinética). | |||
==Momento cinético respecto al punto O. ¿Se trata de un movimiento central con centro en O?== | |||
La partícula tendría un movimiento central con centro en el origen de coordenadas <math>\,O\,</math> si la fuerza neta que actúa sobre ella fuese paralela al vector de posición (<math>\vec{F}=m\,\vec{a}\,\parallel\,\vec{r}=\rho\,\vec{u}_{\rho}</math>), es decir, si la componente acimutal de la aceleración (<math>a_{\theta}</math>) fuese cero en todo instante de tiempo. Como esta nulidad no se cumple en el presente caso, el movimiento de la partícula no es central con centro en <math>\,O</math>: | |||
<center><math> | <center><math> | ||
a_{\theta}=\frac{\rho_0\,c^{\, 2}}{1+c\,t}\,\neq\,0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{no}\,\,\mathrm{es}\,\,\mathrm{movimiento}\,\,\mathrm{central}\,\,\mathrm{con}\,\,\mathrm{centro}\,\,\mathrm{en}\,\, O | |||
</math></center> | </math></center> | ||
Calculemos ahora el momento cinético <math>\,\vec{L}_O\,</math> de la partícula respecto al punto <math>O</math>: | |||
<center><math> | <center><math> | ||
\vec{L}_O=m\rho^{2}\dot{\theta}\,\,\vec{k}=m\rho_0^{2}c\,(1+\,c\,t)\,\,\vec{k} | |||
</math></center> | </math></center> | ||
Si la fuerza neta <math>\,\vec{F}\,</math> sobre la partícula <math>\,P\,</math> fuese central en <math>\,O\,</math>, el paralelismo <math>\,\vec{F}\parallel\overrightarrow{OP}\,</math> provocaría que el momento de fuerza <math>\,\vec{M}_O=\overrightarrow{OP}\times\vec{F}\,</math> fuese nulo y que, por tanto, el momento cinético <math>\,\vec{L}_O\,</math> fuese constante en el tiempo (teorema de conservación del momento cinético). Así, pues, el hecho de que el momento cinético <math>\,\vec{L}_O\,</math> haya resultado variable en el tiempo constituye una prueba alternativa de que el movimiento analizado no es central con centro en <math>\,O</math>: | |||
<center><math> | <center><math> | ||
\vec{L}_O\,\neq\,\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{no}\,\,\mathrm{es}\,\,\mathrm{movimiento}\,\,\mathrm{central}\,\,\mathrm{con}\,\,\mathrm{centro}\,\,\mathrm{en}\,\, O | |||
</math></center> | </math></center> | ||
[[Categoría:Problemas de Dinámica del Punto (GITI)]] | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión actual - 19:00 10 ene 2024
Enunciado
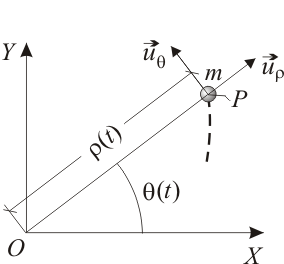
El movimiento de una partícula , de masa , en el plano queda descrito en coordenadas polares mediante las ecuaciones horarias:
siendo y constantes positivas conocidas.
- Determine la velocidad y la aceleración de la partícula (en la base polar ).
- Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria.
- Determine los vectores y del triedro intrínseco de la trayectoria de la partícula (en la base polar ).
- Calcule la energía cinética de la partícula, y la potencia desarrollada por la fuerza neta que actúa sobre ella. ¿Es la energía cinética una integral primera del movimiento?
- Calcule el momento cinético de la partícula respecto al punto ¿Es el movimiento de la partícula un movimiento central con centro en ? Razone la respuesta.
Velocidad y aceleración
La velocidad y la aceleración en componentes polares vienen dadas por las expresiones:
Necesitamos, por tanto, calcular las derivadas de primer y segundo orden de y respecto al tiempo:
y sustituyendo en las expresiones de y , se obtiene:
Componentes intrínsecas de la aceleración y radio de curvatura
Podemos calcular la aceleración tangencial como la derivada respecto al tiempo de la celeridad :
Otra posibilidad es calcular proyectando sobre la dirección de (que es tangente a la trayectoria):
Al ser , la aceleración normal coincide con el módulo del vector aceleración (recuérdese que siempre):
Otra posibilidad es calcular proyectando sobre la dirección normal a :
El radio de curvatura de la trayectoria se obtiene a partir de y de :
Vectores del triedro intrínseco
El vector tangente unitario se calcula normalizando la velocidad :
Al ser , la aceleración tiene la dirección y el sentido del vector normal principal , y por ello se puede calcular normalizando :
Energía cinética y potencia instantánea. ¿Es la energía cinética una integral primera?
A partir de la celeridad , calculada anteriormente, se obtiene la energía cinética de la partícula:
Observamos que permanece constante a lo largo del tiempo. Por tanto, la energía cinética es una integral primera del movimiento.
La potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula puede calcularse como la derivada temporal de la energía cinética:
o bien puede calcularse también mediante el producto escalar de la fuerza neta por la velocidad :
Que la energía cinética sea una integral primera del movimiento guarda relación directa con el hecho de que la fuerza neta no desarrolle potencia sobre la partícula (teorema de conservación de la energía cinética).
Momento cinético respecto al punto O. ¿Se trata de un movimiento central con centro en O?
La partícula tendría un movimiento central con centro en el origen de coordenadas si la fuerza neta que actúa sobre ella fuese paralela al vector de posición (), es decir, si la componente acimutal de la aceleración () fuese cero en todo instante de tiempo. Como esta nulidad no se cumple en el presente caso, el movimiento de la partícula no es central con centro en :
Calculemos ahora el momento cinético de la partícula respecto al punto :
Si la fuerza neta sobre la partícula fuese central en , el paralelismo provocaría que el momento de fuerza fuese nulo y que, por tanto, el momento cinético fuese constante en el tiempo (teorema de conservación del momento cinético). Así, pues, el hecho de que el momento cinético haya resultado variable en el tiempo constituye una prueba alternativa de que el movimiento analizado no es central con centro en :



















































