|
|
| Línea 1: |
Línea 1: |
| ==Enunciado== | | ==Enunciado== |
| [[Archivo:central-en-c.png|right]]
| | Una anilla, de dimensiones despreciables (considérese puntual) y de masa <math>2\,\,\mathrm{kg}\,</math>, desliza sin rozamiento a lo largo de un alambre rectilíneo en el que se halla ensartada. En cierto instante, se ha representado gráficamente la posición de la anilla, así como su aceleración (<math>\,\vec{a}\,\,</math>) y todas las fuerzas activas que soporta (<math>\vec{F}_1\,</math> y <math>\vec{F}_2\,</math>). Sin embargo, se ha dejado sin representar la fuerza de reacción vincular (<math>\vec{\Phi}\,</math>) que ejerce el alambre |
| | liso sobre la anilla. La cuadrícula de los diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial. |
|
| |
|
| Una partícula <math>P\,</math> de masa <math>m\,</math> se mueve en el plano <math>OXY\,</math>. Su trayectoria es la circunferencia de radio <math>R\,</math> y centro en el punto <math>O(0,0)\,</math>. La partícula soporta una única fuerza <math>\vec{F}\,</math>, cuya recta de acción pasa permanentemente por el punto <math>C(-R,0)\,</math>. Como parámetro descriptivo del movimiento, se utiliza el
| | ¿Cuál de los siguientes diagramas es el correcto? |
| ángulo <math>\theta(t)\,</math> de la figura, que satisface las condiciones iniciales <math>\theta(0)=0\,\,\,</math> y <math>\,\,\dot{\theta}(0)=\Omega\,</math>.
| | <center> |
| | [[Archivo:rectas-blanca.png]] |
| | </center> |
|
| |
|
| # Si <math>\vec{v}\,</math> es la velocidad instantánea de la partícula, ¿cuál de las siguientes magnitudes es una integral primera del movimiento de <math>P\,\,</math>? ('''NOTA''': sólo lo es una de las cuatro). <center><math>\mathrm{(a)}\,\,\,\, m\,\vec{v}\cdot\vec{v}/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(b)}\,\,\,\, \overrightarrow{OP}\times m\vec{v}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(c)}\,\,\,\, \overrightarrow{CP}\times m\vec{v}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(d)}\,\,\,\, m\vec{v}</math></center>
| | ==Solución== |
| # A partir de la integral primera del apartado anterior, deduzca la relación existente entre <math>\dot{\theta}\,</math> y <math>\theta\,</math> durante el movimiento.
| | Al deslizar a lo largo del alambre, la anilla realiza un movimiento rectilíneo, siendo sus vectores velocidad y aceleración necesariamente paralelos al propio alambre en todo instante. Así pues, se detecta a simple vista que el diagrama (3) es incorrecto por presentar un vector aceleración no paralelo al alambre. |
|
| |
|
| ==Integral primera==
| | Por otra parte, dice el enunciado que la única fuerza no representada en los diagramas es la fuerza de reacción vincular <math>\vec{\Phi}\,</math> ejercida por el alambre sobre la anilla. Pero esa fuerza vincular está relacionada con las fuerzas activas (sí representadas), y con la masa y la aceleración de la partícula, mediante la segunda ley de Newton: |
| Para saber cuál de las cuatro magnitudes propuestas es la que se conserva constante a lo largo del tiempo (integral primera), revisaremos los correspondientes teoremas de conservación hasta detectar cuál de ellos ve sus requisitos satisfechos en el caso que nos ocupa.
| |
| | |
| Comenzaremos descartando la opción (d). Según el teorema de conservación de la cantidad de movimiento de una partícula, la magnitud <math>\vec{p}=m\vec{v}\,</math> sólo mantiene su valor constante en el tiempo si la fuerza neta que actúa sobre la partícula es nula. Pero esto no ocurre en el caso presente, ya que la fuerza <math>\vec{F}\,</math> (única existente) no es nula:
| |
| <center><math> | | <center><math> |
| \frac{d\vec{p}}{dt}=\vec{F}\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,
| | \vec{F}_1\,+\,\vec{F}_2\,+\,\vec{\Phi}=m\vec{a} |
| \vec{p}=m\vec{v}\neq\overrightarrow{\mathrm{cte}} | |
| </math></center> | | </math></center> |
| Descartamos ahora la opción (a). Conforme al teorema de conservación de la energía cinética de una partícula, la magnitud <math>K=m\,\vec{v}\cdot\vec{v}/2\,</math> sólo mantiene su valor constante en el tiempo si el trabajo neto realizado sobre la partícula es nulo (<math>\delta W=0\,</math>). Sin embargo, la fuerza <math>\vec{F}\,</math> descrita en el enunciado no es ortogonal a la trayectoria de la partícula (no tiene dirección radial) y, por tanto, trabaja:
| | Dado que no existe rozamiento entre la anilla y el alambre (vínculo liso), sabemos que <math>\vec{\Phi}\,</math> no tiene componente paralela al alambre. Por tanto, si definimos un eje OX en la dirección longitudinal del alambre (sentido hacia la derecha) y proyectamos la ecuación de la segunda ley de Newton sobre dicho eje (multiplicándola escalarmente por el vector <math>\vec{\imath}\,</math>), lograremos que la fuerza de reacción vincular desaparezca: |
| <center><math> | | <center><math> |
| dK=\delta W=\vec{F}\cdot d\vec{r}\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,K=m\,\vec{v}\cdot\vec{v}/2\neq\mathrm{cte}
| | \vec{F}_1\,\cdot\vec{\imath}\,+\,\vec{F}_2\,\cdot\vec{\imath}\,+\,\underbrace{\vec{\Phi}\,\cdot\vec{\imath}}_{=0}=m\vec{a}\,\cdot\vec{\imath}\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,F_{1x}\,+\,F_{2x}=ma_x |
| </math></center> | | </math></center> |
| Y descartamos también la opción (b). El teorema de conservación del momento cinético de una partícula respecto a un punto fijo establece que la magnitud <math>\vec{L}_O=\overrightarrow{OP}\times m\vec{v}\,</math> sólo mantiene su valor constante en el tiempo si es nulo el momento resultante <math>\vec{M}_O\,</math> de las fuerzas que actúan sobre la partícula. En el caso que nos ocupa, el momento <math>\overrightarrow{M}_O\,</math> es distinto de cero debido a que la recta de acción de la fuerza <math>\vec{F}\,</math> no pasa en general por el punto <math>O\,</math> (es decir, <math>\vec{F}\,</math> no es una fuerza central con centro en <math>O\,</math>):
| | La masa de la anilla es <math>m=2\,\,\mathrm{kg}\,</math>, y la cuadrícula de los diagramas nos permite conocer los valores numéricos de las componentes-x de los vectores representados. Así que podemos determinar cuál es el diagrama correcto (de entre los aún no descartados) comprobando en cuál de ellos se verifica la ecuación <math>F_{1x}\,+\,F_{2x}=ma_x\,</math>: |
| <center><math> | | <center><math> |
| \frac{d\vec{L}_O}{dt}=\overrightarrow{M}_O=\overrightarrow{OP}\,\times \vec{F}\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\, | | \begin{array}{lll} |
| \vec{L}_O=\overrightarrow{OP}\times m\vec{v}\neq\overrightarrow{\mathrm{cte}} | | \mathrm{diagrama}\,\,1\,\,(\,F_{1x}=3\,\mathrm{N}\,,\,\,\, F_{2x}=1\,\mathrm{N}\,,\,\,\, a_x=3\,\mathrm{m}/\mathrm{s}^2\,,\,\,\,ma_x=6\,\mathrm{N}\,) & \,\,\longrightarrow\,\, & F_{1x}+F_{2x}=(\,3+1\,)\, \mathrm{N}\neq 6\,\mathrm{N}= ma_x \\ \\ |
| | \mathrm{diagrama}\,\,2\,\,(\,F_{1x}=4\,\mathrm{N}\,,\,\,\, F_{2x}=-\,2\,\mathrm{N}\,,\,\,\, a_x=2\,\mathrm{m}/\mathrm{s}^2\,,\,\,\,ma_x=4\,\mathrm{N}\,) & \,\,\longrightarrow\,\, & F_{1x}+F_{2x}=(\,4-2\,)\, \mathrm{N}\neq 4\,\mathrm{N}= ma_x \\ \\ |
| | \mathrm{diagrama}\,\,4 \,\,(\,F_{1x}=0\,\mathrm{N}\,,\,\,\, F_{2x}=-\,4\,\mathrm{N}\,,\,\,\, a_x=-\,2\,\mathrm{m}/\mathrm{s}^2\,,\,\,\,ma_x=-\,4\,\mathrm{N}\,) & \,\,\longrightarrow\,\, & F_{1x}+F_{2x}=(\,0-4\,)\, \mathrm{N}= -\,4\,\mathrm{N}= ma_x |
| | \end{array} |
| </math></center> | | </math></center> |
| Descartadas ya tres opciones, sólo resta comprobar que la opción (c) es la correcta. Para ello, basta aplicar de nuevo el teorema de conservación del momento cinético de una partícula, pero referido esta vez al punto fijo <math>C\,</math>. La magnitud <math>\vec{L}_C=\overrightarrow{CP}\times m\vec{v}\,</math> sólo mantiene su valor constante en el tiempo si es nulo el momento resultante <math>\vec{M}_C\,</math> de las fuerzas que actúan sobre la partícula. Y así ocurre en efecto en el caso que nos ocupa, la fuerza <math>\vec{F}\,</math> tiene momento nulo respecto al punto <math>C\,</math> debido a que su recta de acción pasa permanentemente por dicho punto (es decir, <math>\vec{F}\,</math> es una fuerza central con centro en <math>C\,</math>):
| | Concluimos que el diagrama (4) es el correcto. |
| <center><math>
| | |
| \frac{d\vec{L}_C}{dt}=\overrightarrow{M}_C=\overrightarrow{CP}\,\times \vec{F}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,
| | [[Categoría: Problemas de Dinámica del Punto (GITI)]] |
| \vec{L}_C=\overrightarrow{CP}\times m\vec{v}=\overrightarrow{\mathrm{cte}}
| |
| </math></center>
| |
| Por tanto, queda comprobado que, de las cuatro magnitudes que se propusieron en el enunciado, la única que necesariamente se conserva constante a lo largo del tiempo (integral primera) es el momento cinético de la partícula respecto al punto <math>C\,</math>, es decir, <math>\overrightarrow{CP}\times m\vec{v}\,</math>.
| |
| | |
| ==Relación existente entre <math>\dot{\theta}\,</math> y <math>\theta\,</math> durante el movimiento==
| |
| Una vez sabido que el momento cinético de la partícula respecto al punto <math>C\,</math> es una integral primera, procedemos a determinar su expresión en función de <math>\dot{\theta}\,</math> y <math>\theta\,</math>:
| |
| <center><math>
| |
| \left.\begin{array}{l}
| |
| \overrightarrow{OP}=\vec{r}=R\,[\,\mathrm{cos}(\theta)\,\vec{\imath}+\mathrm{sen}(\theta)\,\vec{\jmath}\,\,]\,\,;\,\,\,\,\,\overrightarrow{OC}=-R\,\vec{\imath} \\ \\
| |
| \overrightarrow{CP}=\overrightarrow{OP}-\overrightarrow{OC}=R\,\{[1+\mathrm{cos}(\theta)]\,\vec{\imath}+\mathrm{sen}(\theta)\,\vec{\jmath}\,\} \\ \\
| |
| \vec{v}=\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\dot{\theta}\,\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=R\,\dot{\theta}\,[-\,\mathrm{sen}(\theta)\,\vec{\imath}+\mathrm{cos}(\theta)\,\vec{\jmath}\,\,]
| |
| \end{array}\right\}
| |
| \,\,\,\,\,\longrightarrow\,\,\,\,\,
| |
| \overrightarrow{CP}\,\times\, m\vec{v}=mR^2\dot{\theta}\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 1+\mathrm{cos}(\theta) & \mathrm{sen}(\theta) & 0 \\ -\mathrm{sen}(\theta) & \mathrm{cos}(\theta) & 0 \end{array}\right|=mR^2\dot{\theta}\,[1+\,\mathrm{cos}(\theta)]\,\vec{k}
| |
| </math></center>
| |
| Y, a continuación, determinamos su valor constante a partir de las condiciones iniciales, lo cual nos permite a su vez deducir la relación existente entre <math>\dot{\theta}\,</math> y <math>\theta\,</math> durante el movimiento:
| |
| <center><math>
| |
| \left.\begin{array}{l}
| |
| \theta(0)=0 \\
| |
| \dot{\theta}(0)=\Omega
| |
| \end{array}\right\}
| |
| \,\,\,\,\,\longrightarrow\,\,\,\,\,
| |
| mR^2\dot{\theta}\,[1+\,\mathrm{cos}(\theta)]\,\vec{k}=mR^2\Omega\,[1+\,\mathrm{cos}(0)]\,\vec{k}=2\,mR^2\Omega\,\vec{k}
| |
| \,\,\,\,\,\Rightarrow\,\,\,\,\,\dot{\theta}\,[1+\,\mathrm{cos}(\theta)]=2\,\Omega\,\,\,\,\,\Rightarrow\,\,\,\,\,\dot{\theta}=\frac{2\,\Omega}{1+\mathrm{cos}(\theta)}
| |
| </math></center>
| |
| | |
| [[Categoría:Problemas de Dinámica del Punto (GITI)]] | |
Enunciado
Una anilla, de dimensiones despreciables (considérese puntual) y de masa  , desliza sin rozamiento a lo largo de un alambre rectilíneo en el que se halla ensartada. En cierto instante, se ha representado gráficamente la posición de la anilla, así como su aceleración (
, desliza sin rozamiento a lo largo de un alambre rectilíneo en el que se halla ensartada. En cierto instante, se ha representado gráficamente la posición de la anilla, así como su aceleración ( ) y todas las fuerzas activas que soporta (
) y todas las fuerzas activas que soporta ( y
y  ). Sin embargo, se ha dejado sin representar la fuerza de reacción vincular (
). Sin embargo, se ha dejado sin representar la fuerza de reacción vincular ( ) que ejerce el alambre
liso sobre la anilla. La cuadrícula de los diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial.
) que ejerce el alambre
liso sobre la anilla. La cuadrícula de los diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial.
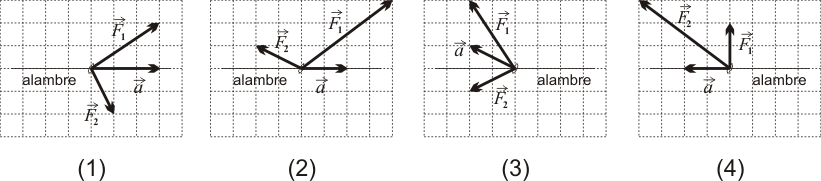
¿Cuál de los siguientes diagramas es el correcto?
Solución
Al deslizar a lo largo del alambre, la anilla realiza un movimiento rectilíneo, siendo sus vectores velocidad y aceleración necesariamente paralelos al propio alambre en todo instante. Así pues, se detecta a simple vista que el diagrama (3) es incorrecto por presentar un vector aceleración no paralelo al alambre.
Por otra parte, dice el enunciado que la única fuerza no representada en los diagramas es la fuerza de reacción vincular  ejercida por el alambre sobre la anilla. Pero esa fuerza vincular está relacionada con las fuerzas activas (sí representadas), y con la masa y la aceleración de la partícula, mediante la segunda ley de Newton:
ejercida por el alambre sobre la anilla. Pero esa fuerza vincular está relacionada con las fuerzas activas (sí representadas), y con la masa y la aceleración de la partícula, mediante la segunda ley de Newton:

Dado que no existe rozamiento entre la anilla y el alambre (vínculo liso), sabemos que  no tiene componente paralela al alambre. Por tanto, si definimos un eje OX en la dirección longitudinal del alambre (sentido hacia la derecha) y proyectamos la ecuación de la segunda ley de Newton sobre dicho eje (multiplicándola escalarmente por el vector
no tiene componente paralela al alambre. Por tanto, si definimos un eje OX en la dirección longitudinal del alambre (sentido hacia la derecha) y proyectamos la ecuación de la segunda ley de Newton sobre dicho eje (multiplicándola escalarmente por el vector  ), lograremos que la fuerza de reacción vincular desaparezca:
), lograremos que la fuerza de reacción vincular desaparezca:

La masa de la anilla es  , y la cuadrícula de los diagramas nos permite conocer los valores numéricos de las componentes-x de los vectores representados. Así que podemos determinar cuál es el diagrama correcto (de entre los aún no descartados) comprobando en cuál de ellos se verifica la ecuación
, y la cuadrícula de los diagramas nos permite conocer los valores numéricos de las componentes-x de los vectores representados. Así que podemos determinar cuál es el diagrama correcto (de entre los aún no descartados) comprobando en cuál de ellos se verifica la ecuación  :
:

Concluimos que el diagrama (4) es el correcto.











