Diferencia entre las páginas «No Boletín - Cuestión sobre curva de potencial VII (Ex.Ene/20)» y «No Boletín - Cuestión sobre integral primera (Ex.Ene/13)»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo: | [[Archivo:esfera.png|right]] | ||
En el sistema de referencia <math>OXYZ\,</math> de la figura, la partícula <math>P\,</math> se mueve bajo la acción de su propio peso y | |||
vinculada sin rozamiento a una superficie esférica fija de radio <math>R\,</math> y centro en el punto <math>O\,</math> (la ecuación de ligadura es <math>x^{2}+y^{2}+z^{2}=R^{2}\,</math>). | |||
¿Cuál de las siguientes magnitudes físicas de la partícula <math>P\,</math> se conserva necesariamente constante durante el movimiento? ('''NOTA''': sólo una de las cuatro opciones es correcta). | |||
(a) La componente-<math>z\,</math> de su momento cinético respecto al punto <math>O\,</math> | |||
(b) Su cantidad de movimiento | |||
(c) Su energía cinética | |||
(d) Su momento cinético respecto al punto <math>O\,</math> | |||
==Solución== | |||
[[Archivo:esfera-sol.png|right]] | |||
Para saber cuál de las cuatro magnitudes propuestas es la que se conserva constante a lo largo del tiempo (integral primera), debemos examinar, en primer lugar, qué fuerzas actúan sobre la partícula y qué características tienen dichas fuerzas. Y, después, tendremos que ir revisando los teoremas de conservación asociados a las magnitudes propuestas hasta detectar cuál de ellos ve sus requisitos satisfechos en el caso que nos ocupa. | |||
Las fuerzas que actúan sobre la partícula son dos: el peso (<math>m\vec{g}\,</math>) y la fuerza de reacción vincular (<math>\vec{\Phi}\,</math>) ejercida por la superficie esférica. | |||
El peso es una fuerza activa y, como tal, conocida a priori: | |||
<center><math> | |||
m\vec{g}=-mg\,\vec{k} | |||
</math></center> | |||
Sabemos, además, que el peso es una fuerza conservativa, y que va a realizar trabajo sobre la partícula porque en general la coordenada-<math>z\,</math> de ésta no va a permanecer constante durante su movimiento. | |||
En cuanto a la fuerza de reacción vincular <math>\vec{\Phi}\,</math>, no conocemos a priori su módulo ni su sentido, pero sabemos que su dirección ha de ser perpendicular a la superficie esférica (al ser ésta un vínculo liso o sin rozamiento) y, por tanto, es radial. La expresaremos así: | |||
<center><math> | |||
\vec{\Phi}=\lambda\,\overrightarrow{OP}=\lambda\,(x\,\vec{\imath}+y\,\vec{\jmath}+z\,\vec{k}\,)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(}\lambda=\,\mathrm{incognita}\,\,\mathrm{escalar}\,\mathrm{)} | |||
</math></center> | |||
También sabemos que <math>\vec{\Phi}\,</math> es una fuerza que no va a realizar trabajo, ya que el vínculo -además de liso- es esclerónomo o fijo y, por tanto, la trayectoria de la partícula va a ser siempre perpendicular a <math>\vec{\Phi}\,</math>. En efecto: | |||
<center><math> | |||
\vec{\Phi}\,\cdot\,d\vec{r}=\lambda\,(x\,\vec{\imath}\,+\,y\,\vec{\jmath}\,+\,z\,\vec{k}\,)\,\cdot\,(dx\,\vec{\imath}\,+\,dy\,\vec{\jmath}\,+\,dz\,\vec{k}\,)=\lambda\,(x\, dx\,+\,y\, dy\,+\,z\, dz)=\frac{\lambda}{2}\,d(x^{2}+y^{2}+z^{2})=\frac{\lambda}{2}\,d(R^{2})=0 | |||
</math></center> | |||
==Descartando la opción (b)== | |||
Según el correspondiente teorema de conservación, la cantidad de movimiento <math>\vec{p}\,</math> de la partícula se conservaría constante si y sólo si la fuerza neta <math>\vec{F}\,</math> que actúa sobre la partícula fuese nula. Pero esto no ocurre aquí, ya que <math>\vec{\Phi}\,</math> (de dirección radial) y <math>m\vec{g}\,</math> (de dirección vertical) no pueden en general cancelarse mutuamente. En efecto: | |||
<center><math> | |||
\frac{d\vec{p}}{dt}=\vec{F}=m\vec{g}+\vec{\Phi}=\lambda\,x\,\vec{\imath}+\lambda\,y\,\vec{\jmath}+(\lambda\,z-mg)\,\vec{k}\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\, | |||
\vec{p}\neq\overrightarrow{\mathrm{cte}} | |||
</math></center> | |||
'''Nota''': Obsérvese que, dada una posición arbitraria de la partícula sobre la esfera, no existe ninguna solución en <math>\lambda\,</math> para la cual se anulen simultáneamente las tres componentes de <math>\vec{F}\,</math>. | |||
==Descartando la opción (c)== | |||
Conforme al correspondiente teorema de conservación, para que se conservase constante la energía cinética <math>K\,</math> de la partícula sería necesario y suficiente que no se realizase trabajo neto sobre la partícula (<math>\delta W=0\,</math>). Sin embargo, en el caso que nos ocupa, si bien es cierto que <math>\vec{\Phi}\,</math> no trabaja, el peso sí que trabaja puesto que la coordenada-<math>z\,</math> de la partícula es variable (<math>dz\neq 0\,</math>). En efecto: | |||
<center><math> | <center><math> | ||
\ | dK=\delta W=\vec{F}\,\cdot\, d\vec{r}=(m\vec{g}\,+\,\vec{\Phi})\,\cdot\, d\vec{r}=m\vec{g}\,\cdot\, d\vec{r}\,+\,\underbrace{\vec{\Phi}\cdot d\vec{r}}_{=0}=-mg\,\vec{k}\,\cdot\,(dx\,\vec{\imath}\,+\,dy\,\vec{\jmath}\,+\,dz\,\vec{k}\,)=-mg\,dz\neq 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,K\neq\mathrm{cte} | ||
\,\ | |||
</math></center> | </math></center> | ||
y | |||
==Descartando la opción (d)== | |||
El teorema de conservación del momento cinético <math>\vec{L}_O\,</math> de una partícula establece que dicha magnitud se conserva constante en el tiempo si y sólo si es nulo el momento resultante <math>\vec{M}_O\,</math> de las fuerzas que actúan sobre la partícula. En el caso que nos ocupa, <math>\vec{\Phi}\,</math> tiene momento nulo respecto a <math>O\,</math> debido a su dirección radial. Pero, sin embargo, el momento (respecto a <math>O\,</math>) del peso es distinto de cero en general. En efecto: | |||
<center><math> | <center><math> | ||
\ | \frac{d\vec{L}_O}{dt}=\vec{M}_O=\overrightarrow{OP}\,\times \vec{F}=\overrightarrow{OP}\,\times\,(m\vec{g}\,+\,\vec{\Phi}\,)=\overrightarrow{OP}\,\times (-mg\,\vec{k}\,)\,+\,\underbrace{\overrightarrow{OP}\times\lambda\,\overrightarrow{OP}}_{=\vec{0}}=mg\,(-y\,\vec{\imath}\,+\,x\,\vec{\jmath}\,)\neq\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\, | ||
\,\,\,\ | \vec{L}_O\neq\overrightarrow{\mathrm{cte}} | ||
</math></center> | </math></center> | ||
== | ==Eligiendo la opción (a)== | ||
Descartadas ya tres opciones, sólo resta comprobar que la opción (a) es la correcta. ¿Qué hace falta, según el correspondiente teorema de conservación, para que se conserve constante la componente-<math>z\,</math> de <math>\vec{L}_O\,</math>? Respuesta: hace falta la nulidad de la componente-<math>z\,</math> de <math>\vec{M}_O\,</math>. | |||
Multiplicando escalarmente la expresión ya obtenida de <math>\vec{M}_O\,</math> por <math>\vec{k}\,</math>, obtendremos la componente-<math>z\,</math> de dicho vector. Aunque, en realidad, basta observar la expresión de <math>\vec{M}_O\,</math> para darse cuenta de que es nula su componente-<math>z\,</math>. En efecto: | |||
<center><math> | |||
\frac{d(\vec{k}\cdot\vec{L}_O)}{dt}=\vec{k}\cdot\vec{M}_O=\vec{k}\,\cdot\, mg\,(-y\,\vec{\imath}\,+\,x\,\vec{\jmath}\,)=0\,\,\,\,\,\Longrightarrow\,\,\,\,\, | |||
\vec{k}\cdot\vec{L}_O=\mathrm{cte} | |||
</math></center> | |||
Por tanto, queda comprobado que, de las cuatro magnitudes que se propusieron en el enunciado, la única que necesariamente se conserva constante a lo largo del tiempo (integral primera) es la componente-<math>z\,</math> del momento cinético de la partícula respecto al punto <math>O\,</math>. | |||
==Conservación de la energía mecánica== | |||
En la situación planteada, cabe señalar que el movimiento de la partícula tiene otra integral primera además de la ya determinada. Lo que ocurre es que esa otra integral primera no estaba entre las cuatro opciones que se propusieron en el enunciado. Se trata de la energía mecánica de la partícula (suma de la energía cinética y la energía potencial asociada al peso). Se cumple la condición establecida por el correspondiente teorema de conservación: que todas las fuerzas que trabajen sobre la partícula sean conservativas (aquí sólo trabaja el peso, que es en efecto conservativo). Así pues, la energía mecánica de la partícula también se conserva constante a lo largo del tiempo. | |||
De hecho, en un examen posterior (Septiembre/2014) se propuso una sutil variante de esta misma cuestión, en la cual sólo se modificaron dos elementos: se sustituyó la opción-respuesta "Su energía cinética" por "Su energía mecánica", y se cambió la orientación del sistema de referencia OXYZ de modo que el eje OY pasó a ser el eje vertical (paralelo a la gravedad) en lugar del eje OZ. Obviamente, la respuesta correcta en esta variante de la cuestión pasó a ser "Su energía mecánica". Muchos alumnos, sin embargo, guiados por su "memoria" y por su falta de atención a los detalles, creyeron que la componente-z del momento cinético respecto al punto O se conservaba constante, lo cual no era cierto porque el cambio de eje vertical conllevaba que ahora se conservase constante la componente-y (en lugar de la componente-z) del citado momento cinético. | |||
[[Categoría:Problemas de Dinámica del Punto (GITI)]] | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión del 18:57 10 ene 2024
Enunciado
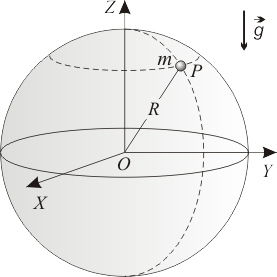
En el sistema de referencia de la figura, la partícula se mueve bajo la acción de su propio peso y vinculada sin rozamiento a una superficie esférica fija de radio y centro en el punto (la ecuación de ligadura es ).
¿Cuál de las siguientes magnitudes físicas de la partícula se conserva necesariamente constante durante el movimiento? (NOTA: sólo una de las cuatro opciones es correcta).
(a) La componente- de su momento cinético respecto al punto
(b) Su cantidad de movimiento
(c) Su energía cinética
(d) Su momento cinético respecto al punto
Solución
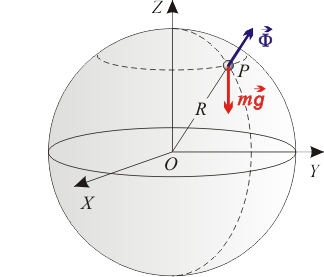
Para saber cuál de las cuatro magnitudes propuestas es la que se conserva constante a lo largo del tiempo (integral primera), debemos examinar, en primer lugar, qué fuerzas actúan sobre la partícula y qué características tienen dichas fuerzas. Y, después, tendremos que ir revisando los teoremas de conservación asociados a las magnitudes propuestas hasta detectar cuál de ellos ve sus requisitos satisfechos en el caso que nos ocupa.
Las fuerzas que actúan sobre la partícula son dos: el peso () y la fuerza de reacción vincular () ejercida por la superficie esférica.
El peso es una fuerza activa y, como tal, conocida a priori:
Sabemos, además, que el peso es una fuerza conservativa, y que va a realizar trabajo sobre la partícula porque en general la coordenada- de ésta no va a permanecer constante durante su movimiento.
En cuanto a la fuerza de reacción vincular , no conocemos a priori su módulo ni su sentido, pero sabemos que su dirección ha de ser perpendicular a la superficie esférica (al ser ésta un vínculo liso o sin rozamiento) y, por tanto, es radial. La expresaremos así:
También sabemos que es una fuerza que no va a realizar trabajo, ya que el vínculo -además de liso- es esclerónomo o fijo y, por tanto, la trayectoria de la partícula va a ser siempre perpendicular a . En efecto:
Descartando la opción (b)
Según el correspondiente teorema de conservación, la cantidad de movimiento de la partícula se conservaría constante si y sólo si la fuerza neta que actúa sobre la partícula fuese nula. Pero esto no ocurre aquí, ya que (de dirección radial) y (de dirección vertical) no pueden en general cancelarse mutuamente. En efecto:
Nota: Obsérvese que, dada una posición arbitraria de la partícula sobre la esfera, no existe ninguna solución en para la cual se anulen simultáneamente las tres componentes de .
Descartando la opción (c)
Conforme al correspondiente teorema de conservación, para que se conservase constante la energía cinética de la partícula sería necesario y suficiente que no se realizase trabajo neto sobre la partícula (). Sin embargo, en el caso que nos ocupa, si bien es cierto que no trabaja, el peso sí que trabaja puesto que la coordenada- de la partícula es variable (). En efecto:
Descartando la opción (d)
El teorema de conservación del momento cinético de una partícula establece que dicha magnitud se conserva constante en el tiempo si y sólo si es nulo el momento resultante de las fuerzas que actúan sobre la partícula. En el caso que nos ocupa, tiene momento nulo respecto a debido a su dirección radial. Pero, sin embargo, el momento (respecto a ) del peso es distinto de cero en general. En efecto:
Eligiendo la opción (a)
Descartadas ya tres opciones, sólo resta comprobar que la opción (a) es la correcta. ¿Qué hace falta, según el correspondiente teorema de conservación, para que se conserve constante la componente- de ? Respuesta: hace falta la nulidad de la componente- de .
Multiplicando escalarmente la expresión ya obtenida de por , obtendremos la componente- de dicho vector. Aunque, en realidad, basta observar la expresión de para darse cuenta de que es nula su componente-. En efecto:
Por tanto, queda comprobado que, de las cuatro magnitudes que se propusieron en el enunciado, la única que necesariamente se conserva constante a lo largo del tiempo (integral primera) es la componente- del momento cinético de la partícula respecto al punto .
Conservación de la energía mecánica
En la situación planteada, cabe señalar que el movimiento de la partícula tiene otra integral primera además de la ya determinada. Lo que ocurre es que esa otra integral primera no estaba entre las cuatro opciones que se propusieron en el enunciado. Se trata de la energía mecánica de la partícula (suma de la energía cinética y la energía potencial asociada al peso). Se cumple la condición establecida por el correspondiente teorema de conservación: que todas las fuerzas que trabajen sobre la partícula sean conservativas (aquí sólo trabaja el peso, que es en efecto conservativo). Así pues, la energía mecánica de la partícula también se conserva constante a lo largo del tiempo.
De hecho, en un examen posterior (Septiembre/2014) se propuso una sutil variante de esta misma cuestión, en la cual sólo se modificaron dos elementos: se sustituyó la opción-respuesta "Su energía cinética" por "Su energía mecánica", y se cambió la orientación del sistema de referencia OXYZ de modo que el eje OY pasó a ser el eje vertical (paralelo a la gravedad) en lugar del eje OZ. Obviamente, la respuesta correcta en esta variante de la cuestión pasó a ser "Su energía mecánica". Muchos alumnos, sin embargo, guiados por su "memoria" y por su falta de atención a los detalles, creyeron que la componente-z del momento cinético respecto al punto O se conservaba constante, lo cual no era cierto porque el cambio de eje vertical conllevaba que ahora se conservase constante la componente-y (en lugar de la componente-z) del citado momento cinético.























