Diferencia entre las páginas «No Boletín - Cuestión sobre curva de potencial VI (Ex.Ene/16)» y «No Boletín - Cuestión sobre curva de potencial VII (Ex.Ene/20)»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo: | [[Archivo:curva-potencial-ampli.png|right]] | ||
Una partícula | Una partícula se mueve en el eje <math>\,OX\,</math> bajo la acción de una fuerza conservativa. La función energía potencial <math>U(x)\,</math> y el nivel de energía mecánica <math>E\,</math> de la partícula son los representados en la gráfica adjunta. La partícula se halla inicialmente en la posición <math>\,x=x_0\,</math> (ver gráfica), que corresponde a uno de los puntos de corte de <math>E\,</math> y <math>U(x)\,</math>. | ||
¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento? | |||
==Regiones prohibidas y regiones permitidas== | |||
[[Archivo:sol-curva-2020.png|right]] | |||
Los puntos de retorno corresponden a los valores de <math>\,x\,</math> para los cuales se produce intersección entre la curva de energía potencial <math>\,U(x)\,</math> y la recta horizontal representativa de la energía mecánica constante <math>E\,</math>. Observamos en la gráfica que existen cuatro puntos de retorno: A, C, D y G. | |||
Los puntos de retorno corresponden a los valores de <math>\,x\,</math> para los cuales se produce intersección entre la curva de energía potencial <math>\,U(x)\,</math> y la recta horizontal representativa de la energía mecánica constante <math>E\,</math>. Observamos en la gráfica que existen | |||
Se denominan "de retorno" porque, si la partícula llega a uno de estos puntos, sufrirá allí la anulación instantánea de su celeridad y la inversión del sentido de su movimiento. Esta inversión del sentido de movimiento se debe a que cada punto de retorno es la frontera entre una región permitida y una región prohibida. | Se denominan "de retorno" porque, si la partícula llega a uno de estos puntos, sufrirá allí la anulación instantánea de su celeridad y la inversión del sentido de su movimiento. Esta inversión del sentido de movimiento se debe a que cada punto de retorno es la frontera entre una región permitida y una región prohibida. | ||
| Línea 25: | Línea 15: | ||
En efecto, la energía cinética de una partícula es, por definición, mayor o igual que cero (no negativa) y, por tanto, la partícula tiene prohibido su acceso a aquellas regiones del eje <math>\,OX\,</math> para las cuales la curva de energía potencial <math>\,U(x)\,</math> está por encima de la recta horizontal de energía mecánica <math>E\,</math>. | En efecto, la energía cinética de una partícula es, por definición, mayor o igual que cero (no negativa) y, por tanto, la partícula tiene prohibido su acceso a aquellas regiones del eje <math>\,OX\,</math> para las cuales la curva de energía potencial <math>\,U(x)\,</math> está por encima de la recta horizontal de energía mecánica <math>E\,</math>. | ||
En el caso que nos ocupa, detectamos | En el caso que nos ocupa, detectamos tres regiones prohibidas, que son la región a la izquierda del punto A, la región comprendida entre los puntos C y D, y la región a la derecha del punto G: | ||
<center><math> | <center><math> | ||
x_{\mathrm{C}}<x<x_{\mathrm{ | \left.\begin{array}{l} x< x_{\mathrm{A}} \\ \\ x_{\mathrm{C}}<x<x_{\mathrm{D}} \\ \\ x_{\mathrm{G}}< x \end{array}\right\} | ||
\,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{1}{2}m\dot{x}^{\, 2}=K=E-\,U(x)<0\,\,\,\,\mathrm{(imposible)}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{ | \,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{1}{2}m\dot{x}^{\, 2}=K=E-\,U(x)<0\,\,\,\,\mathrm{(imposible)}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{regiones}\,\,\mathrm{prohibidas} | ||
</math></center> | </math></center> | ||
y dos regiones permitidas, que son la región | y dos regiones permitidas, que son la región comprendida entre los puntos A y C, y la región comprendida entre los puntos D y G: | ||
<center><math> | <center><math> | ||
\left.\begin{array}{l} x\le x_{\mathrm{C}} \\ \\ x_{\mathrm{ | \left.\begin{array}{l} x_{\mathrm{A}}\le x \le x_{\mathrm{C}} \\ \\ x_{\mathrm{D}}\le x \le x_{\mathrm{G}} \end{array}\right\} | ||
\,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{1}{2}m\dot{x}^{\, 2}=K=E-\,U(x)\ge 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{regiones}\,\,\mathrm{permitidas} | \,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{1}{2}m\dot{x}^{\, 2}=K=E-\,U(x)\ge 0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{regiones}\,\,\mathrm{permitidas} | ||
</math></center> | </math></center> | ||
Nótese que, al ser las dos regiones permitidas no conexas entre sí (están separadas por | Nótese que, al ser las dos regiones permitidas no conexas entre sí (están separadas por una región prohibida o barrera de potencial), el movimiento de la partícula transcurrirá ''de facto'' sólo en una de las dos regiones permitidas. Pero ¿en cuál de las dos? Pues en aquella región en la que se halle la partícula inicialmente. En el presente caso, la posición inicial <math>\,x=x_0\,</math> de la partícula corresponde al punto G. Por tanto, la partícula se moverá siempre confinada en la región comprendida entre los puntos D y G, ya que la barrera de potencial a la izquierda de D convierte a la otra región permitida en inaccesible ''de facto''. | ||
==Posiciones de equilibrio | ==Posiciones de equilibrio== | ||
En el movimiento unidimensional conservativo de una partícula, las posiciones de equilibrio se corresponden con los extremos locales de la función energía potencial (máximos <math>\,\rightarrow\,</math> equilibrio inestable; mínimos <math>\,\rightarrow\,</math> equilibrio estable). En el caso que nos ocupa, observamos que la curva <math>U(x)\,</math> tiene dos mínimos (en B y en F) y un máximo (en O). Hay, por tanto, tres posiciones de equilibrio (B, O y F). | |||
Sin embargo, la pregunta exacta que se nos formula en este ejercicio es: ¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento? | |||
Pues bien, la respuesta correcta es UNA (en concreto, F). Porque, teniendo el nivel de energía mecánica <math>E\,</math> representado en la gráfica, resulta imposible para la partícula pasar por los puntos O (por quedar dentro de una región prohibida) y B (por quedar dentro de una región permitida pero inaccesible "de facto"). | |||
[[Categoría:Problemas de Dinámica del Punto (GITI)]] | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión actual - 18:57 10 ene 2024
Enunciado
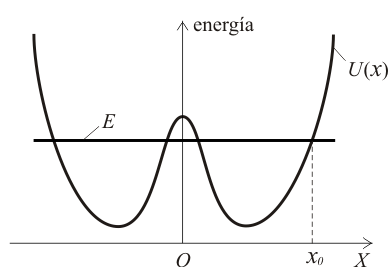
Una partícula se mueve en el eje bajo la acción de una fuerza conservativa. La función energía potencial y el nivel de energía mecánica de la partícula son los representados en la gráfica adjunta. La partícula se halla inicialmente en la posición (ver gráfica), que corresponde a uno de los puntos de corte de y .
¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento?
Regiones prohibidas y regiones permitidas
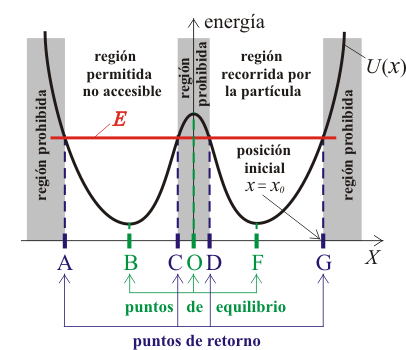
Los puntos de retorno corresponden a los valores de para los cuales se produce intersección entre la curva de energía potencial y la recta horizontal representativa de la energía mecánica constante . Observamos en la gráfica que existen cuatro puntos de retorno: A, C, D y G.
Se denominan "de retorno" porque, si la partícula llega a uno de estos puntos, sufrirá allí la anulación instantánea de su celeridad y la inversión del sentido de su movimiento. Esta inversión del sentido de movimiento se debe a que cada punto de retorno es la frontera entre una región permitida y una región prohibida.
En efecto, la energía cinética de una partícula es, por definición, mayor o igual que cero (no negativa) y, por tanto, la partícula tiene prohibido su acceso a aquellas regiones del eje para las cuales la curva de energía potencial está por encima de la recta horizontal de energía mecánica .
En el caso que nos ocupa, detectamos tres regiones prohibidas, que son la región a la izquierda del punto A, la región comprendida entre los puntos C y D, y la región a la derecha del punto G:
y dos regiones permitidas, que son la región comprendida entre los puntos A y C, y la región comprendida entre los puntos D y G:
Nótese que, al ser las dos regiones permitidas no conexas entre sí (están separadas por una región prohibida o barrera de potencial), el movimiento de la partícula transcurrirá de facto sólo en una de las dos regiones permitidas. Pero ¿en cuál de las dos? Pues en aquella región en la que se halle la partícula inicialmente. En el presente caso, la posición inicial de la partícula corresponde al punto G. Por tanto, la partícula se moverá siempre confinada en la región comprendida entre los puntos D y G, ya que la barrera de potencial a la izquierda de D convierte a la otra región permitida en inaccesible de facto.
Posiciones de equilibrio
En el movimiento unidimensional conservativo de una partícula, las posiciones de equilibrio se corresponden con los extremos locales de la función energía potencial (máximos equilibrio inestable; mínimos equilibrio estable). En el caso que nos ocupa, observamos que la curva tiene dos mínimos (en B y en F) y un máximo (en O). Hay, por tanto, tres posiciones de equilibrio (B, O y F).
Sin embargo, la pregunta exacta que se nos formula en este ejercicio es: ¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento?
Pues bien, la respuesta correcta es UNA (en concreto, F). Porque, teniendo el nivel de energía mecánica representado en la gráfica, resulta imposible para la partícula pasar por los puntos O (por quedar dentro de una región prohibida) y B (por quedar dentro de una región permitida pero inaccesible "de facto").








