Diferencia entre las páginas «Masa y centro de masas (CMR)» y «Colisiones de dos partículas»
Secciones
| Línea 1: | Línea 1: | ||
== | ==Definición== | ||
Una ''colisión'' entre dos partículas es una interacción entre dos partículas que ocurre en un espacio limitado y un intervalo de tiempo corto. | |||
[[Imagen:raquetbol.gif|right]] | |||
Un ejemplo típico es el choque de dos bolas de billar. Durante el breve periodo de colisión, cada partícula se contrae elásticamente una pequeña cantidad, para acto seguido volver a expandirse, saliendo cada bola despedida en la misma dirección o en una dirección diferente. Otro ejemplo similar es el choque de una pelota de tenis contra una raqueta o una superficie rígida. En la imagen vemos una imagen a cámara lenta del choque de una pelota de raquetbol chocando contra una pared (fuente: [http://courses.ncssm.edu/hsi/ HSI at NCSSM]). Vemos que durante el tiempo de colisión la pelota se deforma enormemente. | |||
Al considerar una colisión no nos interesa tanto el qué ocurre ''durante'' la colisión, sino la relación entre el estado de las partículas ''antes'' y ''después'' de la colisión. Para ello, lo que se utiliza es que las interacciones conservarán la [[Cantidad_de_movimiento_de_un_sistema_de_partículas|cantidad de movimiento]], el [[Momento_cinético_de_un_sistema_de_partículas|momento cinético]] y, en ciertas ocasiones, la [[Energía_cinética_de_un_sistema_de_partículas|energía cinética]]. | |||
También es una colisión un ''[[péndulo balístico]]'' en el cual una bala se empotra en un objeto masivo, comunicándole una cierta velocidad. Aunque la interacción de la bala y el péndulo se puede considerar que continúa tras la colisión (pues ahora forman el mismo sólido), los cambios bruscos de velocidad se producen en un intervalo reducido de tiempo. | |||
No es una colisión una interacción a grandes distancias o que se prolonga durante un periodo largo de tiempo. Por ejemplo, la atracción gravitatoria entre dos masas que orbitan la una alrededor de la otra es un estado permanente y no puede ser considerada una colisión. | |||
El concepto de intervalo de tiempo corto o largo es relativo. La comparación se hace con el intervalo de tiempo en el que estamos considerando el movimiento de la partículas. Por ejemplo, cuando se lanza un satélite a Saturno, la nave se mueve por la atracción gravitatoria solar durante años, por lo que esta atracción no es una colisión. Sin embargo, durante el camino, para acelerar la nave, se puede emplear el método de catapulta gravitatoria, haciéndola pasar junto a Júpiter y ganando energía en el encuentro. Este acercamiento a Júpiter dura algunos días y sí puede ser tratado como una colisión (aunque la nave no llega a “tocar” Júpiter, sólo su campo gravitatorio). | |||
==Choques unidimensionales== | |||
La descripción de una colisión suele hacerse en dos sistemas de referencia diferentes, ambos inerciales. Uno es el llamado ''sistema laboratorio'', que representa a un observador externo al sistema de dos partículas. El otro es el ''sistema centro de masas'' (CM), ligado al [[Centro_de_masas_de_un_sistema_de_part%C3%ADculas|centro de masas]] del sistema de dos partículas. En el sistema CM la descipción es más sencilla, pero, dado que las medidas experimentales son realizadas en el sistema laboratorio, el procedimiento habitual es comenzar el estudio en el sistema laboratorio, pasar al sistema centro de masas, analizar la colisión en éste, y luego transformar los resultados de vuelta al sistema laboratorio. | |||
Aquí, por simplicidad, consideraremos solo el choque de dos masas que, tras la colisión, se separan en la misma dirección en la que se acercaron. Esto permite usar cantidades escalares en lugar de vectores. | |||
< | Suponemos entonces dos partículas, de masas <math>m_1</math> y <math>m_2</math> que se mueven con velocidades iniciales <math>v_{1i}</math> y <math>v_{2i}</math>, respectivamente. Tras la colisión las velocidades pasarán a ser <math>v_{1f}</math> y <math>v_{2f}</math> | ||
Al ser un problema sencillo, puede prescindirse del sistema CM para determinar el resultado de la colisión. | |||
==Conservación de la cantidad de movimiento== | |||
Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y | |||
<center><math>m_1v_{1i}+m_2v_{2i} = m_1v_{1f} + m_2v_{2f}\,</math></center> | |||
Esta es la ecuación básica que gobierna las colisiones. | |||
De que se conserve la cantidad de movimiento se deduce que la velocidad del centro de masas permanece constante | |||
<center><math>v_C=\frac{m_1v_1+m_2v_2}{m_1+m_2}=\mathrm{cte}</math></center> | |||
Podemos medir las velocidades de cada partícula respecto al CM y obtener las velocidades relativas | |||
<center><math>v'_1 = v_1 - v_C = v_1 - \frac{m_1v_1+m_2v_2}{m_1+m_2} = \frac{m_2(v_1-v_2)}{m_1+m_2}</math>{{qquad}}{{qquad}}<math>v'_2 = \frac{m_1(v_2-v_1)}{m_1+m_2}</math></center> | |||
Estas velocidades relativas verifican la condición | |||
<center><math>m_1v'_1+m_2v'_2 = 0\,</math></center> | |||
<center><math> | |||
tanto antes como después de la colisión. | |||
==Conservación de la energía== | |||
La energía cinética no se conserva en general en una colisión, sino que suele disiparse parcialmente. Una pelota que rebota en el suelo no vuelve a alcanzar la altura desde la que partió. | |||
Esto quiere decir que habrá una diferencia en la energía cinética debido a la colisión | |||
=== | <center><math>Q = \Delta K = K_f-K_i = \left(\frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2\right) - \left(\frac{1}{2}m_1v_{1i}^2 + \frac{1}{2}m_2v_{2i}^2\right)</math></center> | ||
Esta energía o bien se manifiesta como un aumento de la temperatura de las partículas, o bien se pierde en forma de calor (o un poco de cada cosa). | |||
de | Dependiendo de la cantidad de energía cinética que se pierda, puede hacerse una clasificación de las colisiones: | ||
;Colisión perfectamente elástica: Es aquella en la que no se disipa energía cinética y ésta se conserva. | |||
;Colisión inelástica: Aquella en la que se disipa parte de la energía cinética. | |||
;Colisión completamente inelástica: Aquella en la que se disipa el máximo de energía. Este máximo no es ''toda'' la energía cinética en el sistema laboratorio, ya que la conservación de la cantidad de movimiento impone que el sistema se mueva tras la colisión, y por tanto conserve parte de la energía cinética. | |||
:Las colisiones completamente inelásticas se dan cuando los dos partículas se fusionan y continúan su marcha como una sola partícula con masa la suma de las dos originales. | |||
o, | ;Explosiones: Un proceso que no es estrictamente una colisión, pero que puede ser tratado matemáticamente como una, es el de la explosión. Una sola partícula se descompone en dos (o más) fragmentos, que pasan a moverse por separado. Vendría a ser el opuesto de una colisión completamente inelástica. En este caso la energía cinética del sistema ''aumenta'', normalmente a costa de la energía interna de origen químico. | ||
===Coeficiente de restitución=== | |||
Para caracterizar el tipo de colisión del que se trata se define un parámetro denominado ''coeficiente de restitución'' | |||
<center><math> | <center><math>C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}}</math></center> | ||
que en términos geométricos representa la proporción entre la velocidad relativa con la que se alejan las partícula y la velocidad con la que se acercaban. El coeficiente de restitución tiene l mismo valor en el sistema laboratorio que en el sistema centro de masas. | |||
En una colisión perfectamente elástica, <math>C_R=1</math> y las partículas se alejan con la misma velocidad con la que se acercaban. | |||
En una colisión completamente inelástica, <math>C_R=0</math> y las partículas no se alejan tras la colisión. | |||
Para un caso intermedio se tendrá que <math>0 < C_R < 1</math>. | |||
==Colisión perfectamente elástica== | |||
Vamos a determinar las velocidades finales en el caso de que se conserve la energía cinética. Para ello debemos resolver el sistema de dos ecuaciones con dos incógnitas | |||
<center><math>\begin{array}{ccccccc}m_1v_{1i}&+&m_2v_{2i}&= & m_1v_{1f}&+& m_2v_{2f} \\ | |||
&& \\ | |||
\displaystyle \frac{1}{2}m_1v_{1i}^2&+&\displaystyle\frac{1}{2}m_2v_{2i}^2 & = & \displaystyle \frac{1}{2}m_1v_{1f}^2&+&\displaystyle\frac{1}{2}m_2v_{2f}^2 | |||
\end{array}</math></center> | |||
que podemos reescribir, reagrupando términos y factorizando | |||
<center><math>\ | <center><math>\begin{array}{rcl}m_1(v_{1i}-v_{1f})&= & m_2(v_{2f}-v_{2i}) \\ | ||
&& \\ | |||
\displaystyle \frac{1}{2}m_1(v_{1i}-v_{1f})(v_{1i}+v_{1f}) & = & \displaystyle \frac{1}{2}m_2(v_{2f}-v_{2i})(v_{2f}+v_{2i}) | |||
\end{array}</math></center> | |||
Sustituyendo la primera en la segunda llegamos a que efectivamente el coeficiente de restitución es igual a la unidad. | |||
<center><math>\ | <center><math> | ||
v_{1i}+v_{1f}=v_{2i}+v_{2f}\,</math>{{tose}}<math>v_{2f}-v_{1f}=-(v_{2i}-v_{1i})\,</math>{{tose}}<math>C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}} = 1</math></center> | |||
Combinando esta relación la ley de conservación de la cantidad de movimiento tenemos un sistema de dos ecuaciones lienales con dos incógnitas, con solución | |||
<center><math> | <center><math>v_{1f} = \frac{m_1-m_2}{m_1+m_2}v_{1i} + \frac{2m_2}{m_1+m_2}v_{2i}</math>{{qquad}}{{qquad}}<math>v_{2f} = \frac{2m_1}{m_1+m_2}v_{1i}+\frac{m_2-m_1}{m_1+m_2}v_{2i}</math></center> | ||
===Choque de dos masas iguales=== | |||
[[Imagen:newtoncradle.gif|right|thumb|Cuna de Newton]] | |||
[[ | |||
Un caso particular importante es aquel en que las dos partículas que colisionan tienen la misma masa. En este caso | |||
{{ | <center><math>v_{1f}= v_{2i}\,</math>{{qquad}}{{qquad}}<math>v_{2f}=v_{1i}\,</math></center> | ||
En | Las dos partículas intercambian sus velocidades. En particular si se trata de una partícula que choca contra una que está en reposo, la primera se queda “clavada”, mientras que la segunda sale con la velocidad que llevaba la primera. Este es un fenómeno común en el billar y la base del dispositivo conocido como ''cuna de Newton'', en el que varias bolas colisionan sucesivamente. | ||
===Caso de un blanco en reposo=== | |||
Un caso importante entre las colisiones es el representado por una partícula móvil (''proyectil'') que impacta sobre una fija (''blanco''). | |||
Matemáticamente la condición es | |||
<center><math> | <center><math>v_{1i}=v_0\qquad v_{2i}=0</math></center> | ||
lo que nos da las velocidades resultantes | |||
== | <center><math>v_{1f} = \frac{m_1-m_2}{m_1+m_2}v_{0}</math>{{qquad}}{{qquad}}<math>v_{2f} = \frac{2m_1}{m_1+m_2}v_{0}</math></center> | ||
Los resultados dependen de la proporción entre las masas. Si <math>\gamma = m_1/m_2</math> queda | |||
<center><math>\gamma=\frac{m_1}{m_2}</math>{{tose}}<math>v_{1f}=\frac{\gamma-1}{1+\gamma}v_0</math>{{qquad}}{{qquad}}<math>v_{2f}=\frac{2\gamma}{1+\gamma}v_0</math></center> | |||
=== | ====Blanco masivo==== | ||
Cuando el blanco es más pesado que el proyectil (<math>m_2>m_1</math>, o <math>\gamma<1</math>), <math>v_{1f}</math> se hace negativo, lo cual quiere decir que el proyectil rebota. | |||
El caso límite es aquel en que el blanco es infinitamente masivo. Esto corresponde, por ejemplo, al choque de una pelota contra una pared. En este caso | |||
<center><math>\gamma\to0\qquad\Rightarrow\qquad v_{1f}\to -v_0\qquad\qquad v_{2f}\to 0</math></center> | |||
esto es, el proyectil rebota con la misma velocidad con la que venía. El blanco permanece inmóvil (aunque adquiere la cantidad de movimiento que pierde el proyectil). | |||
====Blanco ligero==== | |||
En el otro extremo tenemos el caso del blanco más ligero que el proyectil (“matar moscas a cañonazos”). En esta caso <math>\gamma > 1</math> y <math>v_{1f}>0</math>, lo que quiere decir que el proyectil no rebota, sino que continúa hacia adelante, con una velocidad menor que la incidente. El blanco sale despedido con una velocidad mayor que la del proyectil, por lo que se separa de éste. | |||
[[ | En el caso límite de proyectil infinitamente masivo (<math>\gamma\to \infty</math>) el proyectil continúa su camino imperturbado, mientras que el blanco sale disparado con una velocidad doble de la del proyectil | ||
<center><math>\gamma\to \infty\qquad\Rightarrow\qquad v_{1f}\to v_0\qquad\qquad v_{2f}\to 2v_0</math></center> | |||
Podemos representar los resultados para los dos casos en una gráfica semilogarítmica. A la izquierda tenemos el límite de blanco ligero y a la derecha el de blanco infinitamente pesado. En la posición central tenemos el caso de dos masas iguales. | |||
<center>[[Imagen:v1v2colision.png]]</center> | |||
Obtenemos una gráfica diferente si en lugar de representar las velocidades representamos la cantidad de movimiento de cada partícula, comparada con la inicial del proyectil. En este caso tenemos | |||
<center><math>p_0=m_1v_0\qquad\qquad p_{1f}=m_1v_{1f}=\frac{\gamma -1}{\gamma+1}p_0</math>{{qquad}}{{qquad}}<math>p_{2f}=m_2v_{2f}=\frac{2}{\gamma+1}p_0</math></center> | |||
<center>[[Imagen:p1p2colision.png]]</center> | |||
Vemos que, cuando el proyectil es muy ligero comparado con el blanco, éste se lleva el doble de cantidad de movimiento que traía inicilamente el proyectil, pese a que la velocidad del blanco es prácticamente nula (este es es el caso de una pelota que choca con una pared; aunque ésta casi no se mueve, sí se lleva cantidad de movimiento). | |||
También podemos representar la energía cinética de cada partícula, comparada con la inicial. | |||
<center><math>K_0=\frac{1}{2}m_1v_0^2\qquad\qquad K_{1f}=\frac{1}{2}m_1v_{1f}=\left(\frac{\gamma -1}{\gamma+1}\right)^2K_0</math>{{qquad}}{{qquad}}<math>K_{2f}=\frac{1}{2}m_2v_{2f}^2=\frac{4\gamma}{(\gamma+1)^2}K_{0}</math></center> | |||
<center>[[Imagen:K1K2colision.gif]]</center> | |||
Vemos que, tanto si el proyectil es muy ligero como si es muy pesado la energía con la que sale de la colisión es casi igual a la de entrada, y que el máximo de transferencia de energía al blanco se da cuando las dos masas son iguales (en cuyo caso le cede toda la energía. | |||
==Colisión completamente inelástica== | |||
En el otro extremo en cuanto a la energía cinética se encuentra la colisión completamente inelástica, en la que se disipa el máximo de energía. | |||
Podemos calcular el máximo de energía disipada, [[Energía_cinética_de_un_sistema_de_partículas#Descomposici.C3.B3n_de_la_energ.C3.ADa_cin.C3.A9tica|descomponiendo la energía cinética]] en suma de energía cinética del CM, más energía cinética relativa | |||
<center><math>K = K_C + K' = \frac{m_1+m_2}{2}v_C^2 + \left(\frac{1}{2}m_1{v'_1}^2+\frac{1}{2}m_2{v'_2}^2\right)</math></center> | |||
El primer término es constante, por serlo la velocidad del CM. Por ello, el máximo de la energía disipada se dará cuando las velocidades relativas al CM, tras la colisión sean nulas, esto es, cuando las dos partículas resulten con la misma velocidad, que será la del CM, | |||
<center><math>v'_{1f}=0\qquad v'_{2f}=0</math>{{tose}}<math>K'_f = 0\qquad \Delta K = K_C - K_i\,</math></center> | |||
La velocidad del CM, que será la de la única partícula resultante es | |||
<center><math>v_{1f}=v_{2f}=v_C=\frac{m_1v_{1i}+m_2v_{2i}}{m_1+m_2}</math></center> | |||
En el caso particular de un proyectil que impacta con un blanco, esta velocidad se reduce a | |||
<center><math>v_{1i}=v_0\qquad v_{2i}=0\qquad\Rightarrow\qquad v_{1f}=v_{2f}=v_C=\frac{m_1}{m_1+m_2}v_0=\frac{\gamma v_0}{1+\gamma}</math></center> | |||
Si el proyectil es muy ligero comparado con el blanco esta velocidad se aproxima a <math>\gamma v_0</math>. Esto es lo que ocurre en un [[péndulo balístico]]; si es mucho más pesado, el proyectil se lleva al blanco por delante y continúa su marcha casi inalterado (como un tren que choca con una mosca estacionaria). | |||
Podemos representar la energía final comparada con la inicial, así como la pérdida relativa de energía | |||
<center><math>K_0=\frac{1}{2}m_1v_0^2\qquad\qquad K_f = \frac{1}{2}(m_1+m_2)v_C^2=\frac{\gamma}{1+\gamma}K_0\qquad\qquad K_0-K_f = -\Delta K=\frac{1}{1+\gamma}K_0</math></center> | |||
<center>[[Imagen:K0Kfinelastica.gif]]</center> | |||
Si el proyectil es muy ligero se pierde casi toda la energía, pero si es muy pesado comparado con el blanco, la energía apenas se disipa. | |||
==Colisiones en tres dimensiones== | |||
El problema general de una colisión de dos partículas en tres dimensiones, cuando la dirección en que se desvían la partículas no coincide con la dirección de movimiento inicial es bastante más complicado y ofrece una gran variedad de casos posibles. | |||
Aquí sólo consideraremos el más simple: el choque perfectamente elástico de dos partículas de la misma masa, cuando una de ellas (el proyectil) impacta sobre la otra (el blanco) que se encuentra estacionaria. Esta es, aproximadamente, la situación que se produce en el billar cuando el impacto no es frontal. | |||
Supondremos un sistema de referencia con origen en en el blanco y con eje X el de incidencia del proyectil, de forma que las velocidades iniciales son | |||
<center><math>m_1=m_2=m\qquad\qquad \mathbf{v}_{1i}=v_0\mathbf{i}\qquad\qquad \mathbf{v}_{2i}=\mathbf{0}</math></center> | |||
[[Imagen:colision-plano.gif|right]] | |||
Tras la colisión, la partícula 1 se desvía en un ángulo <math>\theta</math>, mientras que la 2 lo hace un ángulo <math>\varphi</math> hacia el otro lado, por lo que las velocidades finales son | |||
<center><math>\mathbf{v}_{1f}=v_{1f}\cos\theta\mathbf{i}+v_{1f}\,\mathrm{sen}\,\theta\,\mathbf{j}</math>{{qquad}}{{qquad}}<math>\mathbf{v}_{2f}=v_{2f}\cos\varphi\mathbf{i}-v_{2f}\,\mathrm{sen}\,\varphi\,\mathbf{j}</math></center> | |||
[[Imagen:choque-esferas.gif|left]] | |||
Cuando se trata de partículas puntuales, el ángulo <math>\theta</math> queda indeterminado y hay que darlo como un dato adicional del problema. Para sólidos reales, como esferas, el ángulo <math>\theta</math> lo determina el que las esferas no incidan centralmente, sino a una cierta distancia del centro (denominada habitualmente ''parámetro de impacto'', <math>b</math>). | |||
La conservación de la cantidad de movimiento impone que | |||
<center><math>m\mathbf{v}_{1i}+m\mathbf{v}_{2i}=m\mathbf{v}_{1f}+m\mathbf{v}_{2f}\,</math></center> | |||
Dividiendo por la masa y sustituyendo las velocidades iniciales | |||
<center><math>\mathbf{v}_0=\mathbf{v}_{1f}+\mathbf{v}_{2f}</math></center> | |||
La conservación de la energía implica | |||
Al ser la colisión elástica, también se conserva la energía cinética, por lo que | |||
<center><math>\frac{1}{2}mv_0^2 = \frac{1}{2}mv_{1f}^2+\frac{1}{2}mv_{2f}^2</math></center> | |||
Multiplicando por <math>2/m</math> | |||
<center><math>v_0^2 = v_{1f}^2+v_{2f}^2</math></center> | |||
Si multiplicamos escalarmente la conservación del momento por sí misma | |||
<center><math>v^2_0=(\mathbf{v}_{1f}+\mathbf{v}_{2f})\cdot(\mathbf{v}_{1f}+\mathbf{v}_{2f})=v^2_{1f}+v^2_{2f}+2\mathbf{v}_{1f}\cdot\mathbf{v}_{2f}</math></center> | |||
Restando la ley de conservación de la energía llegamos a la condición | |||
<center><math>\mathbf{v}_{1f}\cdot\mathbf{v}_{2f}=0</math></center> | |||
que implica que las partículas se separan siguiendo trayectorias ortogonales (o bien una de las dos partículas se queda inmóvil tras la colisión). En términos de los ángulos | |||
<center><math>\theta+\varphi=\frac{\pi}{2}</math></center> | |||
En cuanto a la celeridad con la que se aleja cada una, depende del ángulo de desviación. Por la ortogonalidad tenemos | |||
<center><math>\mathbf{v}_{1f}=v_{1f}(\cos\theta\mathbf{i}+\,\mathrm{sen}\,\theta\,\mathbf{j})</math>{{qquad}}{{qquad}}<math>\mathbf{v}_{2f}=v_{2f}(\mathrm{sen}\,\theta\,\mathbf{i}-\cos\theta\,\mathbf{j})</math></center> | |||
Sustituyendo en la conservación de la cantidad de movimiento e igualando componente a componente quedan las ecuaciones | |||
<center><math>v_0 = v_{1f}\cos\theta+v_{2f}\,\mathrm{sen}\,\theta</math>{{qquad}}{{qquad}}<math>0 = v_{1f}\,\mathrm{sen}\,\theta-v_{2f}\cos\theta</math></center> | |||
de donde | |||
<center><math>v_{1f}=v_0\cos\theta\,</math>{{qquad}}{{qquad}}<math>v_{2f}=v_0\,\mathrm{sen}\,\theta</math></center> | |||
siendo las energías cinéticas resultantes | |||
<center><math>K_{1f}=K_0\cos^2\theta\qquad\qquad K_{2f}=K_0\,\mathrm{sen}^2\theta</math></center> | |||
Para un ángulo de desviación <math>\theta= 0</math>, el proyectil se lleva toda la energía y el blanco se queda parado. realmente en este caso no hay colisión. | |||
Si el ángulo de desviación es el máximo posible <math>\theta=\pi/2</math>, el proyectil se queda parado y el blanco se aleja en la misma dirección. Este es de nuevo el caso unidimensional que ya conocemos. | |||
Para <math>\pi/4</math> las dos partículas se reparten la energía a partes iguales y se marchan en direcciones simétricas respecto a la línea de incidencia. | |||
[[Categoría:Dinámica de un sistema de partículas]] | |||
[[Categoría:Problemas de dinámica de un sistema de partículas]] | |||
Revisión del 14:25 16 nov 2023
Definición
Una colisión entre dos partículas es una interacción entre dos partículas que ocurre en un espacio limitado y un intervalo de tiempo corto.

Un ejemplo típico es el choque de dos bolas de billar. Durante el breve periodo de colisión, cada partícula se contrae elásticamente una pequeña cantidad, para acto seguido volver a expandirse, saliendo cada bola despedida en la misma dirección o en una dirección diferente. Otro ejemplo similar es el choque de una pelota de tenis contra una raqueta o una superficie rígida. En la imagen vemos una imagen a cámara lenta del choque de una pelota de raquetbol chocando contra una pared (fuente: HSI at NCSSM). Vemos que durante el tiempo de colisión la pelota se deforma enormemente.
Al considerar una colisión no nos interesa tanto el qué ocurre durante la colisión, sino la relación entre el estado de las partículas antes y después de la colisión. Para ello, lo que se utiliza es que las interacciones conservarán la cantidad de movimiento, el momento cinético y, en ciertas ocasiones, la energía cinética.
También es una colisión un péndulo balístico en el cual una bala se empotra en un objeto masivo, comunicándole una cierta velocidad. Aunque la interacción de la bala y el péndulo se puede considerar que continúa tras la colisión (pues ahora forman el mismo sólido), los cambios bruscos de velocidad se producen en un intervalo reducido de tiempo.
No es una colisión una interacción a grandes distancias o que se prolonga durante un periodo largo de tiempo. Por ejemplo, la atracción gravitatoria entre dos masas que orbitan la una alrededor de la otra es un estado permanente y no puede ser considerada una colisión.
El concepto de intervalo de tiempo corto o largo es relativo. La comparación se hace con el intervalo de tiempo en el que estamos considerando el movimiento de la partículas. Por ejemplo, cuando se lanza un satélite a Saturno, la nave se mueve por la atracción gravitatoria solar durante años, por lo que esta atracción no es una colisión. Sin embargo, durante el camino, para acelerar la nave, se puede emplear el método de catapulta gravitatoria, haciéndola pasar junto a Júpiter y ganando energía en el encuentro. Este acercamiento a Júpiter dura algunos días y sí puede ser tratado como una colisión (aunque la nave no llega a “tocar” Júpiter, sólo su campo gravitatorio).
Choques unidimensionales
La descripción de una colisión suele hacerse en dos sistemas de referencia diferentes, ambos inerciales. Uno es el llamado sistema laboratorio, que representa a un observador externo al sistema de dos partículas. El otro es el sistema centro de masas (CM), ligado al centro de masas del sistema de dos partículas. En el sistema CM la descipción es más sencilla, pero, dado que las medidas experimentales son realizadas en el sistema laboratorio, el procedimiento habitual es comenzar el estudio en el sistema laboratorio, pasar al sistema centro de masas, analizar la colisión en éste, y luego transformar los resultados de vuelta al sistema laboratorio.
Aquí, por simplicidad, consideraremos solo el choque de dos masas que, tras la colisión, se separan en la misma dirección en la que se acercaron. Esto permite usar cantidades escalares en lugar de vectores.
Suponemos entonces dos partículas, de masas y que se mueven con velocidades iniciales y , respectivamente. Tras la colisión las velocidades pasarán a ser y
Al ser un problema sencillo, puede prescindirse del sistema CM para determinar el resultado de la colisión.
Conservación de la cantidad de movimiento
Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y
Esta es la ecuación básica que gobierna las colisiones.
De que se conserve la cantidad de movimiento se deduce que la velocidad del centro de masas permanece constante
Podemos medir las velocidades de cada partícula respecto al CM y obtener las velocidades relativas
Estas velocidades relativas verifican la condición
tanto antes como después de la colisión.
Conservación de la energía
La energía cinética no se conserva en general en una colisión, sino que suele disiparse parcialmente. Una pelota que rebota en el suelo no vuelve a alcanzar la altura desde la que partió.
Esto quiere decir que habrá una diferencia en la energía cinética debido a la colisión
Esta energía o bien se manifiesta como un aumento de la temperatura de las partículas, o bien se pierde en forma de calor (o un poco de cada cosa).
Dependiendo de la cantidad de energía cinética que se pierda, puede hacerse una clasificación de las colisiones:
- Colisión perfectamente elástica
- Es aquella en la que no se disipa energía cinética y ésta se conserva.
- Colisión inelástica
- Aquella en la que se disipa parte de la energía cinética.
- Colisión completamente inelástica
- Aquella en la que se disipa el máximo de energía. Este máximo no es toda la energía cinética en el sistema laboratorio, ya que la conservación de la cantidad de movimiento impone que el sistema se mueva tras la colisión, y por tanto conserve parte de la energía cinética.
- Las colisiones completamente inelásticas se dan cuando los dos partículas se fusionan y continúan su marcha como una sola partícula con masa la suma de las dos originales.
- Explosiones
- Un proceso que no es estrictamente una colisión, pero que puede ser tratado matemáticamente como una, es el de la explosión. Una sola partícula se descompone en dos (o más) fragmentos, que pasan a moverse por separado. Vendría a ser el opuesto de una colisión completamente inelástica. En este caso la energía cinética del sistema aumenta, normalmente a costa de la energía interna de origen químico.
Coeficiente de restitución
Para caracterizar el tipo de colisión del que se trata se define un parámetro denominado coeficiente de restitución
que en términos geométricos representa la proporción entre la velocidad relativa con la que se alejan las partícula y la velocidad con la que se acercaban. El coeficiente de restitución tiene l mismo valor en el sistema laboratorio que en el sistema centro de masas.
En una colisión perfectamente elástica, y las partículas se alejan con la misma velocidad con la que se acercaban.
En una colisión completamente inelástica, y las partículas no se alejan tras la colisión.
Para un caso intermedio se tendrá que .
Colisión perfectamente elástica
Vamos a determinar las velocidades finales en el caso de que se conserve la energía cinética. Para ello debemos resolver el sistema de dos ecuaciones con dos incógnitas
que podemos reescribir, reagrupando términos y factorizando
Sustituyendo la primera en la segunda llegamos a que efectivamente el coeficiente de restitución es igual a la unidad.
Combinando esta relación la ley de conservación de la cantidad de movimiento tenemos un sistema de dos ecuaciones lienales con dos incógnitas, con solución
Choque de dos masas iguales

Un caso particular importante es aquel en que las dos partículas que colisionan tienen la misma masa. En este caso
Las dos partículas intercambian sus velocidades. En particular si se trata de una partícula que choca contra una que está en reposo, la primera se queda “clavada”, mientras que la segunda sale con la velocidad que llevaba la primera. Este es un fenómeno común en el billar y la base del dispositivo conocido como cuna de Newton, en el que varias bolas colisionan sucesivamente.
Caso de un blanco en reposo
Un caso importante entre las colisiones es el representado por una partícula móvil (proyectil) que impacta sobre una fija (blanco).
Matemáticamente la condición es
lo que nos da las velocidades resultantes
Los resultados dependen de la proporción entre las masas. Si queda
Blanco masivo
Cuando el blanco es más pesado que el proyectil (, o ), se hace negativo, lo cual quiere decir que el proyectil rebota.
El caso límite es aquel en que el blanco es infinitamente masivo. Esto corresponde, por ejemplo, al choque de una pelota contra una pared. En este caso
esto es, el proyectil rebota con la misma velocidad con la que venía. El blanco permanece inmóvil (aunque adquiere la cantidad de movimiento que pierde el proyectil).
Blanco ligero
En el otro extremo tenemos el caso del blanco más ligero que el proyectil (“matar moscas a cañonazos”). En esta caso y , lo que quiere decir que el proyectil no rebota, sino que continúa hacia adelante, con una velocidad menor que la incidente. El blanco sale despedido con una velocidad mayor que la del proyectil, por lo que se separa de éste.
En el caso límite de proyectil infinitamente masivo () el proyectil continúa su camino imperturbado, mientras que el blanco sale disparado con una velocidad doble de la del proyectil
Podemos representar los resultados para los dos casos en una gráfica semilogarítmica. A la izquierda tenemos el límite de blanco ligero y a la derecha el de blanco infinitamente pesado. En la posición central tenemos el caso de dos masas iguales.

Obtenemos una gráfica diferente si en lugar de representar las velocidades representamos la cantidad de movimiento de cada partícula, comparada con la inicial del proyectil. En este caso tenemos

Vemos que, cuando el proyectil es muy ligero comparado con el blanco, éste se lleva el doble de cantidad de movimiento que traía inicilamente el proyectil, pese a que la velocidad del blanco es prácticamente nula (este es es el caso de una pelota que choca con una pared; aunque ésta casi no se mueve, sí se lleva cantidad de movimiento).
También podemos representar la energía cinética de cada partícula, comparada con la inicial.
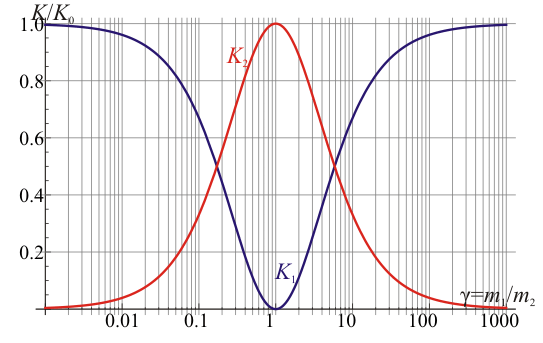
Vemos que, tanto si el proyectil es muy ligero como si es muy pesado la energía con la que sale de la colisión es casi igual a la de entrada, y que el máximo de transferencia de energía al blanco se da cuando las dos masas son iguales (en cuyo caso le cede toda la energía.
Colisión completamente inelástica
En el otro extremo en cuanto a la energía cinética se encuentra la colisión completamente inelástica, en la que se disipa el máximo de energía.
Podemos calcular el máximo de energía disipada, descomponiendo la energía cinética en suma de energía cinética del CM, más energía cinética relativa
El primer término es constante, por serlo la velocidad del CM. Por ello, el máximo de la energía disipada se dará cuando las velocidades relativas al CM, tras la colisión sean nulas, esto es, cuando las dos partículas resulten con la misma velocidad, que será la del CM,
La velocidad del CM, que será la de la única partícula resultante es
En el caso particular de un proyectil que impacta con un blanco, esta velocidad se reduce a
Si el proyectil es muy ligero comparado con el blanco esta velocidad se aproxima a . Esto es lo que ocurre en un péndulo balístico; si es mucho más pesado, el proyectil se lleva al blanco por delante y continúa su marcha casi inalterado (como un tren que choca con una mosca estacionaria).
Podemos representar la energía final comparada con la inicial, así como la pérdida relativa de energía
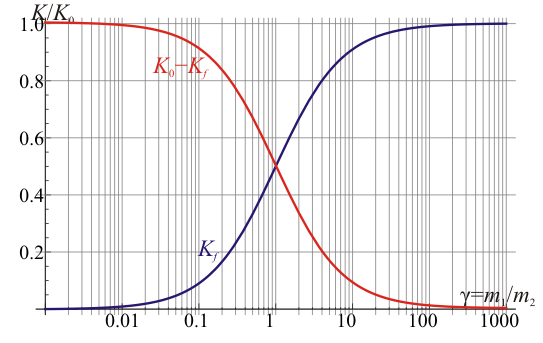
Si el proyectil es muy ligero se pierde casi toda la energía, pero si es muy pesado comparado con el blanco, la energía apenas se disipa.
Colisiones en tres dimensiones
El problema general de una colisión de dos partículas en tres dimensiones, cuando la dirección en que se desvían la partículas no coincide con la dirección de movimiento inicial es bastante más complicado y ofrece una gran variedad de casos posibles.
Aquí sólo consideraremos el más simple: el choque perfectamente elástico de dos partículas de la misma masa, cuando una de ellas (el proyectil) impacta sobre la otra (el blanco) que se encuentra estacionaria. Esta es, aproximadamente, la situación que se produce en el billar cuando el impacto no es frontal.
Supondremos un sistema de referencia con origen en en el blanco y con eje X el de incidencia del proyectil, de forma que las velocidades iniciales son
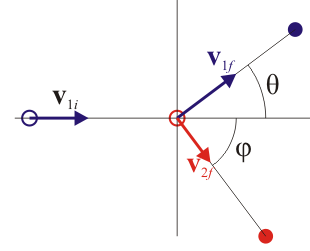
Tras la colisión, la partícula 1 se desvía en un ángulo , mientras que la 2 lo hace un ángulo hacia el otro lado, por lo que las velocidades finales son
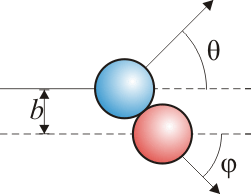
Cuando se trata de partículas puntuales, el ángulo queda indeterminado y hay que darlo como un dato adicional del problema. Para sólidos reales, como esferas, el ángulo lo determina el que las esferas no incidan centralmente, sino a una cierta distancia del centro (denominada habitualmente parámetro de impacto, ).
La conservación de la cantidad de movimiento impone que
Dividiendo por la masa y sustituyendo las velocidades iniciales
La conservación de la energía implica
Al ser la colisión elástica, también se conserva la energía cinética, por lo que
Multiplicando por
Si multiplicamos escalarmente la conservación del momento por sí misma
Restando la ley de conservación de la energía llegamos a la condición
que implica que las partículas se separan siguiendo trayectorias ortogonales (o bien una de las dos partículas se queda inmóvil tras la colisión). En términos de los ángulos
En cuanto a la celeridad con la que se aleja cada una, depende del ángulo de desviación. Por la ortogonalidad tenemos
Sustituyendo en la conservación de la cantidad de movimiento e igualando componente a componente quedan las ecuaciones
de donde
siendo las energías cinéticas resultantes
Para un ángulo de desviación , el proyectil se lleva toda la energía y el blanco se queda parado. realmente en este caso no hay colisión.
Si el ángulo de desviación es el máximo posible , el proyectil se queda parado y el blanco se aleja en la misma dirección. Este es de nuevo el caso unidimensional que ya conocemos.
Para las dos partículas se reparten la energía a partes iguales y se marchan en direcciones simétricas respecto a la línea de incidencia.









































































