|
|
| Línea 1: |
Línea 1: |
| == Enunciado ==
| | = Enunciado = |
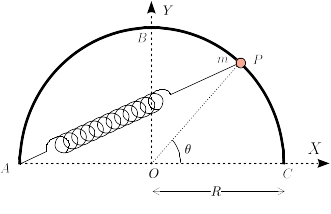
| Una partícula de masa <math>m</math> se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme <math>\omega</math> en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como | | [[File:F1GIERM-particula-aro-muelle-cinetico-enunciado.png|right]] |
| <center><math>
| | Una partícula de masa <math>m</math> está engarzada en un semiaro de radio <math>R</math>. Un muelle de |
| \begin{matrix}
| | constante elástica <math>k=mg/R</math> y longitud natural nula conecta la partícula y el punto <math>A</math> |
| x(t) = r(t)\,\cos(\omega t)&\qquad\qquad& y(t) = r(t)\,\,\mathrm{sen}\,(\omega t)
| | del semiaro. La gravedad no actúa. |
| \end{matrix}
| | #Dibuja el diagrama de fuerzas de la partícula. |
| </math></center>
| | #Escribe la expresión que da el momento cinético de la partícula respecto al punto <math>O</math>. |
| #Halla la ecuación diferencial que cumple la función <math>r(t)</math> sabiendo que el vínculo entre la partícula y el tubo es liso.
| | #Aplicando el Teorema del Momento Cinético, encuentra la ecuación de movimiento de la partícula. |
| #Comprueba que
| |
| <center><math>
| |
| r(t) = A\,e^{\omega t}
| |
| </math></center> | |
| es una solución de la ecuación para <math>r(t)</math>.
| |
| #Para esta solución particular | |
| ##Calcula la fuerza ejercida por el tubo en cada instante.
| |
| ##Halla la potencia desarrollada por el tubo sobre la partícula. Calcula el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de <math>r=b</math> a <math>r=2b</math>. | |
| ##Calcula el incremento de la energía cinética de la partícula en el mismo intervalo u comprueba que se verifica el teorema de las fuerzas vivas o de la energía. | |
|
| |
|
| == Solución ==
| | = Solución = |
|
| |
|
| === Ecuaciones de movimiento === | | == Diagrama de fuerzas == |
| | | [[File:F1GIERM-particula-aro-muelle-cinetico-fuerzas.png|right]] |
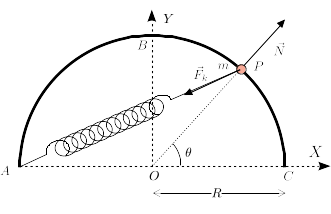
| [[Imagen:F1_GIA_tubo_rotando_fuerza.png|right]] | | La figura de la derecha muestra las fuerzas que actúan sobre la partícula. La fuerza vincular |
| | | <math>\vec{N}</math> es perpendicular al aro, es decir, radial. La fuerza del muelle apunta hacia |
| La ecuación de movimiento es la Segunda Ley de Newton | | el punto de anclaje del muelle <math>A</math>. Las expresiones de estas fuerzas son |
| <center>
| | <center><math> |
| <math>
| |
| m\,\vec{a} = \sum\limits_{i=1}^n\vec{F}_i + \sum\limits_{j=i}^s\vec{\Phi}_j
| |
| </math>
| |
| </center>
| |
| donde <math>\vec{F}_i </math> son las fuerzas activas y <math>\vec{\Phi}_j </math> son las fuerzas de reacción vincular
| |
| que actúan sobre las partículas. | |
| | |
| En este problema no hay fuerzas activas, pues no se habla del peso. La única fuerza que actúa sobre la partícula
| |
| es la fuerza de reacción vincular, <math>\vec{\Phi} </math>, que ejerce sobre ella el tubo cuando gira, obligándola a permanecer dentro de él.
| |
| El enunciado dice que el vínculo es liso. Esto quiere decir que <math>\vec{\Phi} </math> es perpendicular al tubo.
| |
| Por tanto la segunda Ley de Newton queda
| |
| <center>
| |
| <math> | |
| m\,\vec{a} = \vec{\Phi}
| |
| </math> | |
| </center>
| |
| | |
| | |
| Vamos a resolver el problema usando coordenadas polares. En estas coordenadas los vectores de posición, velocidad y
| |
| aceleración son
| |
| <center> | |
| <math> | |
| \begin{array}{l} | | \begin{array}{l} |
| \vec{r} = \rho\,\vec{u}_{\rho} \\ \\ | | \vec{N} = N\cos\theta\,\vec{\imath} + N\,\mathrm{sen}\,\theta\,\vec{\jmath},\\ |
| \vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta} \\ \\
| | \vec{F}_k = -k\overrightarrow{AP} = |
| \vec{a} = (\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta})\,\vec{u}_{\theta} | | -k(\overrightarrow{OP}-\overrightarrow{OA}) |
| | = -kR(1+\cos\theta)\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}. |
| \end{array} | | \end{array} |
| </math> | | </math></center> |
| </center>
| | Hemos usado los vectores |
| {{ac|Coordenadas polares}}
| | <center><math> |
| | |
| En este problema la partícula está obligada a permanecer dentro del tubo, y este gira con velocidad angular constante
| |
| <math>\omega </math>. Por tanto, la variación del ángulo <math> \theta </math> con el tiempo es
| |
| <center>
| |
| <math>
| |
| \theta(t) = \omega\,t
| |
| </math>
| |
| </center> | |
| Hemos tomado <math>\theta(0)=0 </math> para simplificar. Por tanto, en este caso las expresiones de la posición, la | |
| velocidad y la aceleración quedan
| |
| <center> | |
| <math> | |
| \begin{array}{l} | | \begin{array}{l} |
| \vec{r} = \rho\,\vec{u}_{\rho} \\ \\ | | \overrightarrow{OP} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath},\\ |
| \vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\omega\,\vec{u}_{\theta} \\ \\
| | \overrightarrow{OA} = - R\,\vec{\imath}. |
| \vec{a} = (\ddot{\rho}-\rho\,\omega^2)\,\vec{u}_{\rho} + 2\,\dot{\rho}\,\omega\,\vec{u}_{\theta} | |
| \end{array} | | \end{array} |
| </math> | | </math></center> |
| </center> | |
|
| |
|
| La expresión de la fuerza de reacción vincular en coordenadas polares, al ser perpendicular al tubo, es
| |
| <center>
| |
| <math>
| |
| \vec{\Phi} = \Phi\,\vec{u}_{\theta}
| |
| </math>
| |
| </center>
| |
|
| |
|
| La Segunda Ley de Newton, que es una ecuación vectorial, da lugar en este caso a dos ecuaciones escalares,
| | == Momento cinético == |
| una por cada componente
| | El momento cinético respecto del punto <math>O</math> es |
| <center> | | <center><math> |
| <math> | | \vec{L}_O = \overrightarrow{OP}\times(m\vec{v}). |
| m\vec{a} = \vec{\Phi} \rightarrow
| | </math></center> |
| \left\{
| | El vector velocidad es |
| \begin{array}{lcl} | | <center><math> |
| \vec{u}_{\rho} & \to & m(\ddot{\rho}-\rho\,\omega^2)=0 \\ & & \\ | | \vec{v}=\dot{\overrightarrow{OP}} = -R\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} + |
| \vec{u}_{\theta} & \to & 2\,m\,\dot{\rho}\,\omega = \Phi | | R\dot{\theta}\cos\theta\,\vec{\jmath}. |
| \end{array}
| | </math></center> |
| \right.
| | Haciendo el producto vectorial obtenemos |
| </math> | | <center><math> |
| </center> | | \vec{L}_O = mR^2\dot{\theta}\,\vec{k}. |
| Resolviendo la primera ecuación obtenemos <math>\rho(t) </math>. Una vez conocida esta, la segunda ecuación
| | </math></center> |
| nos da la expresión de la fuerza de reacción vincular <math>\Phi(t) </math>.
| |
|
| |
|
| === Resolución de la ecuación diferencial === | | == Ecuación de movimiento == |
| | | El Teorema del Momento Cinético aplicado en el punto <math>O</math> dice |
| ==== Solución general ====
| | <center><math> |
| | | \dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} = \vec{M}_O |
| La ecuación diferencial para <math>\rho(t) </math> es
| | </math></center> |
| <center> | | El término de la derecha es el momento neto respecto de <math>O</math> de todas las fuerzas que |
| <math> | | actúan sobre la partícula. Tenemos |
| \ddot{\rho} = w^2\,\rho | | <center><math> |
| </math>
| | \begin{array}{l} |
| </center>
| | \overrightarrow{OP}\times\vec{N} = \vec{0},\\ |
| Puede comprobarse que las funciones <math>e^{\omega t} </math> y <math>e^{-\omega t} </math> son solución de esta
| | \overrightarrow{OP}\times\vec{F}_k = kR^2\,\mathrm{sen}\,\theta\,\vec{k} = mgR\,\mathrm{sen}\,\theta\,\vec{k}. |
| ecuación. Por tanto, la solución general es de la forma
| |
| <center>
| |
| <math>
| |
| \rho(t) = A\,e^{\omega t} + B\,e^{\omega t}
| |
| </math> | |
| </center> | |
| Las constantes <math>A </math> y <math>B </math> se determinan a partir de las condiciones iniciales.
| |
| | |
| La solución general puede escribirse de una forma alternativa usando las definiciones del seno y coseno hiperbólicos
| |
| <center> | |
| <math> | |
| \cosh(\alpha) = \dfrac{e^{\alpha} + e^{-\alpha}}{2} \qquad\qquad \mathrm{senh}(\alpha) = \dfrac{e^{\alpha} - e^{-\alpha}}{2} | |
| </math>
| |
| </center>
| |
| | |
| De esta forma la solución general se puede escribir
| |
| <center>
| |
| <math>
| |
| \rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t)
| |
| </math>
| |
| </center>
| |
| | |
| ==== Condiciones iniciales ====
| |
| | |
| Vamos a suponer que en el instante inicial el tubo es paralelo al eje <math>OX </math> y la partícula está situada
| |
| a una distancia <math>\rho_0 </math> del origen. Eso nos da una condición inicial sobre la posición
| |
| <center>
| |
| <math>
| |
| \rho(0) = \rho_0\,
| |
| </math>
| |
| </center>
| |
| Al empezar a girar el tubo, en un primer momento la partícula gira con él, por lo que la velocidad no tiene componente
| |
| radial. Así pues,
| |
| <center>
| |
| <math>
| |
| \dot{\rho}(0)=0
| |
| </math>
| |
| </center>
| |
| Determinamos las constantes <math>a </math> y <math>b </math> a partir de estas condiciones iniciales
| |
| <center>
| |
| <math>
| |
| \begin{array}{lclcl}
| |
| \rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t) &\to& \rho(0)=a=\rho_0 &\to& a = \rho_0 \\ &&&& \\
| |
| \dot{\rho}(t) = a\,\omega\,\mathrm{senh}(\omega t) + b\,\omega\,\cosh(\omega t) &\to& \dot{\rho}(0)=b\,\omega=0 &\to& b= 0 | |
| \end{array} | | \end{array} |
| </math> | | </math></center> |
| </center> | | El primer primer vectorial es nulo pues los dos vectores son paralelos. En el segundo hemos usado |
| | que, según el enunciado, <math>k=mg/R</math>. El momento neto es |
| | <center><math> |
| | \vec{M}_O = \overrightarrow{OP}\times\vec{F}_k = mgR\,\mathrm{sen}\,\theta\,\vec{k}. |
| | </math></center> |
|
| |
|
| Así pues, la evolución en el tiempo de la posición de la partícula, expresada en coordenadas polares, viene dada por
| | La derivada del momento cinético es |
| las funciones
| | <center><math> |
| <center>
| | \dot{\vec{L}}_O = mR^2\ddot{\theta}\,\vec{k}. |
| <math>
| | </math></center> |
| \rho(t) = \rho_0\cosh(\omega t) \qquad \qquad \theta(t) = \omega t
| | Por tanto la ecuación de movimiento es |
| </math>
| | <center><math> |
| </center>
| | \ddot{\theta} = \dfrac{g}{R}\,\mathrm{sen}\,\theta. |
| | | </math></center> |
| ==== Comportamiento asintótico ====
| |
| | |
| La función que da la evolución de la distancia de la partícula al origen puede escribirse | |
| <center>
| |
| <math>
| |
| \rho(t) = \rho_0\cosh(\omega t) = \dfrac{\rho_0}{2}\left(e^{\omega t} + e^{-\omega t}\right)
| |
| </math>
| |
| </center>
| |
| Al aumentar el tiempo, la primera exponencial crece, mientras que la segunda decrece. Vamos a ver que en un tiempo
| |
| corto esta segunda exponencial puede despreciarse respecto a la primera.
| |
| La escala de tiempo relevante es el tiempo que tarda el tubo en dar una vuelta. Si la velocidad angular es <math>\omega </math> este tiempo es
| |
| <center>
| |
| <math>
| |
| T = 2\pi/\omega
| |
| </math>
| |
| </center>
| |
| Vamos a ver el valor de las exponenciales para algunos valores de t
| |
| {| class='bordeado'
| |
| ! Tiempo
| |
| !<math>e^{\omega t} </math>
| |
| !<math>e^{-\omega t} </math>
| |
| !<math>e^{-\omega t}/e^{\omega t} </math>
| |
| |-
| |
| |0
| |
| |1
| |
| |1
| |
| |1
| |
| |-
| |
| |T/4
| |
| |4.81
| |
| |0.208
| |
| |0.043
| |
| |-
| |
| |T/2
| |
| |23.1
| |
| |0.043
| |
| |0.0019
| |
| |}
| |
| Es decir, cuando el tubo ha dado simplemente media vuelta, el valor de la segunda exponencial es sólo un 0.19% del valor
| |
| de la primera. Este factor se va haciendo más pequeño. Esto quiere decir que después de media vuelta del tubo,
| |
| el valor de la coordenada <math>\rho(t) </math> puede aproximarse con muy buena aproximación por
| |
| <center>
| |
| <math>
| |
| \rho(t) \simeq \dfrac{1}{2}\rho_0\,e^{\omega t}
| |
| </math>
| |
| </center>
| |
| | |
| === Fuerza ejercida por el tubo ===
| |
| La ecuación obtenida de las componentes angulares de la Segunda Ley de Newton nos da el valor de la fuerza
| |
| de reacción vincular
| |
| <center>
| |
| <math>
| |
| \vec{\Phi} = 2\,m\,\omega\,\dot{\rho}\,\vec{u}_{\theta}\simeq m\,\rho_0\,\omega^2e^{\omega t}\,\vec{u}_{\theta}
| |
| </math>
| |
| </center>
| |
| Hemos usado la aproximación asintótica de <math>\rho(t) </math>.
| |
| | |
| === Potencia desarrollada sobre la partícula ===
| |
| | |
| Dada una fuerza <math>\vec{\Phi} </math> actuando sobre una partícula, la potencia que le transfiere
| |
| en cada instante es
| |
| <center> | |
| <math> | |
| P = \vec{\Phi}\cdot\vec{v}
| |
| </math>
| |
| </center>
| |
| En nuestro caso, usando coordenadas polares tenemos
| |
| <center>
| |
| <math>
| |
| P = (\Phi\,\vec{u}_{\theta})\cdot(\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta})
| |
| =\rho\,\dot{\theta}\,\Phi
| |
| </math>
| |
| </center>
| |
| En este problema, y utilizando la expresión asintótica de <math>\rho(t) </math> tenemos
| |
| <center>
| |
| <math>
| |
| P \simeq \dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t}
| |
| </math>
| |
| </center>
| |
| | |
| === Trabajo realizado sobre la partícula entre <math>\rho=b </math> y <math>\rho=2b </math> ===
| |
| | |
| Vamos a calcular estre trabajo de dos formas, integrando la potencia en el tiempo e integrando
| |
| el trabajo a partir de su definición
| |
| | |
| ====Integración de la potencia ====
| |
| La potencia instantánea se define como
| |
| <center>
| |
| <math>
| |
| P(t) = \dfrac{\mathrm{d}W}{\mathrm{d}t} \Rightarrow \mathrm{d}W = P(t)\,\mathrm{d}t
| |
| </math>
| |
| </center>
| |
| Como tenemos la expresión de la potencia instantánea en función del tiempo, tenemos que hacer la integral
| |
| <center>
| |
| <math>
| |
| W_{\rho=b}^{\rho=2b} = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t
| |
| </math>
| |
| </center>
| |
| donde <math>t_b </math> y <math>t_{2b} </math> son los instantes de tiempo en los cuales el valor
| |
| de <math>\rho(t) </math> es <math>b </math> y <math>2b </math>, respectivamente. Para determinar
| |
| estos valores usamos la expresión asintótica de <math>\rho(t) </math>
| |
| <center>
| |
| <math>
| |
| \begin{array}{lcl}
| |
| \rho(t_b) = \dfrac{1}{2}\rho_0\,e^{\omega t_b}=b & \to & t_b = \dfrac{1}{\omega}\ln\left(\dfrac{2b}{\rho_0}\right)
| |
| \\ \\
| |
| \rho(t_{2b}) = \dfrac{1}{2}\rho_0\,e^{\omega t_{2b}}=2b & \to & t_{2b} = \dfrac{1}{\omega}\ln\left(\dfrac{4b}{\rho_0}\right)
| |
| \end{array}
| |
| </math>
| |
| </center>
| |
| Ahora podemos hacer la integral
| |
| <center>
| |
| <math>
| |
| \begin{array}{ll}
| |
| W_{\rho=b}^{\rho=2b}& = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t\\ &\\
| |
| & = \int\limits_{t_b}^{t_{2b}}\dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t}\,\mathrm{d}t\\
| |
| &\\
| |
| & = \dfrac{1}{2}m\,\rho_0^2\,\omega^3\int\limits_{t_b}^{t_{2b}}\,e^{2\omega t}\,\mathrm{d}t\\
| |
| &\\
| |
| & = \dfrac{1}{4}m\,\rho_0^2\,\omega^2\left[e^{2\omega t}\right]_{t_b}^{t_{2b}}
| |
| \end{array}
| |
| </math>
| |
| </center>
| |
| Tenemos
| |
| <center>
| |
| <math>
| |
| e^{2\omega t_b} = e^{2\ln\left(2b/\rho_0\right)} = \left(e^{\ln\left(2b/\rho_0\right)}\right)^2= \left(\dfrac{2b}{\rho_0}\right)^2
| |
| </math>
| |
| </center>
| |
| Operando igual para <math>e^{2\omega t_{2b}} </math> obtenemos para el trabajo
| |
| <center>
| |
| <math>
| |
| W_{\rho=b}^{\rho=2b} = 3\,m\,b^2\,\omega^2
| |
| </math>
| |
| </center>
| |
| | |
| ==== Integración de la definición de trabajo ====
| |
| Al realizar un desplazamiento diferencial <math>\mathrm{d}\vec{r} </math> el trabajo realizado
| |
| por la fuerza de reacción vincular es
| |
| <center>
| |
| <math>
| |
| \mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r}
| |
| </math>
| |
| </center>
| |
| El desplazamiento <math>\mathrm{d}\vec{r} </math> es
| |
| <center>
| |
| <math>
| |
| \mathrm{d}\vec{r} = \vec{v}\,\mathrm{d}t = (\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta})\,\mathrm{d}t
| |
| </math>
| |
| </center>
| |
| Una derivada es un cociente entre dos incrementos muy pequeños. Podemos hacer entonces
| |
| <center>
| |
| <math>
| |
| \dot{\rho}\,\mathrm{d}t = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho
| |
| \qquad\qquad
| |
| \dot{\theta}\,\mathrm{d}t = \dfrac{\mathrm{d}\theta}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\theta
| |
| </math> | |
| </center> | |
| Entonces el desplazamiento diferencial se puede expresar en función de las variaciones infinitesimales de <math>\rho </math>
| |
| y <math>\theta </math>
| |
| <center>
| |
| <math>
| |
| \mathrm{d}\vec{r} = \mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta}
| |
| </math>
| |
| </center>
| |
| Entonces el trabajo realizado por la fuerza de reacción vincular en un tiempo <math>\mathrm{d}t </math> es
| |
| <center> | |
| <math> | |
| \mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r} = (\Phi\,\vec{u}_{\theta})\cdot(\mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta}) = \Phi\,\rho\,\mathrm{d}\theta = 2\,m\,\omega\,\rho\,\dot{\rho}\,\mathrm{d}\theta | |
| </math>
| |
| </center>
| |
| Utilizando otra vez la idea de que la derivada es un cociente tenemos
| |
| <center>
| |
| <math>
| |
| \dot{\rho}\,\mathrm{d}\theta = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho\dfrac{\mathrm{d}\theta}{\mathrm{d}t} =
| |
| \mathrm{d}\rho\,\omega
| |
| </math>
| |
| </center>
| |
| Por tanto el trabajo infinitesimal es
| |
| <center>
| |
| <math>
| |
| \mathrm{d}W = 2\,m\,\omega^2\,\rho\,\mathrm{d}\rho
| |
| </math>
| |
| </center>
| |
| Ahora podemos calcular el trabajo en función del cambio en la coordenada radial
| |
| <center>
| |
| <math>
| |
| W_{\rho=b}^{\rho=2b} = \int\limits_b^{2b}2\,m\,\omega^2\,\rho\,\mathrm{d}\rho= m\,\omega^2\,\left[\rho^2\right]_b^{2b}
| |
| =3\,m\,b^2\,\omega^2
| |
| </math> | |
| </center> | |
| Obtenemos el mismo resultado que con el método anterior.
| |
|
| |
|
| === Variación de la energía cinética ===
| | [[Categoría:Problemas de examen]] |
| La energía cinética en cada instante es
| | [[Categoría:Problemas de examen de F1 GIC]] |
| <center>
| | [[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]] |
| <math>
| | [[Categoría:Problemas de Cinética de la partícula]] |
| T = \dfrac{1}{2}m\,v^2 = \dfrac{m}{2}\left(\dot{\rho}^2+ \rho^2\dot{\theta}^2\right)
| |
| \simeq
| |
| \dfrac{m\,\rho_0^2\,\omega^2}{4}e^{2\omega t}
| |
| </math>
| |
| </center>
| |
| donde hemos usado la solución asintótica. Como tenemos los instantes de tiempo que corresponden a <math>\rho=b </math>
| |
| y <math>\rho=2b </math>, podemos calcular la variación de energía cinética
| |
| <center>
| |
| <math>
| |
| \Delta T = T(t_{2b}) - T(t_b) = \dfrac{m}{2}\left(8\,b^2\,\omega^2 - 2\,b^2\,\omega^2\right) = 3\,m\,b^2\,\omega^2
| |
| </math>
| |
| </center>
| |
| Podemos comprobar que la variación de la energía cinética es igual al trabajo realizado por la fuerza de reacción vincular. Se
| |
| verifica así el teorema de las fuerzas vivas.
| |