(Página creada con «== Enunciado == right Una partícula <math>P</math>, de masa <math>m</math>, se mueve en el plano horizontal sometida a la acción de dos resortes elásticos ideales e idénticos, de constante <math>k</math> y longitud natural nula. Los puntos de anclaje son <math>C(-d,0)</math> y <math>D(d,0)</math>, respectivamente #Escribe la ecuación diferencial que determina el movimiento de la partícula. #Si las condiciones iniciale…»)
 
(Página creada con «= Enunciado = right Una partícula de masa <math>m</math> está engarzada en un semiaro de radio <math>R</math>. Un muelle de constante elástica <math>k=mg/R</math> y longitud natural nula conecta la partícula y el punto <math>A</math> del semiaro. La gravedad no actúa. #Dibuja el diagrama de fuerzas de la partícula. #Escribe la expresión que da el momento cinético de la partícula respecto al punto <…»)
 
Línea 1: Línea 1:
== Enunciado ==
= Enunciado =
[[Imagen:F1A_GIA_dos_muelles_enunciado.png|right]]
[[File:F1GIERM-particula-aro-muelle-cinetico-enunciado.png|right]]
Una partícula <math>P</math>, de masa <math>m</math>, se mueve en el plano horizontal sometida a la acción de dos resortes elásticos ideales e idénticos, de constante <math>k</math> y longitud natural nula. Los puntos de anclaje son <math>C(-d,0)</math> y <math>D(d,0)</math>, respectivamente
Una partícula de masa <math>m</math> está engarzada en un semiaro de radio <math>R</math>. Un muelle de  
#Escribe la ecuación diferencial que determina el movimiento de la partícula.
constante elástica <math>k=mg/R</math> y longitud natural nula conecta la partícula y el punto <math>A</math>
#Si las condiciones iniciales son <math>\vec{r}(0)=a\,\vec{\imath}</math> y <math>\vec{v}(0)=v_0\,\vec{\jmath}</math>, encuentra las expresiones que dan la posición y la velocidad de la partícula en todo instante de tiempo.
del semiaro. La gravedad no actúa.
#Determina, para todo instante de tiempo, el momento cinético, <math>\vec{L}_O</math>, de la partícula <math>P</math> respecto al origen de coordenadas <math>O</math>, así como su energía mecánica, <math>E</math>. ¿Qué  teoremas de conservación explican las propiedades de estas magnitudes en este problema?
#Dibuja el diagrama de fuerzas de la partícula.
#Escribe la expresión que da el momento cinético de la partícula respecto al punto <math>O</math>.
#Aplicando el Teorema del Momento Cinético, encuentra la ecuación de movimiento de la partícula.


== Solución ==
= Solución =
===Ecuación del movimiento===


La expresión que da la ecuación del movimiento es la Segunda Ley de Newton
== Diagrama de fuerzas ==
[[File:F1GIERM-particula-aro-muelle-cinetico-fuerzas.png|right]]
La figura de la derecha muestra las fuerzas que actúan sobre la partícula. La fuerza vincular
<math>\vec{N}</math> es perpendicular al aro, es decir, radial. La fuerza del muelle apunta hacia
el punto de anclaje del muelle <math>A</math>. Las expresiones de estas fuerzas son
<center><math>
<center><math>
  m\vec{a} = \sum\limits_{i=1}^n\vec{F}_i
\begin{array}{l}
\vec{N} = N\cos\theta\,\vec{\imath} + N\,\mathrm{sen}\,\theta\,\vec{\jmath},\\
\vec{F}_k = -k\overrightarrow{AP} =
-k(\overrightarrow{OP}-\overrightarrow{OA})
= -kR(1+\cos\theta)\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath}.
\end{array}
</math></center>
</math></center>
donde, <math>m</math> es la masa de la partícula, <math>\vec{a}</math> su aceleración respecto de un sistema
Hemos usado los vectores
inercial y <math>\vec{F}_i</math> las fuerzas que actúan sobre ella.
 
Usamos coordenadas cartesianas y el sistema de ejes de la figura. Al ser un movimiento
plano podemos ignorar la componente de los vectores en el eje <math>OZ</math>.  El vector de posición,
la velocidad y la aceleración de la partícula son
<center><math>
<center><math>
  \left.
\begin{array}{l}
  \begin{array}{l}
\overrightarrow{OP} = R\cos\theta\,\vec{\imath} + R\,\mathrm{sen}\,\theta\,\vec{\jmath},\\
    \vec{r}(t) = x(t)\,\vec{\imath} + y(t)\,\vec{\jmath} \\ \\
\overrightarrow{OA} = - R\,\vec{\imath}.
    \vec{v}(t) = \dot{x}\,\vec{\imath} + \dot{y}\,\vec{\jmath} \\ \\
\end{array}
    \vec{a}(t) = \ddot{x}\,\vec{\imath} + \ddot{y}\,\vec{\jmath}
  \end{array}
  \right.
</math></center>
</math></center>


En este problema, considerando que el movimiento se desarrolla sobre un plano, la
 
partícula está sometida a dos fuerzas, la de cada uno de los muelles. (Si hiciéramos el
== Momento cinético ==
experimento sobre una mesa, el peso de la partícula se vería compensado en cada instante
El momento cinético respecto del punto <math>O</math> es
por la f.r.v. de la mesa, con lo que no afectan al movimiento). Como son dos resortes
ideales, si el vector de posición de la partícula es <math>\vec{r}(t)</math>, la fuerza que ejerce
sobre ella cada uno de los muelles es
<center><math>
<center><math>
  \vec{F}_C = -k(\vec{r}-\vec{r}_C) \qquad \qquad \vec{F}_D = -k(\vec{r}-\vec{r}_D)
\vec{L}_O = \overrightarrow{OP}\times(m\vec{v}).
</math></center>
</math></center>
Los vectores <math>\vec{r}_C</math> y <math>\vec{r}_D</math> son los vectores de posición de los puntos de
El vector velocidad es
anclaje de los muelles. Si escogemos el sistema de ejes de la figura estos vectores son
<center><math>
<center><math>
  \vec{r}_C =   -d\,\vec{\imath} \qquad \qquad \vec{r}_D =  d\,\vec{\imath}
\vec{v}=\dot{\overrightarrow{OP}} = -R\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} +
R\dot{\theta}\cos\theta\,\vec{\jmath}.
</math></center>
</math></center>
En la coordenadas cartesianas que hemos elegido la expresión de las fuerzas es
Haciendo el producto vectorial obtenemos
<center><math>
<center><math>
  \left.
\vec{L}_O = mR^2\dot{\theta}\,\vec{k}.
  \begin{array}{l}
    \vec{F}_C = -k\left( (x+d)\,\vec{i} + y\,\vec{\jmath}\right)\\
    \vec{F}_D = -k\left( (x-d)\,\vec{i} + y\,\vec{\jmath}\right)
  \end{array}
  \right.
</math></center>
</math></center>


Podemos escribir la ecuación del movimiento.
== Ecuación de movimiento ==
<center><math>
El Teorema del Momento Cinético aplicado en el punto <math>O</math> dice
  m\,\vec{a} = \vec{F}_C + \vec{F}_D = -k(\vec{r}_C-\vec{r}) -k(\vec{r}_D-\vec{r}) =
  -2k\,\vec{r} -k(\vec{r}_C+\vec{r}_D)
</math></center>
Como podemos ver en la figura y en la expresión de los vectores, se cumple
<math>\vec{r}_C+\vec{r}_D=\vec{0}</math>.  La ecuación se puede escribir
<center><math>
<center><math>
  \ddot{\vec{r}} = -\dfrac{2k}{m}\vec{r}
\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} = \vec{M}_O
</math></center>
</math></center>
Esto es la ecuación de un movimiento armónico. La podemos escribir como
El término de la derecha es el momento neto respecto de <math>O</math> de todas las fuerzas que
<center><math>
actúan sobre la partícula. Tenemos
  \ddot{\vec{r}} = -\omega^2\vec{r} \qquad \qquad w = \sqrt{\dfrac{2k}{m}}
<center><math>
</math></center>
\begin{array}{l}
La solución general es una superposición de senos y cosenos. Lo único nuevo en esta ecuación es que los coeficientes de la combinación lineal son vectores en vez de escalares. Es decir, la solución es de la forma
\overrightarrow{OP}\times\vec{N} = \vec{0},\\
<center><math>
\overrightarrow{OP}\times\vec{F}_k = kR^2\,\mathrm{sen}\,\theta\,\vec{k} = mgR\,\mathrm{sen}\,\theta\,\vec{k}.
  \vec{r}(t) = \vec{A}\cos(\omega t) + \vec{B}\,\mathrm{sen}\,(\omega t)
\end{array}
</math></center>
</math></center>
y la velocidad se obtiene derivando respecto al tiempo
El primer primer vectorial es nulo pues los dos vectores son paralelos. En el segundo hemos usado
<center><math>
que, según el enunciado, <math>k=mg/R</math>. El momento neto es
  \vec{v}(t) = -\omega\,\vec{A}\,\mathrm{sen}\,(\omega t)\vec{\imath} + \omega\,\vec{B}\cos(\omega
  t)\vec{\jmath}
</math></center>
 
===Solución concreta===
El enunciado nos da las condiciones iniciales
<center><math>
  \vec{r}(0) = a\,\vec{\imath} \qquad \qquad \vec{v}(0) = v_0\,\vec{\jmath}
</math></center>
Para aplicarlas evaluamos en <math>t=0</math> las expresiones de <math>\vec{r}(t)</math> y <math>\vec{v}(t)</math> obtenidas en el apartado anterior
<center><math>
  \left.
  \begin{array}{l}
    \vec{r}(0) = \vec{A} = a\,\vec{\imath} \Longrightarrow \vec{A} = a\,\vec{\imath} \\ \\
    \vec{v}(0) = \omega\,\vec{B} \Longrightarrow \vec{B} = \dfrac{v_0}{\omega}\vec{\jmath}
  \end{array}
  \right.
</math></center>
Las expresiones de la posición y la velocidad en cada instante son
<center><math>
  \left.
  \begin{array}{l}
    \vec{r}(t) = \vec{\imath}\,a\cos(\omega t) + \vec{\jmath}\,\dfrac{v_0}{\omega}\,\mathrm{sen}\,(\omega t)\\
      \\
    \vec{v}(t) = -\vec{\imath}\,a\omega\,\mathrm{sen}\,(\omega t) + \vec{\jmath}\,v_0\cos(\omega t)
  \end{array}
  \qquad \qquad
  \omega = \sqrt{\dfrac{2k}{m}}
  \right.
</math></center>
 
===Momento cinético===
El momento cinético respecto al origen en cada instante es
<center><math>
  \vec{L}_O = \overrightarrow{OP}\times\vec{p} = \vec{r}\times(m\vec{v}) = m\,a\,v_0\,\vec{k}
</math></center>
Vemos que no depende del tiempo. Eso se debe a que la fuerza resultante sobre la partícula es central respecto al punto <math>O</math>.  Entonces
<center><math>
  \frac{\displaystyle \mathrm{d}\vec{L}_O}{\displaystyle\mathrm{d} t} = \vec{M}_O =
  \overrightarrow{OP}\times\vec{F}=\vec{r}\times(-2k\,\vec{r}) = \vec{0}
</math></center>
 
===Energía cinética===
La energía cinética es
<center><math>
  T = \dfrac{1}{2}m\,v^2 = \dfrac{m}{2}\left( a^2\omega^2\,\mathrm{sen}\,^2(\omega t) +
  v_0^2\cos^2(\omega t) \right)
</math></center>
No permanece constante pues la velocidad de la partícula cambia con el tiempo.
 
Por otro lado, la energía potencial asociada a los muelles es
<center><math>
  U = \dfrac{1}{2}k|\vec{r}-\vec{r}_C|^2 + \dfrac{1}{2}k|\vec{r}-\vec{r}_D|^2
</math></center>
Tenemos
<center><math>
  \left.
  \begin{array}{lll}
    \vec{r}-\vec{r}_C = (x+d)\,\vec{\imath} + y\,\vec{\jmath} &\Longrightarrow &
|\vec{r}-\vec{r}_C|^2 = (x+d)^2+y^2 \\ \\
    \vec{r}-\vec{r}_D = (x-d)\,\vec{\imath} + y\,\vec{\jmath} &\Longrightarrow &
|\vec{r}-\vec{r}_D|^2 = (x-d)^2+y^2
  \end{array}
  \right.
</math></center>
Entonces
<center><math>
<center><math>
  U = \dfrac{k}{2}\left( |\vec{r}-\vec{r}_C|^2 + |\vec{r}-\vec{r}_D|^2\right) =
\vec{M}_O = \overrightarrow{OP}\times\vec{F}_k = mgR\,\mathrm{sen}\,\theta\,\vec{k}.
  k(x^2+y^2) + kd^2=
  k\left[ a^2\cos^2(\omega t) + \dfrac{v_0^2}{\omega^2}\,\mathrm{sen}\,^2(\omega t) \right] + kd^2
</math></center>
</math></center>
Tampoco es constante pues la elongación de los muelles cambia en el tiempo.


La energía mecánica es la suma de la cinética y la potencial
La derivada del momento cinético es
<center><math>
<center><math>
  E = T + U = \dfrac{1}{2}m\,v_0^2 + k\,(a^2+d^2)
\dot{\vec{L}}_O = mR^2\ddot{\theta}\,\vec{k}.
</math></center>
</math></center>
La energía mecánica si es constante en el tiempo, pues no hay fuerzas no conservativas
Por tanto la ecuación de movimiento es
actuando sobre la partícula. Podríamos haber calculado el valor de la energía mecánica a
partir de las condiciones iniciales
<center><math>
<center><math>
  \left.
\ddot{\theta} = \dfrac{g}{R}\,\mathrm{sen}\,\theta.
  \begin{array}{lll}
    \vec{v}(0) = v_0\,\vec{\jmath} & \Longrightarrow & T(t=0) = \dfrac{mv_0^2}{2} \\ && \\
    \vec{r}(0) = a\,\vec{\imath} & \Longrightarrow &
    \left\{
    \begin{array}{l}
      U_C(t=0) = \dfrac{k}{2}|\vec{r}(0)-\vec{r}_C|^2 = \dfrac{k}{2}\left( a+d \right)^2 \\ \\
      U_D(t=0) = \dfrac{k}{2}|\vec{r}(0)-\vec{r}_D|^2 = \dfrac{k}{2}\left( a-d \right)^2
    \end{array}
    \right.
  \end{array}
  \right.
</math></center>
</math></center>
Sumando obtenemos
<center>
<math>
\begin{array}{lcl}
  T(t=0) + U_C(t=0) + U_D(t=0) =  \dfrac{1}{2}m\,v_0^2 + k\,(a^2+d^2) = E
\end{array}
</math>
</center>


[[Categoría:Dinámica del punto material|1]]
[[Categoría:Problemas de examen]]
[[Categoría:Física I (G.I.A.)]]
[[Categoría:Problemas de examen de F1 GIC]]
[[Categoría:Física I (G.I.T.I.)]]
[[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]]
[[Categoría:Problemas de Cinética de la partícula]]

Revisión actual - 14:29 31 oct 2023

Enunciado

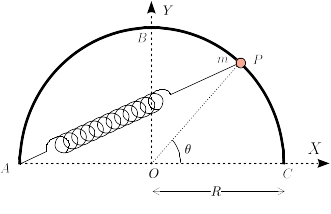
Una partícula de masa está engarzada en un semiaro de radio . Un muelle de constante elástica y longitud natural nula conecta la partícula y el punto del semiaro. La gravedad no actúa.

  1. Dibuja el diagrama de fuerzas de la partícula.
  2. Escribe la expresión que da el momento cinético de la partícula respecto al punto .
  3. Aplicando el Teorema del Momento Cinético, encuentra la ecuación de movimiento de la partícula.

Solución

Diagrama de fuerzas

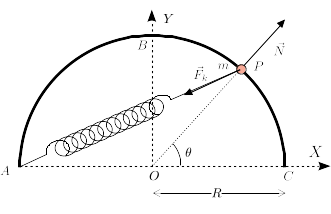
La figura de la derecha muestra las fuerzas que actúan sobre la partícula. La fuerza vincular es perpendicular al aro, es decir, radial. La fuerza del muelle apunta hacia el punto de anclaje del muelle . Las expresiones de estas fuerzas son

Hemos usado los vectores


Momento cinético

El momento cinético respecto del punto es

El vector velocidad es

Haciendo el producto vectorial obtenemos

Ecuación de movimiento

El Teorema del Momento Cinético aplicado en el punto dice

El término de la derecha es el momento neto respecto de de todas las fuerzas que actúan sobre la partícula. Tenemos

El primer primer vectorial es nulo pues los dos vectores son paralelos. En el segundo hemos usado que, según el enunciado, . El momento neto es

La derivada del momento cinético es

Por tanto la ecuación de movimiento es

Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_sometida_a_la_acción_de_dos_muelles_(GIA)&oldid=1223»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Partícula_sometida_a_la_acción_de_dos_muelles_(GIA)&oldid=1223»