Diferencia entre las páginas «Archivo:MR disco cavidad muelle torsion enunciado.png» y «Disco rodando en cavidad con muelle de torsión MR Dic 2016/17»
Sin resumen de edición |
(Página creada con «= Enunciado = right Un disco de radio <math>R</math> y masa <math>m</math> (sólido "2") rueda sin deslizar sobre una superficie circular cóncava (sólido "1") de radio <math>3R</math>. En el centro del disco se articula una barra (sólido "0") de masa despreciable y longitud <math>2R</math>. El otro extremo de la barra se articula en un punto fijo <math>O</math>. La barra está conectada a su vez a un resorte…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | |||
[[Imagen:MR_disco_cavidad_muelle_torsion_enunciado.png|right]] | |||
Un disco de radio <math>R</math> y masa <math>m</math> (sólido "2") rueda sin deslizar sobre | |||
una superficie circular cóncava (sólido "1") de radio <math>3R</math>. En el centro del | |||
disco se articula una barra (sólido "0") de masa despreciable y longitud <math>2R</math>. El otro | |||
extremo de la barra se articula en un punto fijo <math>O</math>. La barra está conectada | |||
a su vez a un resorte de torsión en el punto <math>O</math>. Este resorte ejerce | |||
un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él | |||
se puede expresar como <math>U_k = k \phi^2</math>, siendo <math>k</math> una constante. | |||
#Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre <math>\dot{\phi}</math> y <math>\dot{\psi}</math>?. | |||
#Calcula la energía cinética del disco y su energía potencial. | |||
#Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo <math>\phi</math> es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación. | |||
#Estando el disco en reposo y con <math>\phi=0</math>, se aplica al centro del disco una percusión <math>\hat{\vec{F}} = \hat{F}_0\,\vec{\jmath}_0</math>. Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje <math>OY_1</math>. | |||
= Solución = | |||
== Reducciones cinemáticas == | |||
=== Movimiento {01} === | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \dot{\phi}\,\vec{k}_1, | |||
\qquad\qquad | |||
\vec{v}^{\,O}_{01} = \vec{0}. | |||
</math> | |||
</center> | |||
Calculamos también la velocidad del centro de masas | |||
<center> | |||
<math> | |||
\vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG}= | |||
2R\dot{\phi}\,\vec{\jmath}_0. | |||
</math> | |||
</center> | |||
Hemos usado que | |||
<center> | |||
<math> | |||
\overrightarrow{OG} = 2R\,\vec{\imath}_0. | |||
</math> | |||
</center> | |||
=== Movimiento {20} === | |||
Del dibujo vemos | |||
<center> | |||
<math> | |||
\vec{\omega}_{20} = -\dot{\psi}\,\vec{k}_1, | |||
\qquad\qquad | |||
\vec{v}^{\,G}_{20} = \vec{0}. | |||
</math> | |||
</center> | |||
=== Movimiento {21} === | |||
Usando la composición {21} = {20} + {01} tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = (\dot{\phi}-\dot{\psi})\,\vec{k}_1, | |||
\\ | |||
\\ | |||
\vec{v}^{\,G}_{21} = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01} = 2R\dot{\phi}\,\vec{\jmath}_1. | |||
\end{array} | |||
</math> | |||
</center> | |||
La relación entre las derivadas de los ángulos se obtiene imponiendo que, al ser una rodadura sin deslizamiento, se cumple | |||
<center> | |||
<math> | |||
\vec{v}^{\,D}_{21} = \vec{0}. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,D}_{21} = \vec{v}^{\,G}_{21} + \vec{\omega}_{21}\times\overrightarrow{GD} | |||
= | |||
(2R\dot{\phi} +(\dot{\phi}-\dot{\psi})R)\,\vec{\jmath}_0 = \vec{0} | |||
\Longrightarrow | |||
\dot{\psi} = 3\dot{\phi}. | |||
</math> | |||
</center> | |||
== Energía cinética y potencial del disco == | |||
Al ser un movimiento plano la energía cinética es | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}I|\vec{\omega}_{21}|^2 = | |||
3mR^2\dot{\phi}^2. | |||
</math> | |||
</center> | |||
El momento de inercia del disco es <math>I=mR^2/2</math>. | |||
Tenemos energía potencial gravitatoria y elástica. Para la gravitatoria elegimos como referencia la línea <math>y_1=0</math>, por tanto | |||
<center> | |||
<math> | |||
U_g = -2mgR\cos\phi. | |||
</math> | |||
</center> | |||
El enunciado nos da la energía potencial elástica del muelle de torsión | |||
<center> | |||
<math> | |||
U_k = k\phi^2 | |||
</math> | |||
</center> | |||
Entonces la energía potencial total es | |||
<center> | |||
<math> | |||
U = U_g + U_k = k\phi^2 - 2mgR\cos\phi. | |||
</math> | |||
</center> | |||
La energía mecánica es | |||
<center> | |||
<math> | |||
E = T + U = 3mR^2\dot{\phi}^2 + k\phi^2 - 2mgR\cos\phi. | |||
</math> | |||
</center> | |||
== Lagrangiana y ecuación de movimiento == | |||
La función de Lagrange es | |||
<center> | |||
<math> | |||
L = T - U = 3mR^2\dot{\phi}^2 - k\phi^2 + 2mgR\cos\phi. | |||
</math> | |||
</center> | |||
La ecuación de movimiento es | |||
<center> | |||
<math> | |||
\dfrac{\mathrm{d}\,}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\phi}}\right) - \dfrac{\partial L}{\partial\phi} = 0 | |||
</math> | |||
</center> | |||
Haciendo las derivadas obtenemos | |||
<center> | |||
<math> | |||
3mR^2\ddot{\phi} + mgR\mathrm{sen}\,\phi + k\phi = 0. | |||
</math> | |||
</center> | |||
Para ángulos pequeños podemos sustituir el seno por el primer término del desarrollo de Taylor | |||
<center> | |||
<math> | |||
\mathrm{sen}\,\phi = \phi + O(\phi^3), | |||
</math> | |||
</center> | |||
y podemos escribir la ecuación diferencial como | |||
<center> | |||
<math> | |||
\ddot{\phi} = - \dfrac{mgR+k}{3mR^2}\,\phi. | |||
</math> | |||
</center> | |||
Esta es la ecuación de movimiento de un oscilador armónico con frecuencia angular <math>\omega = \sqrt{(mgR+k)/3mR^2}</math> y período | |||
<center> | |||
<math> | |||
T_{\omega} = \dfrac{2\pi}{\omega} = | |||
2\pi\sqrt{\dfrac{3mR^2}{mgR+k}}. | |||
</math> | |||
</center> | |||
== Percusión == | |||
La ecuación de Lagrange percusiva es | |||
<center> | |||
<math> | |||
\Delta p_{\phi} = \hat{Q}_{\phi} | |||
</math> | |||
</center> | |||
El momento generalizado es | |||
<center> | |||
<math> | |||
p_{\phi} = \dfrac{\partial L}{\partial\dot{\phi}} = 6mR^2\dot{\phi} | |||
</math> | |||
</center> | |||
y por tanto | |||
<center> | |||
<math> | |||
\Delta p_{\phi} = 6mR^2(\phi(0^+) -\phi(0^-)) = 6mR^2\dot{\phi}(0^+). | |||
</math> | |||
</center> | |||
Para la percusión generalizada tenemos | |||
<center> | |||
<math> | |||
\hat{Q}_{\phi} = \hat{\vec{F}}\cdot\dfrac{\partial\vec{v}^{\,G}_{21}}{\partial\dot{\phi}} | |||
= | |||
\left(\hat{F}_0\,\vec{\jmath}_0\right)\cdot\left(2R\,\vec{\jmath}_1\right) = | |||
2\hat{F}_0R\,\vec{\jmath}_0\cdot\vec{\jmath}_1. | |||
</math> | |||
</center> | |||
Ahora bien, en el instante inicial <math>\phi(0)=0</math>, los ejes <math>OY_1</math> y <math>OY_0</math> coinciden y se tiene <math>\vec{\jmath}_1(0) = \vec{\jmath}_0(0)</math>. Por tanto | |||
<center> | |||
<math> | |||
\hat{Q}_{\phi} = | |||
2\hat{F}_0R. | |||
</math> | |||
</center> | |||
Por tanto la velocidad generalizada después de la percusión es | |||
<center> | |||
<math> | |||
\dot{\phi}(0^+) = \dfrac{\hat{F}_0}{3mR}. | |||
</math> | |||
</center> | |||
Durante la percusión <math>\phi=0</math>. Así pues, | |||
la energía mecánica justo después de la percusión es | |||
<center> | |||
<math> | |||
E(0^+) = \dfrac{\hat{F}^2_0}{3m} - 2mgR | |||
</math> | |||
</center> | |||
Para que el disco llegue arriba (<math>\phi=\pi/2)</math> con velocidad del centro de masas la energía mecánica final debe ser | |||
<center> | |||
<math> | |||
E = k\dfrac{\pi^2}{4}. | |||
</math> | |||
</center> | |||
Por tanto la condición es | |||
<center> | |||
<math> | |||
\hat{F}_0 \geq \sqrt{3m\,\left(2mgR + \dfrac{\pi^2}{4}k\right)}. | |||
</math> | |||
</center> | |||
[[Categoría:Problemas de mecánica analítica]] | |||
[[Categoría:Problemas de Dinámica Analítica]] | |||
[[Categoría:Problemas de Dinámica Impulsiva]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | |||
Revisión actual - 12:46 8 nov 2023
Enunciado
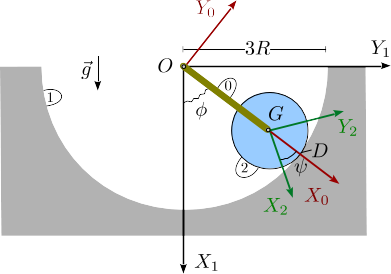
Un disco de radio y masa (sólido "2") rueda sin deslizar sobre una superficie circular cóncava (sólido "1") de radio . En el centro del disco se articula una barra (sólido "0") de masa despreciable y longitud . El otro extremo de la barra se articula en un punto fijo . La barra está conectada a su vez a un resorte de torsión en el punto . Este resorte ejerce un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él se puede expresar como , siendo una constante.
- Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre y ?.
- Calcula la energía cinética del disco y su energía potencial.
- Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación.
- Estando el disco en reposo y con , se aplica al centro del disco una percusión . Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje .
Solución
Reducciones cinemáticas
Movimiento {01}
Tenemos
Calculamos también la velocidad del centro de masas
Hemos usado que
Movimiento {20}
Del dibujo vemos
Movimiento {21}
Usando la composición {21} = {20} + {01} tenemos
La relación entre las derivadas de los ángulos se obtiene imponiendo que, al ser una rodadura sin deslizamiento, se cumple
Tenemos
Energía cinética y potencial del disco
Al ser un movimiento plano la energía cinética es
El momento de inercia del disco es .
Tenemos energía potencial gravitatoria y elástica. Para la gravitatoria elegimos como referencia la línea , por tanto
El enunciado nos da la energía potencial elástica del muelle de torsión
Entonces la energía potencial total es
La energía mecánica es
Lagrangiana y ecuación de movimiento
La función de Lagrange es
La ecuación de movimiento es
Haciendo las derivadas obtenemos
Para ángulos pequeños podemos sustituir el seno por el primer término del desarrollo de Taylor
y podemos escribir la ecuación diferencial como
Esta es la ecuación de movimiento de un oscilador armónico con frecuencia angular y período
Percusión
La ecuación de Lagrange percusiva es
El momento generalizado es
y por tanto
Para la percusión generalizada tenemos
Ahora bien, en el instante inicial , los ejes y coinciden y se tiene . Por tanto
Por tanto la velocidad generalizada después de la percusión es
Durante la percusión . Así pues, la energía mecánica justo después de la percusión es
Para que el disco llegue arriba ( con velocidad del centro de masas la energía mecánica final debe ser
Por tanto la condición es
Historial del archivo
Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.
| Fecha y hora | Miniatura | Dimensiones | Usuario | Comentario | |
|---|---|---|---|---|---|
| actual | 12:45 8 nov 2023 |  | 391 × 274 (33 kB) | Pedro (discusión | contribs.) |
No puedes sobrescribir este archivo.
Usos del archivo
Las siguientes páginas usan este archivo:













































