Diferencia entre las páginas «Disco sobre barra en forma de L (MR G.I.C.)» y «Deslizadera y disco rodando sin deslizar (MR G.I.C.)»
(Página creada con «= Enunciado = right El disco homogéneo de la figura (sólido "2") tiene masa <math>m</math> y radio <math>R</math>. Está conectado por su centro <math>G</math> con una estructura (sólido "0") formada por dos barras perpendiculares de masas despreciables y longitud <math>R</math> cada una. El disco puede rotar alrededor del eje <math>AG</math>, mientras que el sólido "0" puede rotar respecto a la línea <math>OA</math>. Se e…») |
(Página creada con «= Enunciado = right Un disco homogéneo (sólido "2") de masa <math>m</math> y radio <math>R</math> puede rotar alrededor de su centro <math>C</math>, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa <math>m</math> puede moverse a lo largo del eje <math>O_1Y_1</math>, de modo que en el punto de contacto <math>A</math> el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un m…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | = Enunciado = | ||
[[File: | [[File:MR_disco_deslizadera_enunciado.png|right]] | ||
Un disco homogéneo (sólido "2") de masa <math>m</math> y radio <math>R</math> puede rotar alrededor de su | |||
centro <math>C</math>, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa <math>m</math> | |||
puede moverse a lo largo del | |||
eje <math>O_1Y_1</math>, de modo que en el punto de contacto <math>A</math> el disco rueda sin deslizar sobre el | |||
sólido "0". La deslizadera está conectada a un muelle de constante elástica <math>k</math> y | |||
el | longitud natural <math>l_0</math>. El otro extremo del muelle está anclado en un punto fijo del eje | ||
<math> | <math>O_1X_1</math>, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura. | ||
que | |||
#¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales. | |||
#Calcula las energías cinética y potencial del sistema en función de sus grados de libertad. | |||
El | #Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento. | ||
sistema está sometido a la acción de la gravedad | #Se aplica sobre el disco un par de fuerzas externo <math>\vec{\tau} = \tau_0\cos(\omega t)\,\vec{k}_1</math>. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de <math>\omega</math> aparece una resonancia mecánica? | ||
#Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21} en | #Ahora no hay par aplicado. Se aplica una percusión <math>\vec{\hat{F}}=[\hat{F}_0, \hat{F}_0,0]_1</math> sobre el punto <math>B</math> del sólido "2". En el instante de la percusión se cumple <math>s(0)=l_0</math>, <math>\theta(0)=0</math>, <math>\dot{s}(0^-)=0</math>, <math>\dot{\theta}(0^-)=0</math>. Calcula el estado del sistema inmediatamente después de la percusión. | ||
# | |||
# | |||
= Solución = | = Solución = | ||
== Reducciones cinemáticas == | == Reducciones cinemáticas y grados de libertad == | ||
=== Movimiento {01} === | === Movimiento {01} === | ||
La | La deslizadera realiza un movimiento de traslación vertical. Tenemos | ||
<center> | <center> | ||
<math> | <math> | ||
\vec{v} | \begin{array}{ll} | ||
\ | \vec{v}_{01} = \dot{s}\,\vec{\jmath}_1, & \vec{\omega}_{01} = \vec{0} \\ | ||
\vec{ | \vec{a}_{01} = \ddot{s}\,\vec{\jmath}_1, & \vec{\alpha}_{01} = \vec{0} | ||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
No ponemos letras en la velocidad y aceleración pues es una traslación y son iguales en todos los puntos. | |||
=== Movimiento {21} === | |||
El disco hace una rotación con su centro fijo. Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{ | \begin{array}{ll} | ||
\vec{\alpha}_{ | \vec{v}^{\,C}_{21} = \vec{0}, & \vec{\omega}_{01} = -\dot{\theta}\,\vec{k}_1 \\ | ||
\vec{a}^{\,C}_{21} = \vec{0}, & \vec{\alpha}_{21} = -\ddot{\theta}\,\vec{k}_1 | |||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
=== Movimiento {20} === | === Movimiento {20} === | ||
Usamos las reglas de composición | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{v}^{\, | \begin{array}{l} | ||
\ | \vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = -\dot{\theta}\,\vec{k}_1\\ | ||
\vec{\omega}_{20} = \ | \vec{\alpha}_{20} = \vec{\alpha}_{21} - \vec{\alpha}_{01} - \vec{\omega}_{01}\times\vec{\omega}_{20} = -\ddot{\theta}\,\vec{k}_1\\ | ||
\vec{v}^{\,C}_{20} = \vec{v}^{\,C}_{21} - \vec{v}^{\,C}_{01} = -\dot{s}\,\vec{\jmath}_1\\ | |||
\vec{a}^{\,C}_{20} = \vec{a}^{\,C}_{21} - \vec{a}^{\,C}_{01} -2\vec{\omega}_{01}\times\vec{v}^{\,C}_{20} = -\ddot{s}\,\vec{\jmath}_1\\ | |||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
La | |||
=== Grados de libertad === | |||
La condición de rodadura sin deslizamiento impone una ligadura entre <math>s</math> y <math>\theta</math> | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{ | \vec{v}^{\,A}_{20} = \vec{0} | ||
\vec{\ | \Longrightarrow | ||
\vec{v}^{\,C}_{20} + \vec{\omega}_{20}\times\overrightarrow{CA} | |||
= | |||
(-\dot{s}+R\dot{\theta})\,\vec{\jmath}_1=\vec{0} | |||
\Longrightarrow | |||
\dot{s}=R\dot\theta | |||
</math> | </math> | ||
</center> | </center> | ||
Es decir, el sistema tiene un grado de libertad. Elegiremos <math>\{s\}</math> para describir el movimiento. | |||
=== | == Energía cinética y potencial == | ||
La energía cinética total es la suma de la energía cinética de cada sólido | |||
<center> | |||
<math> | |||
T = T_0 + T_2 | |||
</math> | |||
</center> | |||
La deslizadera tiene sólo energía cinética de traslación | |||
<center> | |||
<math> | |||
T_0 = \dfrac{1}{2}m|\vec{v}_{01}|^2 = \dfrac{1}{2}m\dot{s}^2 | |||
</math> | |||
</center> | |||
El disco tiene sólo energía cinética de rotación | |||
<center> | |||
<math> | |||
T_2 = \dfrac{1}{2}I_C|\vec{\omega}_{01}|^2 = \dfrac{1}{4}mR^2\dot{\theta}^2 = \dfrac{1}{4}m\dot{s}^2 | |||
</math> | |||
</center> | |||
La energía cinética total es | |||
<center> | |||
<math> | |||
T = T_0+T_2 = \dfrac{3}{4}m\dot{s}^2 | |||
</math> | |||
</center> | |||
La deslizadera tiene energía potencial y elástica. El centro del masas del disco no cambia su altura, por lo que su energía potencial gravitatoria es constante y no afecta a la dinámica del sistema. Podemos ignorarla. Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
U_{0g} = mgs\\ | |||
U_{0k} = \dfrac{1}{2}k(s-l_0)^2\\ | |||
U = U_{0g} + U_{0k} = mgs + \dfrac{1}{2}k(s-l_0)^2 | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
== Lagrangiana y ecuaciones de Euler == | |||
La función de Lagrange es | |||
<center> | <center> | ||
<math> | <math> | ||
L = T - U = \dfrac{3}{4}m\dot{s}^2 - mgs - \dfrac{1}{2}k(s-l_0)^2 | |||
</math> | </math> | ||
</center> | </center> | ||
La ecuación de Euler para <math>s</math> es | |||
<center> | <center> | ||
<math> | <math> | ||
\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{s}}\right) | |||
- \dfrac{\partial L}{\partial s} = 0 | |||
\dfrac | |||
</math> | </math> | ||
</center> | </center> | ||
Haciendo las derivadas obtenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \dfrac{3}{2}m\ddot{s} + k(s-l_0) + mg = 0 | ||
</math> | </math> | ||
</center> | </center> | ||
Podemos reordenar la ecuación | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \ddot{s} = -\dfrac{2k}{3m}s - \dfrac{2}{3}g + \dfrac{2kl_0}{3m} | ||
= | |||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
Es la ecuación de movimiento de un oscilador armónico con frecuencia angular y período | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \omega_0 = \sqrt{\dfrac{2k}{3m}}, | ||
\ | \qquad | ||
\tau = \dfrac{2\pi}{\omega_0} = 2\pi \sqrt{\dfrac{3m}{2k}} | |||
\ | |||
= | |||
\ | |||
\ | |||
= | |||
\ | |||
\ | |||
</math> | </math> | ||
</center> | </center> | ||
La | La posición de equilibrio se obtiene imponiendo <math>\ddot{s}=0</math> | ||
<center> | <center> | ||
<math> | <math> | ||
s_{eq} = l_0 - \dfrac{mg}{2k} | |||
</math> | </math> | ||
</center> | </center> | ||
== Aplicación de un par de fuerzas externo <math>\vec{\tau}=\tau_0\cos(\omega t)\,\vec{k}_1</math>== | |||
El par de fuerzas externo introduce una fuerza generalizada no conservativa en la ecuación de Euler | |||
<center> | <center> | ||
<math> | <math> | ||
\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{s}}\right) | |||
- \dfrac{\partial L}{\partial s} = Q_s^{NC} | |||
</math> | </math> | ||
</center> | </center> | ||
El lado izquierdo de la ecuación queda igual que antes. Calculamos la fuerza generalizada | |||
<center> | <center> | ||
<math> | <math> | ||
Q^{NC}_s = \vec{\tau}\cdot\dfrac{\partial\vec{\omega}_{21}}{\partial\dot{s}} | |||
= | |||
-\dfrac{\tau_0}{R}\cos(\omega t) | |||
</math> | </math> | ||
</center> | </center> | ||
La ecuación del movimiento es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \ddot{s} +\dfrac{2k}{3m}s + \dfrac{2}{3}g . \dfrac{2kl_0}{3m} = -\dfrac{2\tau_0}{3mR}\cos(\omega t) | ||
</math> | </math> | ||
</center> | </center> | ||
Es la ecuación de un oscilador forzado con un término de forzamiento dado por el par de fuerzas y de frecuencia <math>\omega</math>. La resonancia mecánica aparece cuando esta frecuencia se acerca a la frecuencia natural del oscilador calculada antes | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \omega \simeq \omega_0 = \sqrt{\dfrac{2k}{3m}} | ||
</math> | </math> | ||
</center> | </center> | ||
== | == Percusión == | ||
Ahora, sin par de fuerzas externo, se aplica una percusión en <math>B</math> de forma | |||
<center> | |||
<math> | |||
\vec{\hat{F}} = [\hat{F}_0, \hat{F}_0, 0]_{1} | |||
</math> | |||
</center> | |||
La ecuación de Lagrange percusiva es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \Delta p_{s} = \hat{Q}^{NC}_s | ||
</math> | </math> | ||
</center> | </center> | ||
El momento generalizado es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | p_s = \dfrac{\partial L}{\partial \dot{s}} = \dfrac{3}{2}m\dot{s} | ||
</math> | </math> | ||
</center> | </center> | ||
Entonces | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \Delta p_s = \dfrac{3}{2}m(\dot{s}(0^+)-\dot{s}(0^-)) = \dfrac{3}{2}ms(0^+) | ||
</math> | </math> | ||
</center> | </center> | ||
La percusión generalizada es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \hat{Q}^{NC}_s = \vec{\hat{F}}\cdot\dfrac{\partial \vec{v}^{\,B}_{21}}{\partial \dot{s}} | ||
\vec{\ | |||
</math> | </math> | ||
</center> | </center> | ||
La velocidad absoluta en <math>B</math> es | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{v}^{\,B}_{21} = \vec{v}^{\,C}_{21} + \vec{\omega}_{21}\times\overrightarrow{CB} = -\dot{s}\,\vec{\jmath}_1 | |||
</math> | </math> | ||
</center> | </center> | ||
La percusión generalizada es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \hat{Q}^{NC}_s = -\hat{F}_0 | ||
</math> | </math> | ||
</center> | </center> | ||
La velocidad generalizada justo después de la percusión es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \dot{s}(0^+) = -\dfrac{2\hat{F}_0}{3m} | ||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría:Problemas de Dinámica | [[Categoría:Problemas de mecánica analítica]] | ||
[[Categoría:Problemas de Dinámica Analítica]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | [[Categoría:Problemas de examen de Mecánica Racional]] | ||
Revisión actual - 12:45 8 nov 2023
Enunciado
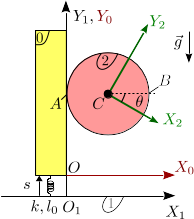
Un disco homogéneo (sólido "2") de masa y radio puede rotar alrededor de su centro , que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa puede moverse a lo largo del eje , de modo que en el punto de contacto el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un muelle de constante elástica y longitud natural . El otro extremo del muelle está anclado en un punto fijo del eje , de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura.
- ¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales.
- Calcula las energías cinética y potencial del sistema en función de sus grados de libertad.
- Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento.
- Se aplica sobre el disco un par de fuerzas externo . Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de aparece una resonancia mecánica?
- Ahora no hay par aplicado. Se aplica una percusión sobre el punto del sólido "2". En el instante de la percusión se cumple , , , . Calcula el estado del sistema inmediatamente después de la percusión.
Solución
Reducciones cinemáticas y grados de libertad
Movimiento {01}
La deslizadera realiza un movimiento de traslación vertical. Tenemos
No ponemos letras en la velocidad y aceleración pues es una traslación y son iguales en todos los puntos.
Movimiento {21}
El disco hace una rotación con su centro fijo. Tenemos
Movimiento {20}
Usamos las reglas de composición
Grados de libertad
La condición de rodadura sin deslizamiento impone una ligadura entre y
Es decir, el sistema tiene un grado de libertad. Elegiremos para describir el movimiento.
Energía cinética y potencial
La energía cinética total es la suma de la energía cinética de cada sólido
La deslizadera tiene sólo energía cinética de traslación
El disco tiene sólo energía cinética de rotación
La energía cinética total es
La deslizadera tiene energía potencial y elástica. El centro del masas del disco no cambia su altura, por lo que su energía potencial gravitatoria es constante y no afecta a la dinámica del sistema. Podemos ignorarla. Tenemos
Lagrangiana y ecuaciones de Euler
La función de Lagrange es
La ecuación de Euler para es
Haciendo las derivadas obtenemos
Podemos reordenar la ecuación
Es la ecuación de movimiento de un oscilador armónico con frecuencia angular y período
La posición de equilibrio se obtiene imponiendo
Aplicación de un par de fuerzas externo
El par de fuerzas externo introduce una fuerza generalizada no conservativa en la ecuación de Euler
El lado izquierdo de la ecuación queda igual que antes. Calculamos la fuerza generalizada
La ecuación del movimiento es
Es la ecuación de un oscilador forzado con un término de forzamiento dado por el par de fuerzas y de frecuencia . La resonancia mecánica aparece cuando esta frecuencia se acerca a la frecuencia natural del oscilador calculada antes
Percusión
Ahora, sin par de fuerzas externo, se aplica una percusión en de forma
La ecuación de Lagrange percusiva es
El momento generalizado es
Entonces
La percusión generalizada es
La velocidad absoluta en es
La percusión generalizada es
La velocidad generalizada justo después de la percusión es










![{\displaystyle {\vec {\hat {F}}}=[{\hat {F}}_{0},{\hat {F}}_{0},0]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45be34e4e576e91e7146a6c511e29b15fa8bb600)


































