Diferencia entre las páginas «Mecánica Racional (Ingeniería Civil)» y «Partícula deslizando sobre un disco (GIA)»
Sin resumen de edición |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | |||
[[Imagen:F1_GIA_masa_resbalando_sobre_disco_enunciado.png|right]] | |||
Una partícula <math>P</math>, de masa <math>m</math>, es abandonada en reposo en el punto más alto de un disco vertical de radio <math>R</math> que descansa apoyado en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determina el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo. | |||
< | |||
== Solución == | |||
Este es un ejemplo de vínculo unilateral. La condición sobre el | |||
movimiento de la partícula es que no penetre en el disco. Mientras hay | |||
contacto con el disco la fuerza de reacción se ajusta para que la | |||
partícula esté siempre fuera de él. Una vez que deja de haber | |||
contacto la partícula se mueve como si fuera libre. Por otro lado hay | |||
un vínculo bilateral que impone que el movimiento se desarrolle en el | |||
plano del dibujo. La inecuación y la ecuación que | |||
definen estos vínculos serían, escogiendo el sistema de ejes de la figura y | |||
usando coordenadas polares | |||
<center><math> | |||
(1) | |||
\rho \geq R\qquad\qquad z=0 | |||
</math></center> | |||
Esto nos deja un grado de libertad para el movimiento mientras hay | |||
contacto y dos cuando deja de haberlo. Aquí sólo nos interesa | |||
describir el movimiento mientras el contacto existe, para encontrar el | |||
ángulo para el que cesa. | |||
[[Imagen:F1_GIA_masa_resbalando_sobre_disco_a.png|right]] | |||
Mientras la partícula desliza sobre el disco, las fuerzas que actúan | |||
sobre ella son su peso y la fuerza de reacción, que es normal al disco | |||
pues suponemos que no hay rozamiento. Usando coordenadas polares | |||
tenemos | |||
<center><math> | |||
(2) | |||
\begin{array}{l} | |||
\vec{\Phi}=\Phi\,\vec{u}_{\rho}\\ \\ | |||
m\vec{g}=-mg\,\vec{\jmath}=-mg\,\mathrm{sen}\,\theta\,\vec{u}_{\rho}-mg\cos\theta\,\vec{u}_{\theta} | |||
\end{array} | |||
</math></center> | |||
Por otro lado, como vimos en un problema anterior, la aceleración es, | |||
teniendo en cuenta que <math>\rho=R</math>, | |||
<center><math> | |||
(3) | |||
\begin{array}{l} | |||
\vec{r}=R\,\vec{u}_{\rho}\\ \\ | |||
\dot{\vec{r}}=R\dot{\theta}\,\vec{u}_{\theta}\\ \\ | |||
\ddot{\vec{r}}=-R\dot{\theta}^2\vec{u}_{\rho}+R\ddot{\theta}\,\vec{u}_{\theta} | |||
\end{array} | |||
</math></center> | |||
La Segunda Ley de Newton nos da | |||
<center><math> | |||
(4) | |||
m\ddot{\vec{r}}=m\vec{g}+\vec{\Phi} | |||
\Rightarrow | |||
\left\{ | |||
\begin{array}{l} | |||
-mR\dot{\theta}^2=-mg\,\mathrm{sen}\,\theta+\Phi\\ \\ | |||
mR\ddot{\theta}=-mg\cos\theta | |||
\end{array} | |||
\right. | |||
\Rightarrow | |||
\left\{ | |||
\begin{array}{l} | |||
\Phi=mg\,\mathrm{sen}\,\theta-mR\dot{\theta}^2\\ \\ | |||
\ddot{\theta}=-(g/R)\cos\theta | |||
\end{array} | |||
\right. | |||
</math></center> | |||
Resolviendo la segunda ecuación con las condiciones iniciales | |||
adecuadas tendríamos el movimiento descrito. Pero aquí no podemos | |||
utilizar la aproximación de ángulo pequeño del problema con el aro, | |||
así que no podemos resolver el problema de manera | |||
sencilla. Afortunadamente no es necesario hacerlo para encontrar el | |||
ángulo de separación. | |||
Vamos a examinar la evolución del módulo de la fuerza de reacción, | |||
<math>\Phi</math>. Cuando la masa está arriba, en reposo (<math>v=0</math>), se tiene | |||
<center><math> | |||
(5) | |||
\left. | |||
\begin{array}{l} \theta=\pi/2\\ \dot{\theta}=0\end{array}\right\} | |||
< | \quad\Rightarrow\quad \Phi=mg | ||
< | </math></center> | ||
En este instante la fuerza de reacción equilibra el peso de la | |||
masa. Cuando empieza a deslizar, <math>\,\mathrm{sen}\,\theta</math> disminuye y | |||
<math>\dot{\theta}</math> aumenta. Por tanto <math>\Phi</math> va disminuyendo. La fuerza de | |||
reacción se va ajustando para obligar a que la partícula no penetre en | |||
el disco. La masa se separa cuando se cumple <math>\Phi=0</math>. | |||
Necesitamos <math>\dot{\theta}</math>, pero para calcularla no hace falta | |||
resolver el problema completo. <math>\dot{\theta}</math> está relacionada con el | |||
módulo de la velocidad, es decir, con la energía cinética. Entonces, | |||
vamos a aplicar la conservación de energía mecánica para | |||
calcularla. La energía mecánica en el instante inicial es únicamente | |||
potencial gravitatoria, pues la partícula parte del reposo. Al ir cayendo, su | |||
energía potencial disminuye y su energía cinética aumenta, pero su | |||
suma es siempre constante. Tenemos | |||
<center><math> | |||
(6) | |||
\begin{array}{l} | |||
E=U(y=R)=mgR=U(y)+T(y) = mgy+\frac{1}{2}mv^2 \Rightarrow\\ \\ | |||
v(y) = \sqrt{2g(R-y)} | |||
\end{array} | |||
</math></center> | |||
[[Imagen:F1_GIA_masa_resbalando_sobre_disco_b.png|right]] | |||
Hemos escogido como referencia de energía potencial <math>\left.U\right|_{y=0} = 0</math>. | |||
De (3) tenemos | |||
<center><math> | |||
(7) | |||
v = |\dot{\vec{r}}| = R\dot{\theta} \Rightarrow | |||
\dot{\theta}(y)=\frac{v(y)}{R} = \frac{\sqrt{2g(R-y)}}{R} | |||
</math></center> | |||
Podemos ahora expresar <math>\Phi</math> en función de <math>\theta</math> | |||
<center><math> | |||
(8) | |||
\begin{array}{ll} | |||
\Phi = mg\,\mathrm{sen}\,\theta-\frac{\displaystyle 2mg(R-y)}{\displaystyle R}&=\\ &\\ | |||
mg ( \,\mathrm{sen}\,\theta-2+2\frac{\displaystyle y}{\displaystyle R})&=mg ( 3\,\mathrm{sen}\,\theta-2) | |||
\end{array} | |||
</math></center> | |||
Hemos usado que la variable <math>y</math> es | |||
<center><math> | |||
(9) | |||
y=R\,\mathrm{sen}\,\theta | |||
</math></center> | |||
Imponiendo <math>\Phi=0</math> obtenemos el ángulo buscado | |||
<center><math> | |||
(10) | |||
\Phi=0\Longrightarrow \,\mathrm{sen}\,\theta_s=2/3\Longrightarrow | |||
\theta_s=0.730\,\mathrm{rad}=41.8^o | |||
</math></center> | |||
Una vez que se ha interrumpido el contacto, la partícula describe una | |||
trayectoria parabólica, pues se mueve libremente en el seno del campo gravitatorio. Podríamos determinar la velocidad inicial y calcular la | |||
trayectoria, pero sólo nos piden la velocidad, <math>v_f</math> cuando llega al | |||
suelo, es decir, para <math>y=-R</math>. Aplicando la conservación de energía | |||
mecánica, tenemos | |||
<center><math> | |||
(11) | |||
E = mgR = U(-R)+T(-R)=-mgR+\frac{1}{2}mv_f^2\Longrightarrow | |||
v_f=2\sqrt{gR} | |||
</math></center> | |||
[[Categoría:Problemas de Dinámica de la partícula]] | |||
[[Categoría:Problemas de Cinética de la partícula]] | |||
[[Categoría:Dinámica del punto material|1]] | |||
[[Categoría:Física I (G.I.A.)]] | |||
[[Categoría:Física I (G.I.T.I.)]] | |||
Revisión actual - 14:24 31 oct 2023
Enunciado
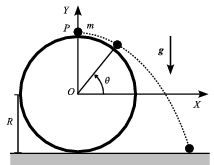
Una partícula , de masa , es abandonada en reposo en el punto más alto de un disco vertical de radio que descansa apoyado en el suelo. Debido a una ligera perturbación, la partícula comienza a deslizar bajo la acción de la gravedad. Suponiendo que no hay rozamiento, determina el punto en el que la partícula pierde contacto con el disco, así como la velocidad con la que impacta contra el suelo.
Solución
Este es un ejemplo de vínculo unilateral. La condición sobre el movimiento de la partícula es que no penetre en el disco. Mientras hay contacto con el disco la fuerza de reacción se ajusta para que la partícula esté siempre fuera de él. Una vez que deja de haber contacto la partícula se mueve como si fuera libre. Por otro lado hay un vínculo bilateral que impone que el movimiento se desarrolle en el plano del dibujo. La inecuación y la ecuación que definen estos vínculos serían, escogiendo el sistema de ejes de la figura y usando coordenadas polares
Esto nos deja un grado de libertad para el movimiento mientras hay contacto y dos cuando deja de haberlo. Aquí sólo nos interesa describir el movimiento mientras el contacto existe, para encontrar el ángulo para el que cesa.
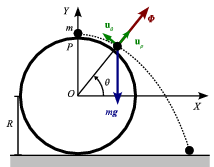
Mientras la partícula desliza sobre el disco, las fuerzas que actúan sobre ella son su peso y la fuerza de reacción, que es normal al disco pues suponemos que no hay rozamiento. Usando coordenadas polares tenemos
Por otro lado, como vimos en un problema anterior, la aceleración es, teniendo en cuenta que ,
La Segunda Ley de Newton nos da
Resolviendo la segunda ecuación con las condiciones iniciales adecuadas tendríamos el movimiento descrito. Pero aquí no podemos utilizar la aproximación de ángulo pequeño del problema con el aro, así que no podemos resolver el problema de manera sencilla. Afortunadamente no es necesario hacerlo para encontrar el ángulo de separación.
Vamos a examinar la evolución del módulo de la fuerza de reacción, . Cuando la masa está arriba, en reposo (), se tiene
En este instante la fuerza de reacción equilibra el peso de la masa. Cuando empieza a deslizar, disminuye y aumenta. Por tanto va disminuyendo. La fuerza de reacción se va ajustando para obligar a que la partícula no penetre en el disco. La masa se separa cuando se cumple .
Necesitamos , pero para calcularla no hace falta resolver el problema completo. está relacionada con el módulo de la velocidad, es decir, con la energía cinética. Entonces, vamos a aplicar la conservación de energía mecánica para calcularla. La energía mecánica en el instante inicial es únicamente potencial gravitatoria, pues la partícula parte del reposo. Al ir cayendo, su energía potencial disminuye y su energía cinética aumenta, pero su suma es siempre constante. Tenemos
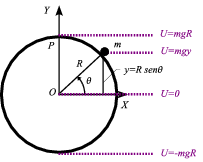
Hemos escogido como referencia de energía potencial . De (3) tenemos
Podemos ahora expresar en función de
Hemos usado que la variable es
Imponiendo obtenemos el ángulo buscado
Una vez que se ha interrumpido el contacto, la partícula describe una trayectoria parabólica, pues se mueve libremente en el seno del campo gravitatorio. Podríamos determinar la velocidad inicial y calcular la trayectoria, pero sólo nos piden la velocidad, cuando llega al suelo, es decir, para . Aplicando la conservación de energía mecánica, tenemos
























