Línea 1:
Línea 1: ==Enunciado==
==Enunciado==
En un hipotético sólido rígido, consideramos los puntos
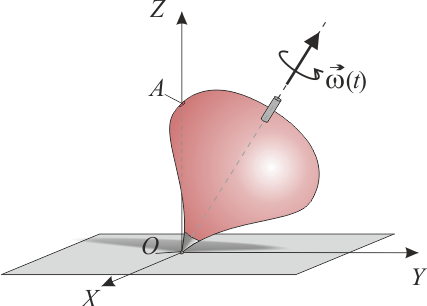
[[Archivo:el_trompo_1.gif|right]]El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando , manteniéndose fijo el punto de apoyo. Supongamos el caso particular
<center><math>\overrightarrow{OA}=\vec{\imath}\qquad\overrightarrow{OB}=\vec{\jmath}\qquad\overrightarrow{OC}=\vec{k}</math></center>
<center><math>\vec{v}^ {\, O }(t) =\vec{0} \qquad \qquad\vec {\omega }(t) =3\cos(t) \vec{\imath }+3 \,\mathrm{sen}(t) \vec {\jmath }+4 \vec{k}</math></center>
y analizamos los casos correspondientes a las siguientes velocidades para los
Consideremos el punto <math>\overrightarrow{OA}=\vec{k}</math>
tres puntos:
{| class="bordeado"
# Determine la velocidad de este punto en cada instante.
|-
# Determine la aceleración de A en todo instante.
! Caso
# Halle, para cada instante, las componentes intrínsecas de la aceleración y el radio de curvatura en el mismo punto.
! <math>\vec{v}^A</math>
! <math>\vec{v}^B</math>
! <math>\vec{v}^C</math>
|-
! I
| <math>2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>
| <math>2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>
| <math>2\vec{k}</math>
|-
! II
| <math>2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>
| <math>3\vec{\imath}+2\vec{\jmath}</math>
| <math>2\vec{\imath}+4\vec{\jmath} + 2\vec{k}</math>
|-
! III
| <math>2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>
| <math>2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>
| <math>2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>
|-
! IV
| <math>2\vec{\imath}+3\vec{\jmath}</math>
| <math>\vec{\imath}+2\vec{\jmath}-\vec{k}</math>
| <math>4\vec{\imath}+4\vec{\jmath}+2\vec{k}</math>
|-
! V
| <math>2\vec{\imath}+\vec{k}</math>
| <math>4\vec{\imath}+2\vec{\jmath}+3\vec{k}</math>
| <math>3\vec{\imath}+\vec{\jmath}+2\vec{k}</math>
|-
! VI
| <math>2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>
| <math>3\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>
| <math>-\vec{\imath}+\vec{\jmath}+2\vec{k}</math>
|}
Todas las cantidades están expresadas en las unidades del SI.
Todas las cantidades están expresadas en las unidades del SI.
Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.
==Solución==
===Velocidad instantánea===
Por tratarse de una rotación pura
==Introducción==
<center><math>\vec{v}^A = \overbrace{\vec{v}^O}^{ =\vec{0}} + \vec{\omega}\times\overrightarrow{OA} =
Para identificar los diferentes estados de movimiento, conocidas las velocidades de tres puntos no alineados, podemos seguir el siguiente esquema:
\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k}\\ 3\cos(t) & 3\ ,\mathrm{sen}(t) & 4 \\ 0 & 0 & 1\end{matrix}\right|=3\ ,\mathrm{sen}(t)\vec{\imath}-3\cos(t)\vec{\jmath}</math></center>
<center>[[Archivo:flujo-solido-2.jpg]]</center>
===Aceleración instantánea===
El campo de aceleraciones tiene la expresión general
==Caso I==
<center><math>\vec{a}^A = \vec{a}^O + \vec{\alpha}\times\overrightarrow{OA}+\vec{\omega}\times(\vec{\omega}\times\overrightarrow{OA}) =\vec{a}^O + \vec{\alpha}\times\overrightarrow{OA}+\vec{\omega}\times(\vec{v}^A-\vec{v}^O)</math></center>
Tenemos las velocidades
<center><math>\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{k}</math></center>
En este caso la velocidad y la aceleración de O son nulas, por estar permanentemente en reposo, mientras que la aceleración angular vale
Comprobamos primero si se trata de un posible movimiento rígido, chequeando la condición de equiproyectividad para cada par de puntos
<center><math>\vec{v}^O=\vec{0}</math>{{qquad}}{{qquad}}<math>\vec{a}^O = \frac{\mathrm{d}\vec{v}^O}{\mathrm{d}t}=\vec{0}</math>{{qquad}}{{qquad}}<math>\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}=-3\ ,\mathrm{sen}(t)\vec{\imath}+3\cos(t)\vec{\jmath}</math></center>
;Partículas A y B:
Sustituyendo
<center><math>\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 0 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 0 \end{matrix}\right.</math></center>
;Partículas A y C:
<center><math>\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 2 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 2 \end{matrix}\right.</math></center>
;Partículas B y C:
<center><math>\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 2 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 2 \end{matrix}\right.</math></center>
Se verifica en los tres casos, por lo que se trata de un movimiento posible para un sólido rígido.
A continuación, comprobamos si las tres velocidades son iguales. No lo son. Por tanto, no puede tratarse de una traslación o un estado de reposo.
Vemos ahora si las velocidades son coplanarias
<center><math>\vec{v}^A\cdot(\vec{v}^B\times\vec{v}^C)=\left|\begin{matrix}2 & 2 & 4 \\ 2 & 2 & 4 \\ 0 & 0 & 2\end{matrix}\right|=0</math></center>
Al haber dos velocidades iguales, necesariamente los tres vectores son coplanarios. Necesitamos hallar entonces la dirección de la velocidad angular. Esto es fácil; al haber dos velocidades iguales, la velocidad angular va en la dirección de la recta que pasa por esos dos puntos. En este caso
<center><math>\vec{\omega} = \lambda\overrightarrow{AB}=\lambda(-\vec{\imath}+\vec{\jmath})</math></center>
y comprobamos ahora si alguna de las velocidades es perpendicular a esta dirección. No necesitamos volver a calcular nada, ya que lo hicimos previamente:
<center><math>\vec{v}^A\cdot\overrightarrow{AB}=0</math></center>
Por tanto se trata de un movimiento de '''rotación pura'''.
==Caso II==
Tenemos las velocidades
<center><math>\vec{v}^A=2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=3\vec{\imath}+2\vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{\imath}+4\vec{\jmath} + 2\vec{k}</math></center>
Comprobamos la equiproyectividad
;Partículas A y B:
<center><math>\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (3\vec{\imath}+2\vec{\jmath})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \end{matrix}\right.</math></center>
;Partículas A y C:
<center><math>\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 0 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (2\vec{\imath}+4\vec{\jmath} + 2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 0 \end{matrix}\right.</math></center>
;Partículas B y C:
<center><math>\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (3\vec{\imath}+2\vec{\jmath})\cdot(-\vec{\jmath}+\vec{k}) & = & -2 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (2\vec{\imath}+4\vec{\jmath} + 2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & -2 \end{matrix}\right.</math></center>
De nuevo se verifica en los tres casos, por lo que se trata de un movimiento posible.
Puesto que las tres velocidades no son iguales, no puede tratarse de una traslación o un estado de reposo.
Verificamos entonces si las velocidades son coplanarias:
<center><math>\vec{v}^A\cdot(\vec{v}^B\times\vec{v}^C) = \left|\begin{matrix} 2 & 1 & 2 \\ 3 & 2 & 0 \\ 2 & 4 & 2 \end{matrix}\right| = 18\neq 0</math></center>
Por no ser nulo, se trata de un movimiento '''helicoidal'''.
==Caso III==
El tercer caso
<center><math>\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{\imath}+2\vec{\jmath} + 2\vec{k}</math></center>
puede clasificarse por simple inspección. Puesto que las tres velocidades son iguales, y no nulas, se trata de un movimiento de '''traslación'''.
==Caso IV==
En este caso, las velocidades valen
<center><math>\vec{v}^A=2\vec{\imath}+3\vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=\vec{\imath}+2\vec{\jmath}-\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=4\vec{\imath}+4\vec{\jmath}+2\vec{k}</math></center>
Examinamos la condición de rigidez
;Partículas A y B:
<center><math>\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+3\vec{\jmath})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 1 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (\vec{\imath}+2\vec{\jmath}-\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 1 \end{matrix}\right.</math></center>
;Partículas A y C:
<center><math>\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+3\vec{\jmath})\cdot(-\vec{\imath}+\vec{k}) & = & -2 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (4\vec{\imath}+4\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & -2 \end{matrix}\right.</math></center>
;Partículas B y C:
<center><math>\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (\vec{\imath}+2\vec{\jmath}-\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & -3 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (4\vec{\imath}+4\vec{\jmath}+2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & -2 \end{matrix}\right.</math></center>
Puesto que no se cumple la condición de equiproyectividad, este caso es '''imposible''' como movimiento de un sólido rígido.
==Caso V==
En este caso, tenemos las velocidades
<center><math>\vec{v}^A=2\vec{\imath}+\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=4\vec{\imath}+2\vec{\jmath}+3\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=3\vec{\imath}+\vec{\jmath}+2\vec{k}</math></center>
Examinamos la equiproyectividad
;Partículas A y B:
<center><math>\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -2 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (4\vec{\imath}+2\vec{\jmath}+3\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -2 \end{matrix}\right.</math></center>
;Partículas A y C:
<center><math>\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & -1\\ \vec{v}^C\cdot\overrightarrow{AC} & = & (3\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & -1 \end{matrix}\right.</math></center>
;Partículas B y C:
<center><math>\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (4\vec{\imath}+2\vec{\jmath}+3\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 1 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (3\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 1 \end{matrix}\right.</math></center>
De nuevo se verifica en los tres casos, por lo que se trata de un movimiento posible.
Las tres velocidades no son iguales, por lo que no puede tratarse de una traslación o un estado de reposo.
Verificamos entonces si las velocidades son coplanarias:
<center><math>\vec{v}^A\cdot(\vec{v}^B\times\vec{v}^C) = \left|\begin{matrix} 2 & 0 & 1 \\ 4 & 2 & 3 \\ 3 & 1 & 2 \end{matrix}\right| = 0</math></center>
Puesto que es nulo, debemos ahora determinar la dirección de la velocidad angular. Para ello suponemos una velocidad angular de la forma
<center><math>\vec{\omega} = \omega_x\vec{\imath}+\omega_y\vec{\jmath}+\omega_\vec{k}</math></center>
y sustituimos en las relaciones
<center><math>\vec{v}^B-\vec{v}^A = \vec{\omega}\times\overrightarrow{AB}</math>{{qquad}}{{qquad}}<math>\vec{v}^C-\vec{v}^A = \vec{\omega}\times\overrightarrow{AC}</math></center>
Para el par A y B queda
<center><math>
2\vec{\imath}+2\vec{\jmath}+2\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\
\omega_x & \omega_y & \omega_z\\ -1 & 1 & 0 \end{matrix}\right| = -\omega_z\vec{\imath} -\omega_z \vec{\jmath}+(\omega_x +\omega_y)\vec{k}</math></center>
de donde
<center><math>\omega_x+\omega_y = 2\qquad\qquad\omega_z = -2</math></center>
Repitiendo para A y C
<center><math>
<center><math>
\vec{\imath}+\vec{\jmath}+\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\
\vec{a}^A = \vec{\alpha}\times\overrightarrow{OA }+\vec{\omega }\times \vec{v }^A = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k}\\ -3\, \mathrm{sen}(t) & 3 \cos(t) & 0 \\ 0 & 0 & 1\end{matrix}\right| + \left|\begin{matrix} \vec{\imath} & \vec{\jmath} & \vec{k}\\ 3\cos(t) & 3\,\mathrm{sen}(t) & 4 \\ 3\,\mathrm{sen}(t) & -3\cos (t) & 0 \end{matrix}\right|= 15\cos(t)\vec{\imath} +15\, \mathrm{sen}(t )\vec{\jmath}-9 \vec{k}</math></center>
\omega_x & \omega_y & \omega_z\\ -1 & 0 & 1 \end{matrix}\right| = \omega_y\vec{\imath} -(\omega_x+\omega_z) \vec{\jmath}+\omega_y\vec{k}</math></center>
de donde
<center><math>\omega_x+\omega_z = -1\qquad\qquad\omega_y = 1</math></center>
Puede comprobarse de manera inmediata que
lo que nos da la velocidad angular
<center><math>\vec{a}^A\neq \frac{\partial\vec{v}^A}{\partial t}=3\cos(t)\vec{\imath}+3\,\mathrm{sen}(t)\vec{\jmath}</math></center>
<center><math>\vec{\omega}=\vec{\imath}+\vec{\jmath}-2\vec{k}</math></center>
¿Por qué pasa esto si sabemos que la aceleración de una partícula es la derivada de su velocidad respecto al tiempo? La razón es que estamos considerando ''diferentes partículas''. Cuando hallamos la velocidad del punto A en un instante dado, estamos calculando la velocidad de la partícula material que ''en ese momento ocupa el punto A''. Pero esa partícula se está moviendo, por lo que un instante después se habrá desplazado a otro sitio, y ''otra partícula habrá ocupado su lugar''. Cuando calculamos la cantidad
Comprobamos ahora si cualquiera de las velocidades es perpendicular a esta velocidad angular
<center><math>\frac{\partial\vec{v}^A}{\partial t} = \lim_{\Delta t\to 0}\frac{\vec{v}^A(t+\Delta t)-\vec{v}^A(t)}{\Delta t}</math></center>
<center><math>\vec{v}^A\cdot\vec{\omega} = (2\vec{\imath}+\vec{k})\cdot(\vec{\imath}+\vec{\jmath}-2\vec{k})= 0</math></center>
estamos restando las velocidades de partículas materiales diferentes (la que se halla en A en <math >t+\Delta t </ math> y la que se halla en A en el instante <math>t </math >) y por tanto el resultado no tiene por qué coincidir con la aceleración de ninguna de ellas.
Puesto que la velocidad lineal es perpendicular a la velocidad angular, la velocidad de deslizamiento es nula y el movimiento es de '''rotación pura'''.
El cálculo según la expresión del campo de aceleraciones, en cambio , sí nos da el valor correcto de la aceleración de la partícula que se halla en A en el instante <math>t</math> .
==Caso VI==
===Componentes intrínsecas= ==
Por último, tenemos las velocidades,
Hemos obtenido que , para cada instante ,
<center><math>\vec{v}^A=2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=3\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=-\vec{\imath}+\vec{\jmath}+2\vec{k}</math></center>
<center><math>\vec{v}^A = 3 \, \mathrm {sen }(t) \vec{\imath }- 3\cos(t) \vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{a }^A = 15\cos(t) \vec{\imath}+15\,\mathrm{sen}(t) \vec{\jmath}-9 \vec{k}</math></center>
Testeamos la condición de rigidez
Una vez que tenemos los vectores velocidad aceleración podemos hallar las componentes intrínsecas de la aceleración.
;Partículas A y B:
;Aceleración tangencial : Proyectando sobre la velocidad
<center><math>\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (3\vec{\imath}+2\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \end{matrix}\right.</math></center>
<center><math>\vec {a }^A_t = \frac {( \vec{a }^A \cdot \vec{v}^A) \vec{v }^A }{(v^A )^2 } = \vec{0 }</math></center>
;Partículas A y C:
;Aceleración normal : Puesto que la aceleración tangencial es nula, toda la aceleración es normal
<center><math>\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 0 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (-\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 3 \end{matrix}\right.</math></center>
<center><math>\vec {a }^A_n = \vec{a }^A = 15 \cos (t) \vec{\imath}+15 \, \mathrm {sen }(t )\vec{\jmath}-9 \vec{k}</math></center>
No necesitamos continuar. Una vez que se viola la equiproyectividad podemos afirmar que se trata de un movimiento '''imposible''' para un sólido rígido.
;Radio de curvatura:Es inmediato conocida la aceleración normal y la celeridad
==Resumen==
<center><math>R_{\kappa} = \frac{(v^A)^2}{a^A_n} = \frac{3}{\sqrt{34}} </math></center>
Reuniendo los resultados de los seis casos queda
<center>
{| class="bordeado"
|-
! Caso
! Estado
|-
! I
| Rotación
|-
! II
| Helicoidal
|-
! III
| Traslación
|-
! IV
| Imposible
|-
! V
| Rotación
|-
! VI
| Imposible
|}
</center>
[[Categoría:Problemas de Cinemática del Sólido Rígido (GITI)]]
[[Categoría:Problemas de Cinemática del Sólido Rígido (GITI)]]
Enunciado El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular
v
→
O
(
t
)
=
0
→
ω
→
(
t
)
=
3
cos
(
t
)
ı
→
+
3
s
e
n
(
t
)
ȷ
→
+
4
k
→
{\displaystyle {\vec {v}}^{\,O}(t)={\vec {0}}\qquad \qquad {\vec {\omega }}(t)=3\cos(t){\vec {\imath }}+3\,\mathrm {sen} (t){\vec {\jmath }}+4{\vec {k}}}
Consideremos el punto
O
A
→
=
k
→
{\displaystyle {\overrightarrow {OA}}={\vec {k}}}
Determine la velocidad de este punto en cada instante.
Determine la aceleración de A en todo instante.
Halle, para cada instante, las componentes intrínsecas de la aceleración y el radio de curvatura en el mismo punto. Todas las cantidades están expresadas en las unidades del SI.
Solución Velocidad instantánea Por tratarse de una rotación pura
v
→
A
=
v
→
O
⏞
=
0
→
+
ω
→
×
O
A
→
=
|
ı
→
ȷ
→
k
→
3
cos
(
t
)
3
s
e
n
(
t
)
4
0
0
1
|
=
3
s
e
n
(
t
)
ı
→
−
3
cos
(
t
)
ȷ
→
{\displaystyle {\vec {v}}^{A}=\overbrace {{\vec {v}}^{O}} ^{={\vec {0}}}+{\vec {\omega }}\times {\overrightarrow {OA}}=\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\3\cos(t)&3\,\mathrm {sen} (t)&4\\0&0&1\end{matrix}}\right|=3\,\mathrm {sen} (t){\vec {\imath }}-3\cos(t){\vec {\jmath }}}
Aceleración instantánea El campo de aceleraciones tiene la expresión general
a
→
A
=
a
→
O
+
α
→
×
O
A
→
+
ω
→
×
(
ω
→
×
O
A
→
)
=
a
→
O
+
α
→
×
O
A
→
+
ω
→
×
(
v
→
A
−
v
→
O
)
{\displaystyle {\vec {a}}^{A}={\vec {a}}^{O}+{\vec {\alpha }}\times {\overrightarrow {OA}}+{\vec {\omega }}\times ({\vec {\omega }}\times {\overrightarrow {OA}})={\vec {a}}^{O}+{\vec {\alpha }}\times {\overrightarrow {OA}}+{\vec {\omega }}\times ({\vec {v}}^{A}-{\vec {v}}^{O})}
En este caso la velocidad y la aceleración de O son nulas, por estar permanentemente en reposo, mientras que la aceleración angular vale
v
→
O
=
0
→
{\displaystyle {\vec {v}}^{O}={\vec {0}}}
a
→
O
=
d
v
→
O
d
t
=
0
→
{\displaystyle {\vec {a}}^{O}={\frac {\mathrm {d} {\vec {v}}^{O}}{\mathrm {d} t}}={\vec {0}}}
α
→
=
d
ω
→
d
t
=
−
3
s
e
n
(
t
)
ı
→
+
3
cos
(
t
)
ȷ
→
{\displaystyle {\vec {\alpha }}={\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}=-3\,\mathrm {sen} (t){\vec {\imath }}+3\cos(t){\vec {\jmath }}}
Sustituyendo
a
→
A
=
α
→
×
O
A
→
+
ω
→
×
v
→
A
=
|
ı
→
ȷ
→
k
→
−
3
s
e
n
(
t
)
3
cos
(
t
)
0
0
0
1
|
+
|
ı
→
ȷ
→
k
→
3
cos
(
t
)
3
s
e
n
(
t
)
4
3
s
e
n
(
t
)
−
3
cos
(
t
)
0
|
=
15
cos
(
t
)
ı
→
+
15
s
e
n
(
t
)
ȷ
→
−
9
k
→
{\displaystyle {\vec {a}}^{A}={\vec {\alpha }}\times {\overrightarrow {OA}}+{\vec {\omega }}\times {\vec {v}}^{A}=\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\-3\,\mathrm {sen} (t)&3\cos(t)&0\\0&0&1\end{matrix}}\right|+\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\3\cos(t)&3\,\mathrm {sen} (t)&4\\3\,\mathrm {sen} (t)&-3\cos(t)&0\end{matrix}}\right|=15\cos(t){\vec {\imath }}+15\,\mathrm {sen} (t){\vec {\jmath }}-9{\vec {k}}}
Puede comprobarse de manera inmediata que
a
→
A
≠
∂
v
→
A
∂
t
=
3
cos
(
t
)
ı
→
+
3
s
e
n
(
t
)
ȷ
→
{\displaystyle {\vec {a}}^{A}\neq {\frac {\partial {\vec {v}}^{A}}{\partial t}}=3\cos(t){\vec {\imath }}+3\,\mathrm {sen} (t){\vec {\jmath }}}
¿Por qué pasa esto si sabemos que la aceleración de una partícula es la derivada de su velocidad respecto al tiempo? La razón es que estamos considerando diferentes partículas . Cuando hallamos la velocidad del punto A en un instante dado, estamos calculando la velocidad de la partícula material que en ese momento ocupa el punto A . Pero esa partícula se está moviendo, por lo que un instante después se habrá desplazado a otro sitio, y otra partícula habrá ocupado su lugar . Cuando calculamos la cantidad
∂
v
→
A
∂
t
=
lim
Δ
t
→
0
v
→
A
(
t
+
Δ
t
)
−
v
→
A
(
t
)
Δ
t
{\displaystyle {\frac {\partial {\vec {v}}^{A}}{\partial t}}=\lim _{\Delta t\to 0}{\frac {{\vec {v}}^{A}(t+\Delta t)-{\vec {v}}^{A}(t)}{\Delta t}}}
estamos restando las velocidades de partículas materiales diferentes (la que se halla en A en
t
+
Δ
t
{\displaystyle t+\Delta t}
t
{\displaystyle t}
El cálculo según la expresión del campo de aceleraciones, en cambio, sí nos da el valor correcto de la aceleración de la partícula que se halla en A en el instante
t
{\displaystyle t}
Componentes intrínsecas Hemos obtenido que, para cada instante,
v
→
A
=
3
s
e
n
(
t
)
ı
→
−
3
cos
(
t
)
ȷ
→
{\displaystyle {\vec {v}}^{A}=3\,\mathrm {sen} (t){\vec {\imath }}-3\cos(t){\vec {\jmath }}}
a
→
A
=
15
cos
(
t
)
ı
→
+
15
s
e
n
(
t
)
ȷ
→
−
9
k
→
{\displaystyle {\vec {a}}^{A}=15\cos(t){\vec {\imath }}+15\,\mathrm {sen} (t){\vec {\jmath }}-9{\vec {k}}}
Una vez que tenemos los vectores velocidad aceleración podemos hallar las componentes intrínsecas de la aceleración.
Aceleración tangencial
Proyectando sobre la velocidad
a
→
t
A
=
(
a
→
A
⋅
v
→
A
)
v
→
A
(
v
A
)
2
=
0
→
{\displaystyle {\vec {a}}_{t}^{A}={\frac {({\vec {a}}^{A}\cdot {\vec {v}}^{A}){\vec {v}}^{A}}{(v^{A})^{2}}}={\vec {0}}}
Aceleración normal
Puesto que la aceleración tangencial es nula, toda la aceleración es normal
a
→
n
A
=
a
→
A
=
15
cos
(
t
)
ı
→
+
15
s
e
n
(
t
)
ȷ
→
−
9
k
→
{\displaystyle {\vec {a}}_{n}^{A}={\vec {a}}^{A}=15\cos(t){\vec {\imath }}+15\,\mathrm {sen} (t){\vec {\jmath }}-9{\vec {k}}}
Radio de curvatura
Es inmediato conocida la aceleración normal y la celeridad
R
κ
=
(
v
A
)
2
a
n
A
=
3
34
{\displaystyle R_{\kappa }={\frac {(v^{A})^{2}}{a_{n}^{A}}}={\frac {3}{\sqrt {34}}}}