Enunciado
![]() A partir del resultado del problema “Campo de un segmento”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea .
A partir del resultado del problema “Campo de un segmento”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea .
Este campo puede también hallarse mediante la ley de Gauss. ¿Cómo se llega en ese caso al resultado?
Por integración directa
Podemos calcular el campo de un hilo infinito a partir del de un segmento. Según se ve en el problema ***, el resultado es
siendo α el “ángulo de elevación” del extremo del segmento.
Si consideramos el límite en que la longitud de éste se hace infinita, en términos del ángulo de elevación equivale a hacer
Esta expresión está particularizada para el caso de que el punto donde medimos el campo esté situado sobre el eje OX. La generalización a un punto arbitrio es inmediata.
Para un punto cualquiera, sustituimos x por la distancia al eje OZ (o, aun más en general, la línea donde se halla el hilo de carga). Empleando coordenadas cilíndricas, equivale sustituir por .
Además debemos dar la dirección del campo. En el caso del eje OX, es el unitario en el sentido de x creciente, esto es, el que se aleja en línea recta del eje OX. La generalización a cualquier punto consiste en sustituir por el unitario radial .
Por tanto, la expresión del campo creado por un hilo cargado uniformemente es, en cualquier punto del espacio,
Podemos expresar este resultado en la base cartesiana como
Por la ley de Gauss
La simetría traslacional es la que se tiene cuando el sistema no cambia al realizar un desplazamiento cualquiera en una cierta dirección (típicamente de forma paralela al eje Z, que suele tomarse como eje de simetría).
El ejemplo más simple es el de un hilo rectilíneo infinitamente largo, dotado de una densidad lineal uniforme de carga, . Este modelo sirve para aproximar el campo eléctrico debido a un cable como los de los tendidos de alta tensión.
Si situamos el eje OZ sobre el hilo, la simetría implica que el campo no depende de la coordenada z.
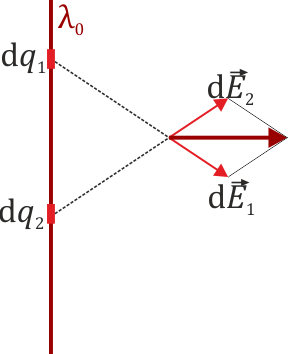
Por otro lado, para cualquier punto P del espacio, el campo debido a un elemento del hilo se suma con el de otro elemento situado simétricamente, resultando un campo perpendicular al segmento. Como además hay simetría de revolución, este campo solo puede ser radial.
Empleando coordenadas cilíndricas
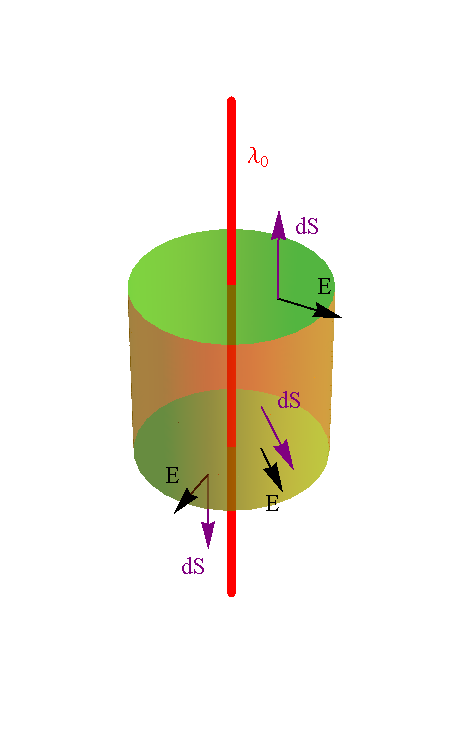
Si ahora aplicamos la ley de Gauss a una superficie cilíndrica de radio y altura concéntrica con el hilo solo hay flujo de campo a través de la cara lateral, siendo su valor
Este flujo es igual a la carga encerrada por el cilindro, dividida por la permitividad del vacío
Igualamos y despejamos y queda el campo
Este campo es radial y hacia afuera (si la densidad de carga es positiva) y decae con la distancia al hilo como la inversa de ésta (no como la inversa del cuadrado).
Podemos escribirlo en cartesianas observando que
Si tenemos más de un hilo, el campo total puede hallarse aplicando el principio de superposición.
















