Barra con extremos sobre los ejes

Dos partículas, y , de masa , están unidas por una barra rígida de longitud y masa despreciable. La partícula se mueve sobre el eje con velocidad uniforme , mientras que la partícula está obligada a moverse sobre el eje . Si en el instante la partícula se encontraba en el punto
- Encuentra la posición, velocidad y aceleración de la partícula en función de y del tiempo.
- ¿Cuál es el vector de posición y la velocidad del punto medio de la barra () en función de y ?
- Describe la curva que corresponde a la trayectoria del punto medio de la barra.
- ¿Que tipo de movimiento describe el punto medio de la barra? Razona tu respuesta.
Triángulo con muelle y rozamiento
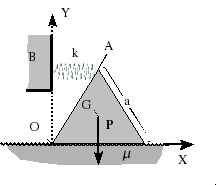
Se tiene un triángulo equilátero homogéneo de peso y lado . El peso está aplicado en el baricentro del triángulo, . El triángulo apoya uno de sus lados en una superficie rugosa, con coeficiente de rozamiento . El vértice está unido a la pared con un muelle de constante elástica y longitud natural nula. El muelle se mantiene siempre horizontal, como se indica en la figura
- Dibuja el diagrama de sólido libre del triángulo.
- Encuentra las fuerzas que actúan sobre el triángulo en situación de equilibrio mecánico.
- ¿Que condición debe cumplir para que el equilibrio se rompa por deslizamiento y no por vuelco?















