Primera Convocatoria Ordinaria 2012/13 (G.I.C.)

Masa sobre un plano inclinado conectado a un muelle y otra masa

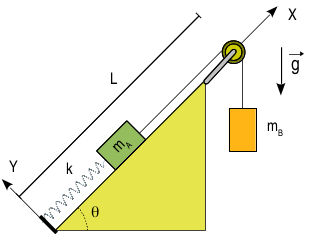
En el sistema de la figura, la masa $m_{A}$ desliza sin rozamiento sobre el plano inclinado. El muelle tiene constante elástica $k$ y longitud natural nula. La longitud de la cuerda es $l=L$. La cuerda se supone que tiene masa nula y que siempre se mantiene tensa. La masa $m_{B}$ se mueve de modo que la cuerda se mantiene siempre vertical. La cuña se supone estática en todo el problema.

1. Dibuja el diagrama de cuerpo libre de las dos masas.
2. Determina la posición $x_{eq}$ de la masa $m_{A}$ cuando el sistema está en equilibrio.
3. La masa $m_{A}$ se separa de su posición de equilibrio y se suelta. Escribe la ecuación de movimiento de la masa $m_{A}$. Demuestra que realiza un movimiento armónico simple y encuentra su período.
4. Suponiendo que el origen de energía potencial se sitúa en la base de la cuña, ¿cuánto vale la energía mecánica del sistema cuando $x_{A}=L/2$, estando las dos masas en reposo?

Esfera sobre un plano inclinado con una cuerda horizontal

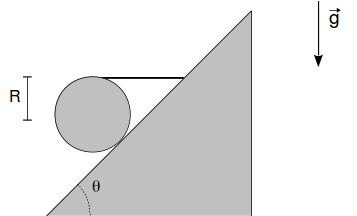
Una esfera uniforme de masa $M$ y radio $R$ se mantiene en reposo sobre un plano inclinado un ángulo $\theta$ mediante una cuerda horizontal, como se indica en la figura. El contacto entre la esfera y el plano es rugoso con coeficiente de rozamiento estático $\mu$.

1. Dibuja el diagrama de cuerpo libre de la esfera.
2. Calcula la tensión de la cuerda, la fuerza de rozamiento y la reacción del plano sobre la esfera.
3. Analiza los valores del ángulo para los cuales es posible el equilibrio.