No Boletín - Camino más corto entre un punto y una recta II (Ex.Nov/16)
Enunciado
Una partícula, cuyo vector de posición inicial es , se mueve con velocidad constante . Se observa que la distancia entre la partícula y el origen de coordenadas disminuye hasta alcanzar un valor mínimo (no nulo), y posteriormente aumenta. ¿Cuál es el vector de posición de la partícula en el instante en el que ésta tiene su mínima distancia al origen de coordenadas?
Solución
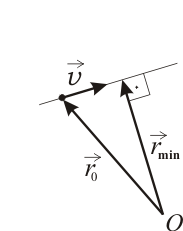
Aunque estrictamente sea de cinemática de la partícula, este ejercicio puede considerarse en la práctica como propio del álgebra de vectores libres. El movimiento de una partícula con velocidad constante es rectilíneo y, por tanto, lo que se nos pide equivale a determinar el vector que lleva desde un punto (el origen de coordenadas ) hasta una recta (la trayectoria de la partícula) por el camino más corto. La recta está definida porque conocemos un vector director de la misma (la velocidad de la partícula) y un punto por el que pasa (posición inicial de la partícula ).
Descomponiendo el vector como la suma de dos vectores: uno perpendicular a y otro paralelo a (en la teoría se ha deducido una fórmula para este tipo de descomposición), se observa que el vector buscado coincide precisamente con el vector perpendicular a de la citada descomposición:
Así pues, el vector de posición de la partícula en el instante en el que ésta tiene su mínima distancia al origen de coordenadas viene dado por la expresión:





